Next: Appendix: Examples of Use Up: Appendix: Properties of the Previous: Action on the Fourier
Let us show that, up to the degeneracy between the pairs of elements of
the basis with the same ![]() , the elements of the Fourier basis are the
only eigenfunctions of the filter operator, when it is defined within the
periodic interval. In order to do this, let us first point out that two
eigenvalues, for two different values of
, the elements of the Fourier basis are the
only eigenfunctions of the filter operator, when it is defined within the
periodic interval. In order to do this, let us first point out that two
eigenvalues, for two different values of ![]() , are never equal. We can see
this assuming that there are positive values
, are never equal. We can see
this assuming that there are positive values ![]() and
and ![]() such that
such that
Since this must stay valid for small changes of ![]() , we may
differentiate with respect to
, we may
differentiate with respect to ![]() and thus obtain
and thus obtain
This now implies that
Since ![]() and both
and both ![]() and
and ![]() are positive, we must have
are positive, we must have
Since both the cosines and the sines of the two arguments are thus seen to
be equal, it follows that the two arguments must be equal, and hence that
we must have ![]() . Therefore, the eigenvalues for two different values
of
. Therefore, the eigenvalues for two different values
of ![]() are never equal. Let us consider now an arbitrary function
are never equal. Let us consider now an arbitrary function ![]() and its expression in the Fourier basis,
and its expression in the Fourier basis,
![\begin{displaymath}
f(x)
=
\frac{1}{2}\,
\alpha_{0}
+
\sum_{k=1}^{\infty}
\left[
\alpha_{k}\cos(kx)
+
\beta_{k}\sin(kx)
\right],
\end{displaymath}](img7.png)
Let us assume that this function is not identically zero, and that it is an eigenfunction of the first-order filter operator, that is
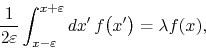
for some real number ![]() . We are therefore assuming that it is a
normalizable function that is an eigenfunction of the filter operator.
Using the expression of the function on the Fourier basis, which is
complete to represent almost everywhere any integrable real function on
the periodic interval, we get
. We are therefore assuming that it is a
normalizable function that is an eigenfunction of the filter operator.
Using the expression of the function on the Fourier basis, which is
complete to represent almost everywhere any integrable real function on
the periodic interval, we get
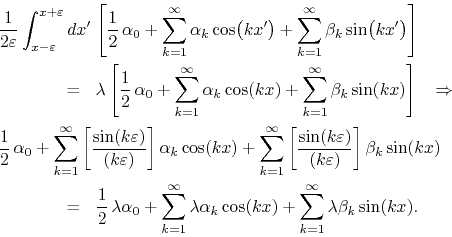
Passing all terms to the same side we may write this as the expansion of a certain function in the Fourier basis,
![\begin{displaymath}
\frac{1}{2}\,
(1-\lambda)
\alpha_{0}
+
\sum_{k=1}^{\inf...
...(k\varepsilon)}
-
\lambda
\right]
\beta_{k}\sin(kx)
=
0.
\end{displaymath}](img173.png)
This is the expansion of the null function in the Fourier basis, which is unique and therefore implies that all coefficients must be zero. We have therefore
![\begin{eqnarray*}
(1-\lambda)
\alpha_{0}
& = &
0,
\\
\left[
\frac{\sin(k...
...lon)}{(k\varepsilon)}
-
\lambda
\right]
\beta_{k}
& = &
0,
\end{eqnarray*}](img174.png)
the last two for all ![]() . Taking first the case
. Taking first the case ![]() , if
, if ![]() we
may have
we
may have
![]() , but since the other eigenvalues are never
equal to
, but since the other eigenvalues are never
equal to ![]() , we must have then
, we must have then ![]() and
and ![]() for all
for all
![]() . On the other hand, if
. On the other hand, if ![]() is equal to one of the eigenvalues
with
is equal to one of the eigenvalues
with ![]() , then it is different from all the other eigenvalues, since the
eigenvalues for two values of
, then it is different from all the other eigenvalues, since the
eigenvalues for two values of ![]() are never equal. In this case we may
have
are never equal. In this case we may
have
![]() and
and
![]() for one value of
for one value of ![]() , but
all the other coefficients must be zero. Therefore the function
, but
all the other coefficients must be zero. Therefore the function ![]() must be either a constant function or a linear combination of
must be either a constant function or a linear combination of ![]() and
and ![]() for a single value of
for a single value of ![]() .
.