Next: Critique of Perturbative Renormalization Up: Interactions Between Particles Previous: Interactions Between Particles Contents
Having discussed in sections 1.2 and 1.3 the behavior
of the
![]() model with respect to the one-point and
two-point correlation functions, which are related respectively to the
phenomena of spontaneous symmetry breaking and of the propagation of
waves and particles, we will now consider the three-point and four-point
functions, which are related to the phenomena of interaction between
waves or between particles within the model. Our first task will be to
discuss the nature of the renormalized (or physical) coupling constant
model with respect to the one-point and
two-point correlation functions, which are related respectively to the
phenomena of spontaneous symmetry breaking and of the propagation of
waves and particles, we will now consider the three-point and four-point
functions, which are related to the phenomena of interaction between
waves or between particles within the model. Our first task will be to
discuss the nature of the renormalized (or physical) coupling constant
![]() , and of its dimensionfull version
, and of its dimensionfull version ![]() , relating
them to expectation values of observables of the model. In this way we
will define these quantities and determine, at least in principle, the
way to calculate them.
, relating
them to expectation values of observables of the model. In this way we
will define these quantities and determine, at least in principle, the
way to calculate them.
As we will see, the renormalized coupling constant is a quantity that
vanishes in the Gaussian model and whose value measures how non-Gaussian
the renormalized ensemble of the model under study is, thus determining
its true degree of non-linearity and the existence or not, within the
structure of the model, of phenomena of interaction between waves or
between particles. Note that we are not talking here about the ensemble
of the fundamental field, but rather about the ensemble of the physical
variables associated to blocks, as was discussed in the section in
reference [6], since these are the variables
that are directly associated to the actual physical observables of the
theory. Hence, we should expect the quantity of greater interest in this
discussion to be the dimensionfull renormalized coupling constant
![]() , since it is the dimensionfull quantities that scale in the
correct way and thus are related to the block-variable observables, as we
saw explicitly in the case of the propagator in the section in
reference [6].
, since it is the dimensionfull quantities that scale in the
correct way and thus are related to the block-variable observables, as we
saw explicitly in the case of the propagator in the section in
reference [6].
In order to be able to write the renormalized coupling constant in terms
of observables of the model, we return to the discussion of the formalism
of the generating functionals and of the effective action, which were
introduced in the sections in references [39]
and [45]. We saw in the section in
reference [39] that the complete Green functions
![]() of
the theory in the absence of external sources can be obtained by means of
multiple functional differentiations with respect to
of
the theory in the absence of external sources can be obtained by means of
multiple functional differentiations with respect to ![]() of the
functional
of the
functional ![]() defined in the equation in
reference [41], after which one makes
defined in the equation in
reference [41], after which one makes ![]() . In
addition to this, the connected Green functions
. In
addition to this, the connected Green functions
![]() in
the presence of external sources can be obtained by means of multiple
functional differentiations with respect to
in
the presence of external sources can be obtained by means of multiple
functional differentiations with respect to ![]() of the functional
of the functional
![]() . It is in these connected functions that the true
correlations of the theory are encoded, including in the case in which we
have non-vanishing external sources. The connected two-point function was
calculated explicitly in the equation in
reference [42] and the calculation of the
corresponding three-point function was proposed in the problem in
reference [43]. In that problem, starting from
the definition of the three-point function in terms of
. It is in these connected functions that the true
correlations of the theory are encoded, including in the case in which we
have non-vanishing external sources. The connected two-point function was
calculated explicitly in the equation in
reference [42] and the calculation of the
corresponding three-point function was proposed in the problem in
reference [43]. In that problem, starting from
the definition of the three-point function in terms of ![]() ,
,
![\begin{displaymath}
\frac{\mbox{\boldmath$\mathfrak{d}$}^{3}W[j]}{\mbox{\boldmat...
...d}$}j_{2}\mbox{\boldmath$\mathfrak{d}$}j_{3}}
=g_{(c,j)1,2,3},
\end{displaymath}](img547.gif)
one shows that this functions can be written in terms of the complete three-point function as
which corresponds to the subtraction from the complete function of all
possible factorizations in terms of connected functions with a smaller
number of points. Note that we returned here to the notation of the
section in reference [39], denoting the expected
value of the field by ![]() instead of
instead of ![]() and the
dependencies on the positions
and the
dependencies on the positions ![]() of the sites by indices,
of the sites by indices,
![]() . Observe that in any
circumstances in which
. Observe that in any
circumstances in which
![]() , which naturally implies that
, which naturally implies that
![]() , we have for this connected function
, we have for this connected function
![]() ,
which makes the definition of the renormalized coupling constant
considerably simpler in models based on three-point interactions, as is
the case, for example, for electrodynamics.
,
which makes the definition of the renormalized coupling constant
considerably simpler in models based on three-point interactions, as is
the case, for example, for electrodynamics.
However, the polynomial models of scalar fields, such as the
![]() model that we are studying here, are based on
interactions involving four or more points, so that we must go at least
up to the four-point function in order to be able to define the
renormalized coupling constant. It is necessary, therefore, to take a
fourth and last derivative of
model that we are studying here, are based on
interactions involving four or more points, so that we must go at least
up to the four-point function in order to be able to define the
renormalized coupling constant. It is necessary, therefore, to take a
fourth and last derivative of ![]() (problem 3.1.1),
which results, after a long but straightforward algebraic calculation, in
a relation between the connected four-point function and the
corresponding complete function,
(problem 3.1.1),
which results, after a long but straightforward algebraic calculation, in
a relation between the connected four-point function and the
corresponding complete function,
As was the case for the three-point function, this time we also obtain,
as one can see, the subtraction from the complete function of all the
possible factorizations in terms of connected functions with a smaller
number of points. The expression consists of a relatively small number of
terms with different structures, each one accompanied of all the possible
permutations of the position indices. Observe that in any circumstances
in which
![]() , corresponding necessarily to
, corresponding necessarily to ![]() , we obtain
a much simpler relation, that can be written as
, we obtain
a much simpler relation, that can be written as
since for ![]() we have that
we have that
![]() . Just as
. Just as ![]() gives us the true two-point correlations,
gives us the true two-point correlations,
![]() gives us the
true four-point correlations of the model, that is, those which are not
just superpositions of two-point correlations. While the two-point
function is related to the propagation of waves and particles, the
four-point function is related to the interaction between these waves and
between these particles. It gives us the part of the complete four-point
function which is not just a product of two-point functions. The part of
the complete four-point function that can be decomposed into such a
product of two-point functions corresponds to two waves or particles
propagating together in a region of space-time, but that superpose
linearly, passing transparently through each other, without interacting
with one another. This is in fact all that happens in the theory of the
free scaler field. One can show (problem 3.1.2) that
in that theory, where everything is linear, the connected four-point
function vanishes identically, a fact which corresponds to the lack of
interactions between waves or between particles in that theory.
gives us the
true four-point correlations of the model, that is, those which are not
just superpositions of two-point correlations. While the two-point
function is related to the propagation of waves and particles, the
four-point function is related to the interaction between these waves and
between these particles. It gives us the part of the complete four-point
function which is not just a product of two-point functions. The part of
the complete four-point function that can be decomposed into such a
product of two-point functions corresponds to two waves or particles
propagating together in a region of space-time, but that superpose
linearly, passing transparently through each other, without interacting
with one another. This is in fact all that happens in the theory of the
free scaler field. One can show (problem 3.1.2) that
in that theory, where everything is linear, the connected four-point
function vanishes identically, a fact which corresponds to the lack of
interactions between waves or between particles in that theory.
In order to relate this function with the renormalized coupling constant
we must go back to the discussion of the concept of the effective action,
which was introduced in the section in
reference [39] and discussed in detail in the
section in reference [45]. The renormalized
coupling constant is one of the parameters that appears in the expression
of the effective action, it is the parameter that relates most directly
to the connected four-point function and that encodes in the most concise
way the structure of interactions of the theory. As we saw, the effective
action
![]() is a functional of
is a functional of ![]() defined
from
defined
from ![]() by a Legendre transformation. As we saw in the equation in
reference [47], the double functional
derivative of
by a Legendre transformation. As we saw in the equation in
reference [47], the double functional
derivative of
![]() with respect to
with respect to ![]() is
related to the inverse of the propagator. Starting from that equation we
may write, with some changes of indices and an additional sum over the
lattice, the equation
is
related to the inverse of the propagator. Starting from that equation we
may write, with some changes of indices and an additional sum over the
lattice, the equation
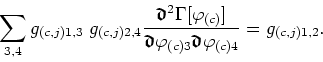
If we differentiate this once more with respect to ![]() , using then the
chain rule in order to rewrite the derivatives as derivatives with
respect to
, using then the
chain rule in order to rewrite the derivatives as derivatives with
respect to ![]() , as we did in the derivation of the equation
in reference [47], and recalling also that the
double functional derivative of
, as we did in the derivation of the equation
in reference [47], and recalling also that the
double functional derivative of
![]() is the inverse of
the propagator, we obtain (problem 3.1.3)
is the inverse of
the propagator, we obtain (problem 3.1.3)
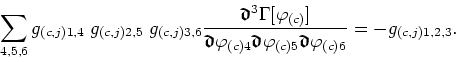
This shows that the triple functional derivative of
![]() is related to the three-point connected
function. We can see that the connected three-point function is obtained
from the triple functional derivative of
is related to the three-point connected
function. We can see that the connected three-point function is obtained
from the triple functional derivative of
![]() by means
of a type of triple transformation in which the transformation function
is the propagator. In a diagrammatic language, we can say that the triple
functional derivative is a vertex to which are connected three external legs representing the three propagators that act as
transformation functions, this whole set of elements being equivalent to
the connected three-point function. This is therefore a new type of
decomposition, a way of decomposing the connected three-point function
into simpler, more fundamental parts. These simpler parts are denominated
one-particle irreducible or ``1pi'' functions. The corresponding
diagram is illustrated in figure 3.1.1. If we
differentiate this expression a fourth and last time, using the same
techniques and ideas, we obtain, after long algebraic passages
(problem 3.1.4), the relation
by means
of a type of triple transformation in which the transformation function
is the propagator. In a diagrammatic language, we can say that the triple
functional derivative is a vertex to which are connected three external legs representing the three propagators that act as
transformation functions, this whole set of elements being equivalent to
the connected three-point function. This is therefore a new type of
decomposition, a way of decomposing the connected three-point function
into simpler, more fundamental parts. These simpler parts are denominated
one-particle irreducible or ``1pi'' functions. The corresponding
diagram is illustrated in figure 3.1.1. If we
differentiate this expression a fourth and last time, using the same
techniques and ideas, we obtain, after long algebraic passages
(problem 3.1.4), the relation
This relation has an interesting diagrammatic representation, which we
illustrate in figure 3.1.2, where the symbol
![]() represents the inverse of the propagator, as defined in the
equation in reference [48]. The last three
parts of this diagram correspond to all the possible ways to build a
four-point process with the connected three-point functions and at most a
single internal
represents the inverse of the propagator, as defined in the
equation in reference [48]. The last three
parts of this diagram correspond to all the possible ways to build a
four-point process with the connected three-point functions and at most a
single internal
![]() . We see therefore that the left side of the
equation corresponds to the difference between the connected four-point
function and these constructions. It is due to this that the functions
generated directly by
. We see therefore that the left side of the
equation corresponds to the difference between the connected four-point
function and these constructions. It is due to this that the functions
generated directly by
![]() are called ``one-particle
irreducible'' or ``1pi'', that is, they are irreducible functions in the
sense that they cannot be separated into other functions by the
elimination of an internal line of the corresponding the diagram. In
somewhat more physical terms, the 1pi four-point function is the part of
the four-point interaction that cannot be built out of two three-point
interactions. The dimensionless versions of these 1pi functions will be
denoted by
are called ``one-particle
irreducible'' or ``1pi'', that is, they are irreducible functions in the
sense that they cannot be separated into other functions by the
elimination of an internal line of the corresponding the diagram. In
somewhat more physical terms, the 1pi four-point function is the part of
the four-point interaction that cannot be built out of two three-point
interactions. The dimensionless versions of these 1pi functions will be
denoted by ![]() , with position variables as arguments,
, with position variables as arguments,
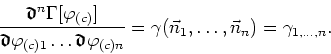
These functions are also referred to as truncated, meaning that the
propagators corresponding to the external legs are absent from the
functions
![]() . It is for this reason that they are also
called ``vertices'', meaning that they represent only the central
vertices that connect together the external legs of the diagrams, without
the inclusion of the external legs themselves. All this diagrammatic
nomenclature is mentioned here only to make contact with what one sees in
the more traditional ways to approach the theory, since it will not have
much importance for our approach in these notes.
. It is for this reason that they are also
called ``vertices'', meaning that they represent only the central
vertices that connect together the external legs of the diagrams, without
the inclusion of the external legs themselves. All this diagrammatic
nomenclature is mentioned here only to make contact with what one sees in
the more traditional ways to approach the theory, since it will not have
much importance for our approach in these notes.
For models with ![]() and in which there is symmetry by the reflection of
the fields, not only we have
and in which there is symmetry by the reflection of
the fields, not only we have
![]() but the symmetry also
implies that all the functions with an odd number of points vanish. In
particular,
but the symmetry also
implies that all the functions with an odd number of points vanish. In
particular,
![]() and there are, therefore, no three-point
interactions. In this case equation (3.1.3) can
be simplified to
and there are, therefore, no three-point
interactions. In this case equation (3.1.3) can
be simplified to
It is clear that the four-fold functional derivative has the effect of
extracting from the quartic term of
![]() its
coefficient, which will be proportional to the renormalized coupling
constant. Therefore, the last step we must take in this sequence of
calculations it to isolate
its
coefficient, which will be proportional to the renormalized coupling
constant. Therefore, the last step we must take in this sequence of
calculations it to isolate
![]() in the relation above
between this 1pi functions and the connected correlation function
in the relation above
between this 1pi functions and the connected correlation function
![]() , which we already know how to write directly in terms of
expectation values of products of the fields. In order to do this we will
rewrite this equation in momentum space, performing Fourier transforms on
the four variables
, which we already know how to write directly in terms of
expectation values of products of the fields. In order to do this we will
rewrite this equation in momentum space, performing Fourier transforms on
the four variables
![]() which are not added
over. Taking the four-fold Fourier transform of
equation (3.1.4) and using the discrete
translation invariance of the lattice
(problem 3.1.5), we obtain
which are not added
over. Taking the four-fold Fourier transform of
equation (3.1.4) and using the discrete
translation invariance of the lattice
(problem 3.1.5), we obtain
where we are denoting the momentum coordinates by indices and where
![]() is the momentum-space propagator,
which depends on only a single momentum coordinate, due to the discrete
translation invariance. Since the propagators in momentum space are never
zero, we may now isolate the 1pi function, writing it as
is the momentum-space propagator,
which depends on only a single momentum coordinate, due to the discrete
translation invariance. Since the propagators in momentum space are never
zero, we may now isolate the 1pi function, writing it as
We have here the 1pi function written in terms of expectation values of the model in momentum space.
In order to relate this to the renormalized coupling constant, we will
have to make some assumptions about the form that the effective action
![]() may have, which will be based on the symmetries
of the model. Let us recall then that our polynomial model is defined by
the action given in equation (1.1.1), which
we reproduce here,
may have, which will be based on the symmetries
of the model. Let us recall then that our polynomial model is defined by
the action given in equation (1.1.1), which
we reproduce here,
![\begin{displaymath}
S[\varphi]=\frac{1}{2}\sum_{\ell}(\Delta_{\ell}\varphi)^{2}
...
...um_{s}\varphi^{2}(s)
+\frac{\lambda}{4}\sum_{s}\varphi^{4}(s).
\end{displaymath}](img348.gif)
We will be interested primarily in analyzing the low-momentum regime of the model, because this is enough for obtaining the value of the renormalized coupling constant, since it appears as part of a local potential, which exists even for fields which are constant over the lattice, having therefore infinite wavelength and vanishing momenta. In addition to this, we will assume that the effective action has the same symmetries that the fundamental action which defines the model has. Naturally, at this point it is necessary to consider for a while the issue of the possibility of spontaneous symmetry breaking that we know to exist in this model.
Let us recall that on finite lattices the symmetry is always broken, with
![]() . If we introduce into the model an infinitesimal constant
external source
. If we introduce into the model an infinitesimal constant
external source ![]() , the field will spontaneously orient itself in
the direction of the external source, be it positive or negative, without
the system presenting any resistance to this change. For a sufficiently
small
, the field will spontaneously orient itself in
the direction of the external source, be it positive or negative, without
the system presenting any resistance to this change. For a sufficiently
small ![]() , this happens without any significant change in the
``energy'' (in fact, the action) of the system, so that the effective potential of the theory, the part of the effective action that
does not involve derivatives of
, this happens without any significant change in the
``energy'' (in fact, the action) of the system, so that the effective potential of the theory, the part of the effective action that
does not involve derivatives of ![]() , must be completely flat
in a region around the point
, must be completely flat
in a region around the point
![]() , as
figure 3.1.3 illustrates. We use in this
figure the quantity
, as
figure 3.1.3 illustrates. We use in this
figure the quantity ![]() without arguments as the value of
without arguments as the value of
![]() for
for
![]() by positive values. Both
by positive values. Both
![]() and
and ![]() are renormalized parameters that are
related to the form of the graph of the effective potential in the
regions
are renormalized parameters that are
related to the form of the graph of the effective potential in the
regions
![]() and
and
![]() .
.
If we rewrite the effective potential in terms of the shifted classical
field
![]() , recalling that
, recalling that ![]() changes sign when
changes sign when ![]() changes sign, then we can represent the
effective potential as shown in figure 3.1.4.
Observe that in the continuum limit we have
changes sign, then we can represent the
effective potential as shown in figure 3.1.4.
Observe that in the continuum limit we have
![]() , since
it is necessary that we approach the critical curve in the limit, where
, since
it is necessary that we approach the critical curve in the limit, where
![]() since the phase transition is second-order. Hence, if we will
end up by taking the limit, we can do the analysis either in terms of
since the phase transition is second-order. Hence, if we will
end up by taking the limit, we can do the analysis either in terms of
![]() or in terms of
or in terms of ![]() . For simplicity, we will
limit ourselves here to the derivation of the relation between
. For simplicity, we will
limit ourselves here to the derivation of the relation between
![]() and the observables of the model in the case in which
and the observables of the model in the case in which
![]() , but it is not difficult to generalize the result
(problem 3.1.6).
, but it is not difficult to generalize the result
(problem 3.1.6).
Since we will assume that the effective action, when written in terms of
![]() , has the same symmetries that the fundamental action
which defines the model has, it follows that
, has the same symmetries that the fundamental action
which defines the model has, it follows that
![]() must be composed of terms that have the same symmetries of the terms
existing in
must be composed of terms that have the same symmetries of the terms
existing in ![]() , that is, that it must have the general form
, that is, that it must have the general form
![\begin{displaymath}
\Gamma[\varphi'_{(c)}]=\frac{1}{\zeta}\left\{
\frac{1}{2}\su...
...}}{4}\sum_{s}\varphi'^{4}_{(c)}(s) +\mbox{ (others)
}\right\},
\end{displaymath}](img596.gif)
where we wrote explicitly the terms which are relevant for the analysis
of the low-momentum regime of the model, ![]() is the residue of the
pole of the propagator and ``others'' indicates terms with more than four
powers of the field and terms with more than two derivatives. Terms with
many derivatives do not contribute significantly to the low-momentum
regime and terms with more than four powers of the field do not
contribute to the four-point function. Based on the numerical experience
with this model, we may assume that
is the residue of the
pole of the propagator and ``others'' indicates terms with more than four
powers of the field and terms with more than two derivatives. Terms with
many derivatives do not contribute significantly to the low-momentum
regime and terms with more than four powers of the field do not
contribute to the four-point function. Based on the numerical experience
with this model, we may assume that ![]() , which seems to be true
with significant precision in all cases examined so far.
, which seems to be true
with significant precision in all cases examined so far.
When taking the functional derivatives of
![]() , and
considering that we are interested in the case
, and
considering that we are interested in the case ![]() , we should realize
that it is implicit that we should put
, we should realize
that it is implicit that we should put
![]() at the end of
the calculations, because this is the value of
at the end of
the calculations, because this is the value of
![]() that
corresponds to the condition
that
corresponds to the condition ![]() in this model. It is clear that the
quadratic terms will vanish anyway when we take the derivatives, while
the terms with powers larger than four will vanish due to the condition
in this model. It is clear that the
quadratic terms will vanish anyway when we take the derivatives, while
the terms with powers larger than four will vanish due to the condition
![]() . Therefore, we may consider only the terms of the
effective action that contain exactly four powers of the field and no
derivatives, and so we are reduced to considering only the term
. Therefore, we may consider only the terms of the
effective action that contain exactly four powers of the field and no
derivatives, and so we are reduced to considering only the term
![\begin{displaymath}
V_{(4)}[\varphi'_{(c)}]=\frac{\lambda_{R}}{4}\sum_{0}\varphi'^{4}_{(c)0},
\end{displaymath}](img599.gif)
which is the term of the effective potential which is relevant for zero momentum. Taking the first derivative we get
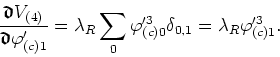
Multiplying this equation by ![]() , where, in order to simplify the
notation, we are denoting the mode functions of the Fourier basis as
, where, in order to simplify the
notation, we are denoting the mode functions of the Fourier basis as
then adding over the variable ![]() and differentiating a second
time we get
and differentiating a second
time we get
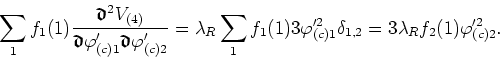
Multiplying now by ![]() , adding over the variable
, adding over the variable ![]() and
differentiating a third time we get
and
differentiating a third time we get
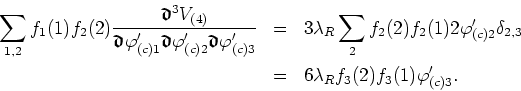
Repeating the procedure a fourth and last time we get
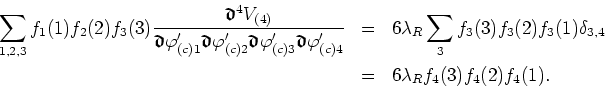
Multiplying by ![]() and adding over
and adding over ![]() we obtain for the
fourth functional derivative of
we obtain for the
fourth functional derivative of ![]()
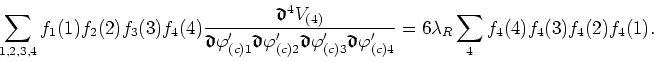
Since this fourth functional derivative is equal to the 1pi four-point function, we obtain
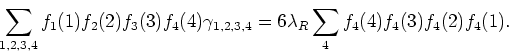
In the left-hand side of this equation we have ![]() times the
four-fold Fourier transform of
times the
four-fold Fourier transform of
![]() , while in the
right-hand side, recalling that the mode functions
, while in the
right-hand side, recalling that the mode functions ![]() are
exponentials that satisfy orthogonality and completeness relations, we
have
are
exponentials that satisfy orthogonality and completeness relations, we
have ![]() times a Kronecker delta function that expresses the
conservation of momentum, that is,
times a Kronecker delta function that expresses the
conservation of momentum, that is,
Combining now this equation with equation (3.1.5) we obtain the final relation between the renormalized coupling constant and the connected correlation functions,
For combinations of momenta that satisfy the conservation condition
![]() the delta
function is simply
the delta
function is simply ![]() and, assuming implicitly the conservation of
momentum, we may write
and, assuming implicitly the conservation of
momentum, we may write
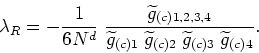
Naturally, since we neglected the terms in
![]() with
larger powers of the momenta, this relation only makes sense for small or
vanishing momenta. We take, therefore, the zero-momentum case
with
larger powers of the momenta, this relation only makes sense for small or
vanishing momenta. We take, therefore, the zero-momentum case
![]() in order to
obtain, substituting the connected functions in terms of the complete
functions,
in order to
obtain, substituting the connected functions in terms of the complete
functions,
If we recall the factorization relations of the free theory for the correlation functions in momentum space, that were introduced in the section of reference [44], we immediately see that this quantity vanishes identically in the free theory.
We may also write this result in terms of the dimensionfull quantities,
using the appropriate scaling relations to transform ![]() in
in ![]() and
and ![]() in
in ![]() , thus obtaining
, thus obtaining
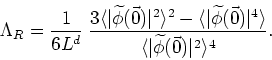
This is the quantity whose value determines whether or not there exists in this model the phenomenon of non-linear interaction between waves, or between particles. Naturally, this quantity is of great physical interest and we will dedicate some time to the examination of its properties.
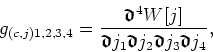
in a theory with a non-vanishing external source ![]() , show that it is
related to the complete functions of four, three and two points by the
formula
, show that it is
related to the complete functions of four, three and two points by the
formula
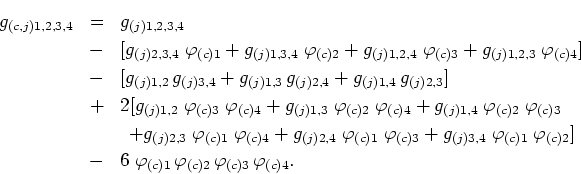
Substituting the complete functions of three and two points in terms of the corresponding connected functions, show that the connected four-point function is related to the complete four-point function by means of
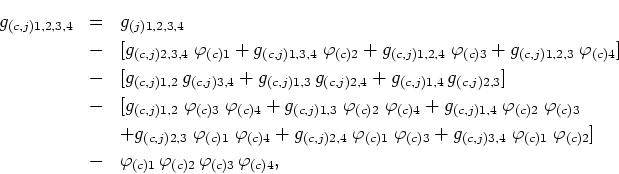
which corresponds to the subtraction from the complete function of all the possible factorizations in terms of connected functions with a smaller number of points.
Observe that a significant part of the long algebraic passages involved in this problem has already been executed before in the problem in reference [40], relative to the three-point function. A simpler alternative way to obtain the results shown above is to start from the final result of that problem, doing an additional differentiation and using once more the same result to substitute the complete three-point function where necessary.
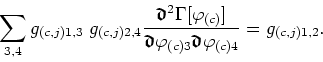
Then differentiate this equation once more with respect to ![]() , using the
chain rule to rewrite the derivatives as derivatives with respect to
, using the
chain rule to rewrite the derivatives as derivatives with respect to
![]() , thus obtaining
, thus obtaining
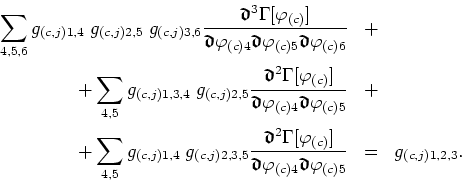
Next, use the fact that the second functional derivative of
![]() is the inverse of the propagator and rearrange
the terms in order to obtain the final relation in the form
is the inverse of the propagator and rearrange
the terms in order to obtain the final relation in the form
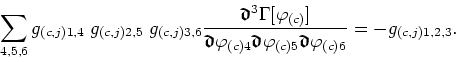
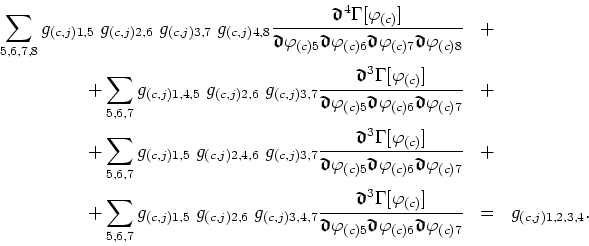
Using again the final result of problem 3.1.3
and, once more, the fact that the second functional derivative of
![]() is the inverse of the propagator, obtain the
final relation
is the inverse of the propagator, obtain the
final relation
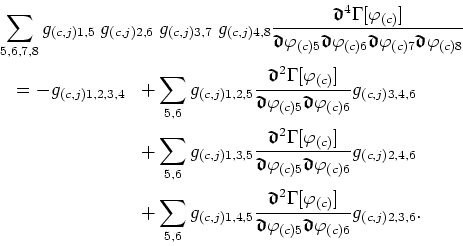
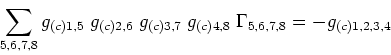
and execute four Fourier transforms on the external variables
![]() , using the corresponding variables
, using the corresponding variables
![]() in momentum space, and recalling that,
for a function
in momentum space, and recalling that,
for a function ![]() of
of ![]() position variables
position variables ![]() ,
,
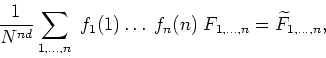
where, to simplify the notation, we are denoting the mode functions of the Fourier basis as
besides indicating the momentum coordinates by indices on the remaining functions in momentum space, as we have done before for the position coordinates. Use also the fact that, due to the discrete translation invariance of the lattice, we have
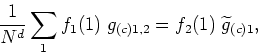
where
![]() is the propagator in momentum space, which depends
only on a single momentum coordinate, due the the discrete translation
invariance, in order to write the final result
is the propagator in momentum space, which depends
only on a single momentum coordinate, due the the discrete translation
invariance, in order to write the final result
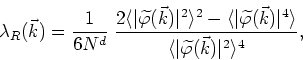
both in the case in which ![]() and
and ![]() and in the general case.
and in the general case.