Next: Spontaneous Symmetry Breaking Up: The Polynomial Model Previous: Definition of the Model Contents
In this section we will develop in detail a perturbative approximation
technique for the
![]() model which we introduced in
section 1.1. As we shall see later on, it will allow us to
confirm the qualitative behavior of the model, which was described in a
heuristic way in that section. Let us recall that the model is defined by
the action
model which we introduced in
section 1.1. As we shall see later on, it will allow us to
confirm the qualitative behavior of the model, which was described in a
heuristic way in that section. Let us recall that the model is defined by
the action
![\begin{displaymath}
S[\varphi]=\frac{1}{2}\sum_{\ell}(\Delta_{\ell}\varphi)^{2}
...
...um_{s}\varphi^{2}(s)
+\frac{\lambda}{4}\sum_{s}\varphi^{4}(s),
\end{displaymath}](img22.gif)
containing a quartic interaction term. Due to the presence of the quartic
term we do not know how to solve the model analytically. However, without
this term the model becomes Gaussian and then we are able to solve it
completely. It becomes clear then that the results of the complete model
should converge to the corresponding results of the free theory when we
make
![]() since, in the continuum limit, this implies
that we must approach the Gaussian point in the parameter plane of the
model.
since, in the continuum limit, this implies
that we must approach the Gaussian point in the parameter plane of the
model.
The main idea of perturbation theory is to develop an expansion for the complete model around the soluble Gaussian model. Presumably, for small values of the coupling constant the results of the complete model are not very different from the results of the free theory and hence we may understand the interaction term as a small perturbation applied to the Gaussian model. In this way, maybe we will be able to use the expansion in order to obtain useful approximations for the complete model near the Gaussian point in the critical diagram. This is just the usual expectation that one has for an approximation scheme, but a word of warning is in order here. Although we will see that it is in fact possible to calculate some useful approximations, things are not as simple as one may think at first, and the approximation scheme does not work quite in the way that one would expect.
The first step in the development of the perturbative technique is the
separation of the action in two parts, which we shall denominate ![]() and
and ![]() ,
,
where ![]() is a purely Gaussian action. For the time being we will not
be very specific about the detailed form of each one of the two parts. We
have, for an arbitrary observable
is a purely Gaussian action. For the time being we will not
be very specific about the detailed form of each one of the two parts. We
have, for an arbitrary observable ![]() of the complete model,
of the complete model,
We may now write this in terms of the measure of the free theory defined
by ![]() , dividing both numerator and denominator by
, dividing both numerator and denominator by
![]() and thus obtaining
and thus obtaining
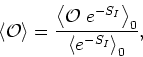
where the subscript ![]() denotes expectation values of the theory defined
by
denotes expectation values of the theory defined
by ![]() ,
,
![\begin{displaymath}
\langle{\cal O}\rangle_{0}=\frac{\displaystyle \int[{\bf d}\...
...phi]e^{-S_{0}}}{\displaystyle \int[{\bf d}\varphi]e^{-S_{0}}}.
\end{displaymath}](img148.gif)
The term ![]() of the action is the one that contains the parameter
of the action is the one that contains the parameter
![]() , that we presume to be small. However, in general
, that we presume to be small. However, in general ![]() may
contain also other parameters, so that in order to enable us to do the
development of the perturbation theory in a more organized and explicit
fashion it is convenient to use, instead of
may
contain also other parameters, so that in order to enable us to do the
development of the perturbation theory in a more organized and explicit
fashion it is convenient to use, instead of ![]() , a new expansion
parameter
, a new expansion
parameter ![]() that we introduce as follows,
that we introduce as follows,
We have therefore that
![]() and
and
![]() . Perturbation theory consists of making a series
expansion, which we denominate the perturbative expansion, of
. Perturbation theory consists of making a series
expansion, which we denominate the perturbative expansion, of
![]() around
around ![]() , up to a certain order, followed
by the use of the resulting expressions at the point
, up to a certain order, followed
by the use of the resulting expressions at the point ![]() . Of
course this can only be a good approximation to the complete theory if
. Of
course this can only be a good approximation to the complete theory if
![]() is a small quantity. Classically we can make
is a small quantity. Classically we can make ![]() small by
adjusting the values of
small by
adjusting the values of ![]() and any other parameters that it may
contain but, as we shall see in what follows, this is not possible
in the quantum theory. This is the basic fact that is at the root of all
difficulties with the perturbative approach to quantum field theory.
and any other parameters that it may
contain but, as we shall see in what follows, this is not possible
in the quantum theory. This is the basic fact that is at the root of all
difficulties with the perturbative approach to quantum field theory.
In order to understand the origin of the difficulties it is necessary to
recall some important properties of the theory of the free scalar field,
since we are writing our quantities here in terms of the expectation
values of that theory. As we saw in the section
in [7], in the case of the dimensions ![]() which are the ones of interest for quantum field theory, the quantity
which are the ones of interest for quantum field theory, the quantity
![]() , which we denote here by
, which we denote here by
![]() to record the fact that it is a quantity relating to the
free theory, is a finite and non-zero quantity both on finite lattices
and in the continuum limit. In addition to this, we showed in the section
in [8] that the quantity
to record the fact that it is a quantity relating to the
free theory, is a finite and non-zero quantity both on finite lattices
and in the continuum limit. In addition to this, we showed in the section
in [8] that the quantity
![]() is also finite and non-zero
both on finite lattices and in the limit, in which case it has the value
is also finite and non-zero
both on finite lattices and in the limit, in which case it has the value
![]() . Still in the section in [8] these facts
were used to show that both the expectation value of the kinetic part
. Still in the section in [8] these facts
were used to show that both the expectation value of the kinetic part
![]() of the action,
of the action,
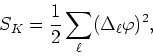
and the expectation value of the part ![]() of the action containing
the mass term,
of the action containing
the mass term,
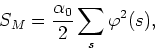
diverge as powers of ![]() in the continuum limit, even if we keep the
models within boxes with finite volumes. In the case of
in the continuum limit, even if we keep the
models within boxes with finite volumes. In the case of ![]() we have
we have
![]() , while in the case of
, while in the case of ![]() we have
we have
![]() . In addition
to this, it is possible to show that in the free theory the following
relation holds,
. In addition
to this, it is possible to show that in the free theory the following
relation holds,
which is the result indicated in the problem
in [9]. From these consideration it follows
that, assuming that the general form of ![]() is given by
is given by ![]() ,
,
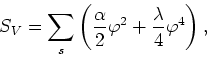
where ![]() , we have for its expectation value
, we have for its expectation value
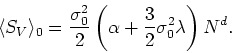
This means that, so long as the factor within parenthesis is not zero in
the limit,
![]() diverges as
diverges as ![]() in the continuum
limit.
in the continuum
limit.
At first sight it may seem that the expression in parenthesis may indeed
vanish in the limit, since we must remember that, as was discussed in
section 1.1, ![]() is necessarily negative in the limit,
while the factors contained in the second term of the expression are all
positive. In fact, this expression is similar to our heuristic estimate
for the equation of the critical curve, which was
is necessarily negative in the limit,
while the factors contained in the second term of the expression are all
positive. In fact, this expression is similar to our heuristic estimate
for the equation of the critical curve, which was
![]() . However, one can verify
a-posteriori that the expression is not identical to the equation of the
critical curve, either by numerical means or by the the approximations in
which we will calculate the equation of the curve later on. For example,
in the case of the perturbative approximation we will verify that the two
expressions differ by the extra factor of
. However, one can verify
a-posteriori that the expression is not identical to the equation of the
critical curve, either by numerical means or by the the approximations in
which we will calculate the equation of the curve later on. For example,
in the case of the perturbative approximation we will verify that the two
expressions differ by the extra factor of ![]() that appears in the
second term in the parenthesis in the expression of
that appears in the
second term in the parenthesis in the expression of
![]() .
.
In any case, even if the expression in parenthesis did coincide with the
equation of the critical line, it would not be equal to zero on finite
lattices, but would only approach zero in the
![]() limit,
with some inverse power of
limit,
with some inverse power of ![]() . Since the expression is multiplied by a
factor of
. Since the expression is multiplied by a
factor of ![]() , it would have to go to zero very fast in order to
avoid the divergence. As we saw in section 1.1 and will confirm
quantitatively later on, the equation of the critical curve is directly
related to the value of
, it would have to go to zero very fast in order to
avoid the divergence. As we saw in section 1.1 and will confirm
quantitatively later on, the equation of the critical curve is directly
related to the value of ![]() , so that it must go to zero exactly
as
, so that it must go to zero exactly
as ![]() , which is not enough to eliminate the divergence in the
dimensions of interest,
, which is not enough to eliminate the divergence in the
dimensions of interest, ![]() . Furthermore, even if everything worked
out and
. Furthermore, even if everything worked
out and
![]() did go to zero in the limit, if we
consider that we also have that
did go to zero in the limit, if we
consider that we also have that
![]() diverges as
diverges as
![]() in the limit, we see that the resulting theory could not possibly
fail to become trivial in that case, since the interaction term would
then become vanishingly small in the continuum limit, when compared to
the remaining part of the action.
in the limit, we see that the resulting theory could not possibly
fail to become trivial in that case, since the interaction term would
then become vanishingly small in the continuum limit, when compared to
the remaining part of the action.
The conclusion to which we are forced is that
![]() in
fact diverges in the continuum limit as
in
fact diverges in the continuum limit as ![]() . It is important to
observe once more that this divergence is not due to an integration over
an infinite volume, because we can do the complete development of the
theory within a finite box without any change in this result. This
divergence is a property of the continuum limit, an ultraviolet
characteristic of the theory, in which the influence of the
high-frequency and short-wavelength modes of momentum space predominate.
It is not a property of the infinite-volume limit, that is, of the
infrared regime of the theory, in which the low-frequency and
long-wavelength modes predominate. It becomes clear, therefore, that it
is not possible to keep
. It is important to
observe once more that this divergence is not due to an integration over
an infinite volume, because we can do the complete development of the
theory within a finite box without any change in this result. This
divergence is a property of the continuum limit, an ultraviolet
characteristic of the theory, in which the influence of the
high-frequency and short-wavelength modes of momentum space predominate.
It is not a property of the infinite-volume limit, that is, of the
infrared regime of the theory, in which the low-frequency and
long-wavelength modes predominate. It becomes clear, therefore, that it
is not possible to keep ![]() small by mere changes in the parameters
small by mere changes in the parameters
![]() and
and ![]() , except if we make them converge rapidly to zero
in the continuum limit, which takes us back to the Gaussian point, where
all the results are already known, constituting the theory of the free
scalar field.
, except if we make them converge rapidly to zero
in the continuum limit, which takes us back to the Gaussian point, where
all the results are already known, constituting the theory of the free
scalar field.
At this point it does not seem that this perturbative technique can end up having any practical use but, in any case, let us proceed with our analysis of the situation. If we consider for a moment the denominator of equation (1.2.1) it is clear that we will have, in the continuum limit,
while the perturbative expansion of this quantity, obtained by the series
expansion of the exponential function, will contain divergent terms if we
keep ![]() finite and non-zero when we take the limit,
finite and non-zero when we take the limit,
We see here that a simple and naive expansion within such a singular
structure can make a vanishing quantity appear as a collection of
infinities in the terms of the expansion. We can now see that the limit
of equation (1.2.1) for
![]() is a
limit of the form
is a
limit of the form ![]() . However, it certainly exists, so long as the
theory is well defined, which we expect to be true so long as we keep the
parameters of the theory within the stable region of the critical
diagram. The denominator can be understood as the ratio of the measures
of the interacting model and of the free theory,
. However, it certainly exists, so long as the
theory is well defined, which we expect to be true so long as we keep the
parameters of the theory within the stable region of the critical
diagram. The denominator can be understood as the ratio of the measures
of the interacting model and of the free theory,
![\begin{displaymath}
\left\langle e^{-S_{I}}\right\rangle_{0}=\frac{\displaystyle...
...(S_{0}+S_{I})}}{\displaystyle \int[{\bf d}\varphi]e^{-S_{0}}},
\end{displaymath}](img180.gif)
so that the conclusion we arrive at is that these two measures are
related in a singular way in the continuum limit. On any finite lattice
the expectation value
![]() is finite and we can
improve the approximation by decreasing somewhat the parameters
is finite and we can
improve the approximation by decreasing somewhat the parameters ![]() and
and ![]() . However, in the continuum limit the only form to avoid the
divergence is to make both
. However, in the continuum limit the only form to avoid the
divergence is to make both ![]() and
and ![]() approach zero very
quickly, thus making the model return to the Gaussian point.
approach zero very
quickly, thus making the model return to the Gaussian point.
This behavior of ![]() is the basic cause that is behind all the
divergences that appear in the perturbative expansion of the model. It is
directly related to the strong fluctuations undergone by the fields in
the continuum limit, as well as with the fact that the dominating field
configuration are discontinuous in the limit, as we studied in the
section in [8]. Despite all this, it is still
very reasonable to think that the observables
is the basic cause that is behind all the
divergences that appear in the perturbative expansion of the model. It is
directly related to the strong fluctuations undergone by the fields in
the continuum limit, as well as with the fact that the dominating field
configuration are discontinuous in the limit, as we studied in the
section in [8]. Despite all this, it is still
very reasonable to think that the observables
![]() of the
complete model are continuous functions of the parameters of the model,
because the observables are defined by means of statistical averages that
eliminate the fluctuations and discontinuities which are characteristic
of the fundamental field. In other words, it is reasonable to think that
of the
complete model are continuous functions of the parameters of the model,
because the observables are defined by means of statistical averages that
eliminate the fluctuations and discontinuities which are characteristic
of the fundamental field. In other words, it is reasonable to think that
![]() is at least a continuous and differentiable function of
is at least a continuous and differentiable function of
![]() , so that there should be at least a reasonable first-order
approximation for
, so that there should be at least a reasonable first-order
approximation for ![]() near
near ![]() , and it could even be that
, and it could even be that ![]() is an analytical function of
is an analytical function of ![]() (problem 1.2.1).
(problem 1.2.1).
We are faced here by a rather strange situation: on the one hand, it is reasonable to think that there is an approximation up to some order for the observables of the complete model in the vicinity of the Gaussian point but, on the other hand, we see that this approximation may not be accessible by means of the perturbative expansion starting from the definition of the quantum theory, due to the divergences that appear. Observe that this apparent conflict is related to a exchange of order of two limits, involving the continuum limit and the limit of the summation of the perturbative series. We may argue that on finite lattices the perturbative series can be summed, since all the quantities involved are finite and well-behaved in this case. Hence, in principle we may sum the perturbative series on finite lattices and after that take the continuum limit. However, when we write the series only up to a certain term of finite order and then take the continuum limit, we are inverting the order of the two limits. Although it is reasonable to think that, once the continuum limit is taken, the resulting observables should have convergent expansions in terms of the parameters of the model, there is no guarantee that these expansions are those obtained by the exchange of the order of the limits. In fact, the divergences that appear show us that the two procedures must have very different results.
At this point it is important to observe that the
equation (1.2.1) which defines the observables of
the quantum theory is a ratio of two quantities involving ![]() and
that, due to this, it is possible that some or even all the divergences
due to this quantity end up by cancelling each other, between those
coming from the numerator and those coming from the denominator, if we
make a careful expansion of the ratio, that is, a careful expansion of
and
that, due to this, it is possible that some or even all the divergences
due to this quantity end up by cancelling each other, between those
coming from the numerator and those coming from the denominator, if we
make a careful expansion of the ratio, that is, a careful expansion of
![]() . We will verify later on that it is indeed possible to
obtain in this way a useful approximation for some of the observables of
the complete model, despite the divergences that are involved in the
limit, but we should keep in mind that we are dealing with a singular
expansion, so that it should come as no surprise it not everything works
out perfectly as expected. It is in this context that the idea of renormalization appears for the first time with a recognizable meaning.
Unfortunately, this term is used for several different things in the
structure of the theory, but here it really has to do with renormalizing
something in the usual sense. In fact, one can treat the problem at hand
by making a change in the normalization of both the numerator and the
denominator of equation (1.2.1), eventually
obtaining the same results that we will obtain here in a more direct way
(problem 1.2.2).
. We will verify later on that it is indeed possible to
obtain in this way a useful approximation for some of the observables of
the complete model, despite the divergences that are involved in the
limit, but we should keep in mind that we are dealing with a singular
expansion, so that it should come as no surprise it not everything works
out perfectly as expected. It is in this context that the idea of renormalization appears for the first time with a recognizable meaning.
Unfortunately, this term is used for several different things in the
structure of the theory, but here it really has to do with renormalizing
something in the usual sense. In fact, one can treat the problem at hand
by making a change in the normalization of both the numerator and the
denominator of equation (1.2.1), eventually
obtaining the same results that we will obtain here in a more direct way
(problem 1.2.2).
We will examine here the first-order and second-order terms in
![]() for the expansion of
for the expansion of
![]() , for which we obtain
, for which we obtain
where the first three terms contain (problem 1.2.3)
![\begin{eqnarray*}
f(0) & = & \langle{\cal O}\rangle_{0}, f'(0) & = & -\left[\l...
..._{0}
-\langle{\cal O}\rangle_{0}\langle S_{I}\rangle_{0}\right].
\end{eqnarray*}](img185.gif)
Making ![]() we obtain
we obtain
This is the approximation for
![]() up to the order
up to the order
![]() , that is, effectively up to the order
, that is, effectively up to the order ![]() . We
will use it later on to calculate perturbative approximations for some of
the observables of the model.
. We
will use it later on to calculate perturbative approximations for some of
the observables of the model.
Observe that it is not to be expected that this expansion may produce a
convergent series for the observables of the model. An alternative way to
see this is to observe that there cannot be a non-vanishing convergence
radius for the series of
![]() around
around ![]() in the
complex
in the
complex ![]() plane, because a non-vanishing convergence disk
around zero would include negative values of
plane, because a non-vanishing convergence disk
around zero would include negative values of ![]() , which
correspond to points in the unstable region of the parameter plane of the
model, where we know that it does not exist. At most what we can hope to
obtain are reasonable approximations up to a certain order, which
hopefully will be good enough to allow us to form a correct qualitative
idea about the behavior of the model. Note that the model would be
clearly more useful if it did not cease to exist when we exchange the
sign of the coupling constant. One is led to recall that this is the
expected situation in electrodynamics, in which we can have charges of
either sign.
, which
correspond to points in the unstable region of the parameter plane of the
model, where we know that it does not exist. At most what we can hope to
obtain are reasonable approximations up to a certain order, which
hopefully will be good enough to allow us to form a correct qualitative
idea about the behavior of the model. Note that the model would be
clearly more useful if it did not cease to exist when we exchange the
sign of the coupling constant. One is led to recall that this is the
expected situation in electrodynamics, in which we can have charges of
either sign.
In order to complete the development of our perturbative ideas, we must
now return to the issue of the separation of the action ![]() in parts
in parts
![]() and
and ![]() . This separation will depend on whether we want to
perform calculations in one or the other of the two phases of the model,
the symmetrical phase or the broken-symmetrical phase, whose existence
and nature we discussed in section 1.1. In any case
. This separation will depend on whether we want to
perform calculations in one or the other of the two phases of the model,
the symmetrical phase or the broken-symmetrical phase, whose existence
and nature we discussed in section 1.1. In any case ![]() must
satisfy the two essential conditions: it must be no more than quadratic
on the fields and it must be stable, which means that it must correspond
to a well-behaved theory of free fields, having therefore a lower bound.
must
satisfy the two essential conditions: it must be no more than quadratic
on the fields and it must be stable, which means that it must correspond
to a well-behaved theory of free fields, having therefore a lower bound.
The issue of stability must be examined carefully at this point. As we
saw in section 1.1, in any continuum limit that does not
approach the Gaussian point the parameter ![]() will become strictly
negative. Therefore we cannot include the
will become strictly
negative. Therefore we cannot include the ![]() term in
term in ![]() ,
because this quadratic action would become unbounded from below and the
corresponding measure well be ill-defined even on finite lattices. The
alternative of including only the derivative term in
,
because this quadratic action would become unbounded from below and the
corresponding measure well be ill-defined even on finite lattices. The
alternative of including only the derivative term in ![]() and of
simply including the
and of
simply including the ![]() term in
term in ![]() is also not adequate, since
the free massless theory that results from this has a zero mode that
could be absent from the complete model, leading to the possibility of
the appearance of spurious infrared divergences.
is also not adequate, since
the free massless theory that results from this has a zero mode that
could be absent from the complete model, leading to the possibility of
the appearance of spurious infrared divergences.
In order to avoid possible infrared problems we will introduce into the
model a new parameter
![]() associated to a quadratic term
containing
associated to a quadratic term
containing ![]() , in such a way that the model is not actually
changed. Dealing first with the case in which we are in the symmetrical
phase, we will choose for
, in such a way that the model is not actually
changed. Dealing first with the case in which we are in the symmetrical
phase, we will choose for ![]() the action of the free theory as we
have studied it since the section in [10],
the action of the free theory as we
have studied it since the section in [10],
![\begin{displaymath}
S_{0}[\varphi]=\frac{1}{2}\sum_{\ell}(\Delta_{\ell}\varphi)^{2}
+\frac{\alpha_{0}}{2}\sum_{s}\varphi^{2}(s).
\end{displaymath}](img195.gif)
The interaction part ![]() of the action will contain the remaining
terms of the original action and a term containing
of the action will contain the remaining
terms of the original action and a term containing ![]() with the
opposite sign, so that the sum of
with the
opposite sign, so that the sum of ![]() and
and ![]() continues equal to
the original action. It follows that in this symmetrical phase we will
have for
continues equal to
the original action. It follows that in this symmetrical phase we will
have for ![]()
![\begin{displaymath}
S_{I}=\sum_{s}\left[\frac{\alpha-\alpha_0}{2}\varphi^{2}(s)
+\frac{\lambda}{4}\varphi^{4}(s)\right].
\end{displaymath}](img196.gif)
The parameter ![]() is clearly irrelevant in the exact model and
the final results should be independent of it. We will see later on that
this is indeed the case but, since
is clearly irrelevant in the exact model and
the final results should be independent of it. We will see later on that
this is indeed the case but, since ![]() appears both in
appears both in ![]() and in
and in ![]() , which will be treated in very different ways during the
development of the approximation technique, we will also see that there
are some subtleties relating to the role played by
, which will be treated in very different ways during the
development of the approximation technique, we will also see that there
are some subtleties relating to the role played by ![]() . Up to
this point it seems that we are free to keep the parameter
. Up to
this point it seems that we are free to keep the parameter ![]() finite and non-zero in the
finite and non-zero in the
![]() limit, but it is not very
reasonable to do this because this procedure would correspond to a
diverging mass
limit, but it is not very
reasonable to do this because this procedure would correspond to a
diverging mass ![]() for the distribution defined by
for the distribution defined by ![]() in the
limit. Instead of that, we will choose
in the
limit. Instead of that, we will choose
![]() and
work with an
and
work with an ![]() which is kept finite in the limit, rather than
diverging. What we are hinting at here is that perhaps it is possible to
improve the quality of the approximation by a suitable choice of the free
parameter
which is kept finite in the limit, rather than
diverging. What we are hinting at here is that perhaps it is possible to
improve the quality of the approximation by a suitable choice of the free
parameter ![]() . If we knew beforehand the value
. If we knew beforehand the value ![]() of the
renormalized (physical) mass of the complete model in the limit, we could
even consider making
of the
renormalized (physical) mass of the complete model in the limit, we could
even consider making ![]() . Although it is not apparent at this
moment that we should do this, or that we could do it, since we do not
yet know
. Although it is not apparent at this
moment that we should do this, or that we could do it, since we do not
yet know ![]() , we will see later on that this is, in fact, a natural
and very convenient choice.
, we will see later on that this is, in fact, a natural
and very convenient choice.
In the broken-symmetrical phase we expect that the expectation value of
the field
![]() will be different from zero and, in
order to enable us to develop the perturbative approximation is a simpler
way, it is convenient to first rewrite the model in terms of a shifted
field
will be different from zero and, in
order to enable us to develop the perturbative approximation is a simpler
way, it is convenient to first rewrite the model in terms of a shifted
field ![]() given by
given by
where ![]() is the expectation value of the field which, in the absence
of any external sources breaking the discrete translation invariance of
the lattice, as is our case here, should be constant, having the same
values at all the sites. Since
is the expectation value of the field which, in the absence
of any external sources breaking the discrete translation invariance of
the lattice, as is our case here, should be constant, having the same
values at all the sites. Since ![]() is a constant it follows that the
derivative term of the action remains unchanged. The polynomial terms
which are quadratic and quartic on the fields, however, are transformed
according to the relations
is a constant it follows that the
derivative term of the action remains unchanged. The polynomial terms
which are quadratic and quartic on the fields, however, are transformed
according to the relations
We may neglect the constant terms, that do not depend on the field, since the exponentials of these terms are constant factors that appear both in the numerator and in the denominator of the ratio that defines the observables, thus cancelling off and not affecting in any way the statistical distribution of the model. Doing this we obtain for the complete action of the model
![\begin{displaymath}
S=\sum_{s}\left[\frac{1}{2}\sum_{\mu}(\Delta_{\mu}\varphi')^...
...lambda
v_{R}\varphi'^{3}+\frac{\lambda}{4}\varphi'^{4}\right].
\end{displaymath}](img203.gif)
Since we know that ![]() will always be strictly negative, we
introduce now the parameter
will always be strictly negative, we
introduce now the parameter
![]() and separate the action
into a free part
and separate the action
into a free part
and an interaction part
This is the form of the interaction term to be used in the broken-symmetrical phase of the model. We have therefore a completely well-defined scheme for trying to obtain approximations for the observables of the complete model in the vicinity of the Gaussian point, both in the symmetrical phase and in the broken-symmetrical phase. We must now perform in detail the calculation for some particular observables of the model, always keeping in mind that this is a very singular approximation scheme and that it may turn out that not everything will work as we might hope, in order to verify what we may learn about the structure of the model by means of the use of this technique.
One could imagine that one way to try to get around this problem is to
add to the action a field-independent term
![]() ,
which corresponds to multiplying both the numerator and the denominator
of equation (1.2.1) by a number
,
which corresponds to multiplying both the numerator and the denominator
of equation (1.2.1) by a number
![]() . This corresponds to
a renormalization of the statistical averages that define the
expectation values of the complete model in terms of the expectation
values of the free theory, leading to
. This corresponds to
a renormalization of the statistical averages that define the
expectation values of the complete model in terms of the expectation
values of the free theory, leading to
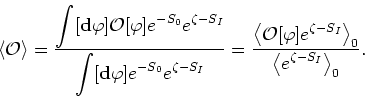
Naturally, this does not change the observables. However, we are now free
to choose ![]() in any way we choose, and we may consider choosing it
so that the quantity
in any way we choose, and we may consider choosing it
so that the quantity ![]() acquires a small or even a vanishing
average value, rather than diverging as
acquires a small or even a vanishing
average value, rather than diverging as ![]() in the limit. It is clear
that in this case
in the limit. It is clear
that in this case ![]() will have to be chosen so as to diverge in the
limit and hence cancel the divergence of the average value of
will have to be chosen so as to diverge in the
limit and hence cancel the divergence of the average value of
![]() . Observe however that in this way we can control only the average value of the difference
. Observe however that in this way we can control only the average value of the difference ![]() , we cannot control the
fluctuations of this quantity, because
, we cannot control the
fluctuations of this quantity, because ![]() cannot depend on the
fields.
cannot depend on the
fields.
If we recall that, as was seen in the text, the large-![]() limit of
equation (1.2.1) is of the type
limit of
equation (1.2.1) is of the type ![]() , it is
reasonable to think that a general criterion or renormalization
condition for the choice of
, it is
reasonable to think that a general criterion or renormalization
condition for the choice of ![]() would be
would be
which causes the limit to cease to be of the type ![]() , but which is a
very complicated condition to implement. To first order, we may think
that the condition
, but which is a
very complicated condition to implement. To first order, we may think
that the condition
![]() should be
sufficient, and it is a condition which is much simpler to deal with.
About this type of renormalization procedure we have the following tasks
to propose:
should be
sufficient, and it is a condition which is much simpler to deal with.
About this type of renormalization procedure we have the following tasks
to propose:
and show that it does not have a finite limit when
![]() .
.