Up: Non-Linear Scalar Models A Previous: Critique of Perturbative Renormalization Contents
TODO: fix all entries; reorganize the references to the first book; include HTML links for the web version.
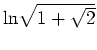 and was obtained from T. L. Hill, ``Statistical Mechanics'', McGraw-Hill,
(1956, reprinted by Dover, 1987), page 329.
and was obtained from T. L. Hill, ``Statistical Mechanics'', McGraw-Hill,
(1956, reprinted by Dover, 1987), page 329.