Next: Bibliography Up: Interactions Between Particles Previous: The Coupling Constant Contents
Using the techniques and ideas developed in section 1.2 we may
try to calculate perturbatively the renormalized coupling constant
![]() , which we wrote in terms of observables of the model in
section 3.1. Using equation (3.1.7) and
calculating the observables involved to first order, with the same choice
, which we wrote in terms of observables of the model in
section 3.1. Using equation (3.1.7) and
calculating the observables involved to first order, with the same choice
![]() that we used for the calculation of the
propagator, we obtain (problem 3.2.1) the
classical result
that we used for the calculation of the
propagator, we obtain (problem 3.2.1) the
classical result
![]() . Naturally, this implies that
. Naturally, this implies that
![]() to first order in
to first order in ![]() , which means to
first order in
, which means to
first order in ![]() , which seems to indicate, in a superficial way,
that we may have a non-vanishing renormalized coupling constant in the
quantum theory. We will see, however, that this is an excessively
superficial analysis and that the real situation is much more complex
than what it indicates.
, which seems to indicate, in a superficial way,
that we may have a non-vanishing renormalized coupling constant in the
quantum theory. We will see, however, that this is an excessively
superficial analysis and that the real situation is much more complex
than what it indicates.
Let us recall that, in the calculation of the propagator, the calculation
of order zero in ![]() resulted in the classical propagator, that
is, in the propagator of the Gaussian ensemble that we are using to
approximate the ensemble of the complete theory, while the calculation to
first order in
resulted in the classical propagator, that
is, in the propagator of the Gaussian ensemble that we are using to
approximate the ensemble of the complete theory, while the calculation to
first order in ![]() gave us quantum corrections to the classical
result. Also, this first-order result was not a small correction of the
zero-order result, but instead was qualitatively different from it. In
the case of the coupling constant it is clear that the zero-order
calculation results in
gave us quantum corrections to the classical
result. Also, this first-order result was not a small correction of the
zero-order result, but instead was qualitatively different from it. In
the case of the coupling constant it is clear that the zero-order
calculation results in ![]() , which is the value of this
quantity in the Gaussian ensemble, while the first-order calculation
gives us the classical result. This situation is to be expected, since we
are now calculating a quantity which is, by definition, at least
proportional to the expansion parameter
, which is the value of this
quantity in the Gaussian ensemble, while the first-order calculation
gives us the classical result. This situation is to be expected, since we
are now calculating a quantity which is, by definition, at least
proportional to the expansion parameter ![]() , and that vanishes when
the expansion parameter vanishes, unlike what was the case for
, and that vanishes when
the expansion parameter vanishes, unlike what was the case for
![]() . Unlike what happened in the case of
. Unlike what happened in the case of ![]() , we are
discussing here a quantity that does not exist at all in the Gaussian
ensemble of the free theory. Just like what happened in the case of the
propagator, it is possible that passing to the next order, which takes us
away from the classical results, will make a qualitative difference.
, we are
discussing here a quantity that does not exist at all in the Gaussian
ensemble of the free theory. Just like what happened in the case of the
propagator, it is possible that passing to the next order, which takes us
away from the classical results, will make a qualitative difference.
These results that we refer to as ``classical'' correspond, in the
traditional language, to Feynman diagrams with zero loops, that is, to
the ``tree'' approximation. These results do not include the effects of
the quantum fluctuations of the fields on the observables. Hence, the
zero-loop approximations do not include the quantum effects contained in
the theory, but only the effects of the classical dynamics of the
fields. In order to include the effect of the quantum fluctuations it is
necessary to do the calculations up to the lowest order of ![]() which includes diagrams with one loop. In the case of
which includes diagrams with one loop. In the case of ![]() this meant
doing calculations up to the first order in
this meant
doing calculations up to the first order in ![]() , but in order
to explore the effects of the quantum fluctuations of the fields on the
renormalized coupling constant it is necessary to calculate
, but in order
to explore the effects of the quantum fluctuations of the fields on the
renormalized coupling constant it is necessary to calculate ![]() to second order in
to second order in ![]() , thus including diagrams with up to one
loop. These calculations to order
, thus including diagrams with up to one
loop. These calculations to order
![]() are considerably
longer and more complex than those to the first order, and involve
quantities with strong divergences that behave as either
are considerably
longer and more complex than those to the first order, and involve
quantities with strong divergences that behave as either ![]() or as
or as
![]() , all of which cancel out completely from the final results.
Doing the calculation in the symmetrical phase, with vanishing momenta on
the four external legs, we obtain
(problem 3.2.2)
, all of which cancel out completely from the final results.
Doing the calculation in the symmetrical phase, with vanishing momenta on
the four external legs, we obtain
(problem 3.2.2)
![\begin{displaymath}
\lambda_{R}=\frac{\displaystyle \lambda\left[
1-4\frac{\alph...
... \left[1-\frac{\alpha_{R}-\alpha_{0}}{\alpha_{0}}\right]^{4}},
\end{displaymath}](img645.gif)
where the dimensionless sum
![]() that appears here is
given, in terms of the dimensionless free propagator
that appears here is
given, in terms of the dimensionless free propagator
![]() , by
, by
In principle it is also possible to do the calculation in the
broken-symmetrical phase
(problem 3.2.3), but currently we do
not yet know the answer for that case. Making the choice
![]() as before, we obtain
as before, we obtain
Observe that, since the sum is a positive quantity, the correction is
always negative, tending to decrease the magnitude of the positive
classical result. We may try to evaluate the behavior of the sum ![]() for large values of
for large values of ![]() by means of approximations by integrals, as we
did before in other cases. Doing this
(problem 3.2.4) we obtain the following results, for
the usual values of the dimension
by means of approximations by integrals, as we
did before in other cases. Doing this
(problem 3.2.4) we obtain the following results, for
the usual values of the dimension ![]() :
:
where ![]() is the total solid angle of
is the total solid angle of ![]() -dimensional space. We
see therefore that the second-order result is divergent for
-dimensional space. We
see therefore that the second-order result is divergent for ![]() and
and
![]() , and finite for
, and finite for ![]() . Observe that, in order for the results
in
. Observe that, in order for the results
in ![]() and
and ![]() to make any sense, it is necessary that we make
to make any sense, it is necessary that we make
![]() in the continuum limit, thus forcing us to return
to the Gaussian point. In
in the continuum limit, thus forcing us to return
to the Gaussian point. In ![]() this takes us back to the free theory
but, curiously, despite this limitation the result is still of some
interest in the case
this takes us back to the free theory
but, curiously, despite this limitation the result is still of some
interest in the case ![]() , because in this case the dimensionfull
coupling constant is given by
, because in this case the dimensionfull
coupling constant is given by
![]() and we therefore have, in terms of the dimensionfull quantities, a finite
expression,
and we therefore have, in terms of the dimensionfull quantities, a finite
expression,
where the dimensionfull quantity
![]() has a finite limit, so
long as we have a finite and non-vanishing renormalized mass
has a finite limit, so
long as we have a finite and non-vanishing renormalized mass ![]() ,
,
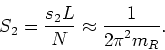
This seems to indicate that in ![]() there are non-trivial limits, with
there are non-trivial limits, with
![]() , that approach the Gaussian point, where both
, that approach the Gaussian point, where both
![]() and
and ![]() are zero. We can use this
are zero. We can use this ![]() result to
exhibit explicitly renormalization flows
result to
exhibit explicitly renormalization flows
![]() , in the
parameter space of the corresponding model, that approach the Gaussian
point in such a way that both
, in the
parameter space of the corresponding model, that approach the Gaussian
point in such a way that both ![]() and
and ![]() are different
from zero in the limit (problem 3.2.5).
are different
from zero in the limit (problem 3.2.5).
Of course this type of limit constitutes a small subset of all possible
alternatives, in which we approach, in the limit, some other arbitrary
point of the critical curve, rather than the Gaussian point. About these
other possibilities our perturbative approximation has nothing to say,
but note that, is we assume that there is at least one such limit for
each one of these points, in which ![]() is finite, it follows
immediately that it is necessary that
is finite, it follows
immediately that it is necessary that
![]() over the
whole critical curve, when we make
over the
whole critical curve, when we make
![]() . This means that
it is highly likely that the ensemble of the renormalized theory becomes
Gaussian over the critical curve in the continuum limit. Since
. This means that
it is highly likely that the ensemble of the renormalized theory becomes
Gaussian over the critical curve in the continuum limit. Since
![]() is a dimensionless quantity that measures, just like
is a dimensionless quantity that measures, just like
![]() , a moment of the distribution of the renormalized model, it
is very reasonable to think that both should have the same particular
type of behavior in the locus of the parameter plane of the model where
the critical transition takes place. In other words, it is reasonable to
think that
, a moment of the distribution of the renormalized model, it
is very reasonable to think that both should have the same particular
type of behavior in the locus of the parameter plane of the model where
the critical transition takes place. In other words, it is reasonable to
think that ![]() should always go to zero over the critical curve
in the continuum limit, as part of the critical behavior of the model.
should always go to zero over the critical curve
in the continuum limit, as part of the critical behavior of the model.
We may also try to extract some information of the result in
equation (3.2.2) in the case ![]() . In this case
our result seems to indicate that we will have a finite and non-vanishing
. In this case
our result seems to indicate that we will have a finite and non-vanishing
![]() as a function of
as a function of ![]() and
and ![]() , since the sum
, since the sum
![]() is finite and non-vanishing. It is very reasonable to think that
the dimensionless quantities like
is finite and non-vanishing. It is very reasonable to think that
the dimensionless quantities like ![]() will always be finite in
the limit, when we make
will always be finite in
the limit, when we make
![]() , since they do not scale
with
, since they do not scale
with ![]() . Since we have that
. Since we have that
![]() , for
dimensions
, for
dimensions ![]() we have that a finite
we have that a finite ![]() implies a
vanishing
implies a
vanishing ![]() in the limit. We establish in this way the
expectation that the model is completely trivial in
in the limit. We establish in this way the
expectation that the model is completely trivial in ![]() , with
, with
![]() finite and
finite and ![]() vanishing over the critical curve.
Of course this conclusion depends on the higher-order terms of the
perturbative series of
vanishing over the critical curve.
Of course this conclusion depends on the higher-order terms of the
perturbative series of ![]() being all finite, besides the series
being convergent. Obviously, none of these two things is guaranteed. One
might even imagine that the series could end up converging to zero, a
hypothesis which would not change the physical meaning of the theory,
since that meaning is defined in terms of
being all finite, besides the series
being convergent. Obviously, none of these two things is guaranteed. One
might even imagine that the series could end up converging to zero, a
hypothesis which would not change the physical meaning of the theory,
since that meaning is defined in terms of ![]() , which would
still vanish in the limit. However, that hypothesis would make sense in
terms of the critical behavior of the dimensionless quantity
, which would
still vanish in the limit. However, that hypothesis would make sense in
terms of the critical behavior of the dimensionless quantity
![]() , as we discussed above in the case
, as we discussed above in the case ![]() .
.
In the case ![]() we cannot conclude anything about the behavior of the
theory from our results, since in this case
we cannot conclude anything about the behavior of the
theory from our results, since in this case ![]() diverges
logarithmically while
diverges
logarithmically while
![]() . We can confirm our
analytical estimates of the dependencies of
. We can confirm our
analytical estimates of the dependencies of ![]() on
on ![]() and calculate
approximately the relevant coefficients, performing numerically the sum
on finite lattices (problem 3.2.6). The results
obtained in this way, for
and calculate
approximately the relevant coefficients, performing numerically the sum
on finite lattices (problem 3.2.6). The results
obtained in this way, for ![]() , are shown in the graphs found in
figures from 3.2.1 to 3.2.5.
Simple but good-quality curve fittings, with only a single parameter in
the cases
, are shown in the graphs found in
figures from 3.2.1 to 3.2.5.
Simple but good-quality curve fittings, with only a single parameter in
the cases ![]() ,
, ![]() and
and ![]() , and with three parameters in the cases
, and with three parameters in the cases
![]() and
and ![]() , give the approximate results
, give the approximate results
One may also consider calculating the expectation value of the field and
of the propagator up to order
![]() , which corresponds to the
inclusion of diagrams with up to two loops. In some cases one may still
be able to extract from these calculations some useful information such
as, for example, for the determination of the critical curve
(problem 3.2.7) and, in some cases, for the
determination of the renormalized mass
(problem 3.2.8). However, in general the results
of these calculations include divergent sums and it is not possible to
use them in a systematic way to establish a system of successive
approximations, which hopefully would be increasingly precise, for all
the observables of the theory.
, which corresponds to the
inclusion of diagrams with up to two loops. In some cases one may still
be able to extract from these calculations some useful information such
as, for example, for the determination of the critical curve
(problem 3.2.7) and, in some cases, for the
determination of the renormalized mass
(problem 3.2.8). However, in general the results
of these calculations include divergent sums and it is not possible to
use them in a systematic way to establish a system of successive
approximations, which hopefully would be increasingly precise, for all
the observables of the theory.
Therefore, we see that we do not really have a complete expansion for the
![]() model, but only a set of approximations that work
reasonably well in some cases. What we have here is not a consistent and
systematic series development, but only a set of isolated approximations
whose validity can only be verified, ultimately, by direct comparison
with numerical results or other non-perturbative approximations. Observe
that this behavior of the perturbative expansion is due to the exchange
of the order of the two limits involved, the continuum limit and the
series summation limit. For finite
model, but only a set of approximations that work
reasonably well in some cases. What we have here is not a consistent and
systematic series development, but only a set of isolated approximations
whose validity can only be verified, ultimately, by direct comparison
with numerical results or other non-perturbative approximations. Observe
that this behavior of the perturbative expansion is due to the exchange
of the order of the two limits involved, the continuum limit and the
series summation limit. For finite ![]() all the terms of the expansion are
finite and the series may be convergent, or at least asymptotic, but in
the
all the terms of the expansion are
finite and the series may be convergent, or at least asymptotic, but in
the
![]() limit the individual terms become infinite and
nothing can be done to salvage the situation in general, except making
the parameters of the model converge sufficiently fast to the Gaussian
point. In order to make use of the series it is imperative to first sum
it on finite lattices and only then take the continuum limit, one cannot
invert the order of the limits.
limit the individual terms become infinite and
nothing can be done to salvage the situation in general, except making
the parameters of the model converge sufficiently fast to the Gaussian
point. In order to make use of the series it is imperative to first sum
it on finite lattices and only then take the continuum limit, one cannot
invert the order of the limits.
In conclusion, we verify that in the case of the coupling constant we do
not have a perturbative approximation as successful as in the cases of
the renormalized mass and of the expectation value of the field. It
allows us to go so far as to formulate the conjecture that, in any
dimension ![]() , in any limit where
, in any limit where
![]() ,
,
![]() and
and
![]() , where
, where
![]() is a point over the critical curve, we
have
is a point over the critical curve, we
have
![]() . However, it does not allow us to make
concrete predictions about the behavior of the model away from the
Gaussian point, as we were able to do for the renormalized mass and the
expectation value of the field. It seems, therefore, that the discussion
of the perturbative approximation should be separated in two parts, the
first one being relative to the calculation of the quantities involving,
at most, the second moment of the distribution of the model, as is the
case for
. However, it does not allow us to make
concrete predictions about the behavior of the model away from the
Gaussian point, as we were able to do for the renormalized mass and the
expectation value of the field. It seems, therefore, that the discussion
of the perturbative approximation should be separated in two parts, the
first one being relative to the calculation of the quantities involving,
at most, the second moment of the distribution of the model, as is the
case for ![]() and
and ![]() , while the second one relates to the
quantities involving the higher-order moments, such as
, while the second one relates to the
quantities involving the higher-order moments, such as ![]() .
.
We see that the reason why the approximation does not work so well for
the coupling constant is the fact that it is not possible to impose, in
this case, the equivalent of the condition
![]() used
in the case of the renormalized mass, which transformed the first-order
perturbative approximation into a self-consistent Gaussian
approximation. This is due, of course, to the fact that the Gaussian
model, the only one we know how to solve exactly, has no moments of order
greater than two, whose coefficients may be adjusted so as to reproduce
faithfully the characteristics of the ensemble of the complete model.
When we choose
used
in the case of the renormalized mass, which transformed the first-order
perturbative approximation into a self-consistent Gaussian
approximation. This is due, of course, to the fact that the Gaussian
model, the only one we know how to solve exactly, has no moments of order
greater than two, whose coefficients may be adjusted so as to reproduce
faithfully the characteristics of the ensemble of the complete model.
When we choose
![]() we are making the moment of order
two of the Gaussian ensemble reproduce in a perfect way the corresponding
moment of the ensemble of the complete model, so that the difference
between the two distributions can in fact be considered a small
perturbation of the Gaussian distribution, in so far as that observable
is concerned. However, independently of any choices of parameters, the
fourth-order moment of the Gaussian ensemble is always zero and cannot be
adjusted to reproduce the corresponding moment of the complete ensemble.
Therefore, the fourth-order moment can never be understood as a small
perturbation when we are dealing with observables that only exist when
this moment is not zero.
we are making the moment of order
two of the Gaussian ensemble reproduce in a perfect way the corresponding
moment of the ensemble of the complete model, so that the difference
between the two distributions can in fact be considered a small
perturbation of the Gaussian distribution, in so far as that observable
is concerned. However, independently of any choices of parameters, the
fourth-order moment of the Gaussian ensemble is always zero and cannot be
adjusted to reproduce the corresponding moment of the complete ensemble.
Therefore, the fourth-order moment can never be understood as a small
perturbation when we are dealing with observables that only exist when
this moment is not zero.
It is important that we discuss here the role of the traditional scheme
of perturbative renormalization, in the context of the calculations on
the lattice3.1. First of all,
there can be no doubt that the definition of the model on the lattice
implies the existence of well-defined relations
![]() and
and
![]() between
these renormalized quantities and the parameters of the model, for any
values of these parameters within the stable region of the parameter
plane of the models and in any dimension
between
these renormalized quantities and the parameters of the model, for any
values of these parameters within the stable region of the parameter
plane of the models and in any dimension ![]() , for finite lattices, and
over the critical curve in any dimension
, for finite lattices, and
over the critical curve in any dimension ![]() , in the continuum
limit. Analogously, for any observable
, in the continuum
limit. Analogously, for any observable ![]() that is physically relevant
we have a well-defined relation
that is physically relevant
we have a well-defined relation
![]() , under the same
conditions. What we discover when we work out the development of
perturbation theory is that the perturbative approximations for the
relations between the observables
, under the same
conditions. What we discover when we work out the development of
perturbation theory is that the perturbative approximations for the
relations between the observables ![]() ,
, ![]() and
and ![]() and the parameters
and the parameters ![]() and
and ![]() are singular, in the sense that
they contain quantities that diverge in the continuum limit.
are singular, in the sense that
they contain quantities that diverge in the continuum limit.
The traditional perturbative renormalization scheme consists of giving
up, at this point, any effort of extracting from the theory the relations
![]() ,
,
![]() and
and
![]() that it contains. In addition to this, on each
finite lattice, where all quantities are finite, we may consider
rewriting
that it contains. In addition to this, on each
finite lattice, where all quantities are finite, we may consider
rewriting ![]() directly in terms of
directly in terms of ![]() and
and ![]() ,
eliminating the parameters
,
eliminating the parameters ![]() and
and ![]() from the picture in
favor of their renormalized counterparts, and thus obtaining a relation
from the picture in
favor of their renormalized counterparts, and thus obtaining a relation
![]() that, possibly, will not contain any
quantities that diverge in the continuum limit. If it is possible to do
this, then the relation obtained is a well-behaved perturbative
approximation of
that, possibly, will not contain any
quantities that diverge in the continuum limit. If it is possible to do
this, then the relation obtained is a well-behaved perturbative
approximation of ![]() in terms of
in terms of ![]() and
and ![]() , and we
may then take the continuum limit without stumbling on any singularities.
If it is possible to do this for the perturbative calculations to all
orders, then we say that the theory is perturbatively renormalizable, and
the scheme produces a complete perturbative series in the continuum
limit, with finite individual terms, which may or may not be convergent.
Since
, and we
may then take the continuum limit without stumbling on any singularities.
If it is possible to do this for the perturbative calculations to all
orders, then we say that the theory is perturbatively renormalizable, and
the scheme produces a complete perturbative series in the continuum
limit, with finite individual terms, which may or may not be convergent.
Since ![]() and
and ![]() are not directly observable, while
are not directly observable, while
![]() and
and ![]() presumably are, the resulting function
presumably are, the resulting function
![]() is a direct relation between observables of
the theory, so that not much seems to be lost when one does this.
is a direct relation between observables of
the theory, so that not much seems to be lost when one does this.
Of course, rewriting ![]() in terms of
in terms of ![]() and
and ![]() on
finite lattices may not be easy, in fact, it may not be possible at all
in closed form, so one may be compelled to re-expand the expressions that
appear when one tries to do this, possibly neglecting higher-order terms
in order to keep consistent powers of the expansion parameters. All this
considerably complicates the whole argument and makes it more difficult
to understand what is really going on when one does all this. Let us try
to exemplify this in the context of the calculations that we made here,
at first in a very simple and possibly incomplete way. We have calculated
one-loop approximations for
on
finite lattices may not be easy, in fact, it may not be possible at all
in closed form, so one may be compelled to re-expand the expressions that
appear when one tries to do this, possibly neglecting higher-order terms
in order to keep consistent powers of the expansion parameters. All this
considerably complicates the whole argument and makes it more difficult
to understand what is really going on when one does all this. Let us try
to exemplify this in the context of the calculations that we made here,
at first in a very simple and possibly incomplete way. We have calculated
one-loop approximations for ![]() and
and ![]() , obtaining
expressions of the form
, obtaining
expressions of the form
We saw that, while the one-loop propagator is entirely finite, the renormalized mas parameter being given by
the one-loop coupling constant contains the divergent sum ![]() , being
given by
, being
given by
We proceed then to a change of variables, introducing a new parameter
![]() in place of
in place of ![]() , defined by the relation
, defined by the relation
Note that this mixes powers of ![]() and corresponds, therefore, to a
reorganization of the perturbative expansion. Substituting this
expression for
and corresponds, therefore, to a
reorganization of the perturbative expansion. Substituting this
expression for ![]() in the result for
in the result for ![]() we verify that
the divergent terms of order
we verify that
the divergent terms of order
![]() cancel out, so that we
obtain
cancel out, so that we
obtain
We now argue that we can neglect in this equation the terms of orders
![]() and
and
![]() , not because they are small,
since they are clearly divergent in the limit, but under the allegation
that they will cancel out with the remaining higher-order terms that have
not yet been explicitly included in this analysis. This is the first
condition involved in the criterion of perturbative renormalizability in
a weak sense, term by term in the perturbative expansion, without
preoccupation with its convergence. What we are requiring here is that
the divergent terms cancel out, not in the original series, but after its
reorganization by the change of variables from
, not because they are small,
since they are clearly divergent in the limit, but under the allegation
that they will cancel out with the remaining higher-order terms that have
not yet been explicitly included in this analysis. This is the first
condition involved in the criterion of perturbative renormalizability in
a weak sense, term by term in the perturbative expansion, without
preoccupation with its convergence. What we are requiring here is that
the divergent terms cancel out, not in the original series, but after its
reorganization by the change of variables from ![]() to
to
![]() . Under these conditions we have
. Under these conditions we have
which shows that our change of variables is in fact a change from an
expansion in terms of the basic parameter ![]() to another expansion
in terms of the renormalized parameter
to another expansion
in terms of the renormalized parameter ![]() . If we now write
. If we now write
![]() in terms of
in terms of ![]() ,
,
we see that ![]() should diverge in order for this relation to be
valid. This is the opposite of what we saw in the original perturbative
expansion, where we verified that
should diverge in order for this relation to be
valid. This is the opposite of what we saw in the original perturbative
expansion, where we verified that ![]() must go to zero in order for
the perturbative approximation to be valid. However, since by now we have
given up obtaining from the theory the relations between the basic
quantities and the renormalized quantities, we might as well just not
worry about this any more, and simply disregard the equation above. Of
course, one cannot avoid the strong impression that this whole procedure
is mired with guesswork and arbitrariness. It certainly looks like it
would be very difficult to show that all the facts assumed do indeed hold
to all orders and hence to establish the results of this procedure on a
firm logical basis.
must go to zero in order for
the perturbative approximation to be valid. However, since by now we have
given up obtaining from the theory the relations between the basic
quantities and the renormalized quantities, we might as well just not
worry about this any more, and simply disregard the equation above. Of
course, one cannot avoid the strong impression that this whole procedure
is mired with guesswork and arbitrariness. It certainly looks like it
would be very difficult to show that all the facts assumed do indeed hold
to all orders and hence to establish the results of this procedure on a
firm logical basis.
Anyway, up to this point the change of variables has not really been of
any use, since it simply introduced another parameter ![]() that
ended up being another name for
that
ended up being another name for ![]() . No additional information
about the relation between
. No additional information
about the relation between ![]() and the basic parameters of the
model was obtained. It is important to emphasize that this fact is no
more than a limitation of the perturbative method and that this relation
undoubtedly exists in the model defined by means of the lattice. In order
to show the possible usefulness of the perturbative renormalization
scheme, we may now consider the calculation of a third observable
and the basic parameters of the
model was obtained. It is important to emphasize that this fact is no
more than a limitation of the perturbative method and that this relation
undoubtedly exists in the model defined by means of the lattice. In order
to show the possible usefulness of the perturbative renormalization
scheme, we may now consider the calculation of a third observable ![]() ,
at first in terms of
,
at first in terms of ![]() and
and ![]() , resulting in a relation of
the type
, resulting in a relation of
the type
which presumably contains some terms with divergent factors. We may now
substitute ![]() for
for ![]() , re-expanding the resulting
expression and neglecting once more the higher-order terms that appear.
With some more manipulation we may also substitute
, re-expanding the resulting
expression and neglecting once more the higher-order terms that appear.
With some more manipulation we may also substitute ![]() for
for
![]() , thus obtaining a new relation
, thus obtaining a new relation
which, so long as the model is perturbatively renormalizable, should not
contain any divergences. In this way we extract from the model a
well-behaved relation between ![]() ,
, ![]() and
and ![]() ,
although the fundamental perturbative expansion in terms of
,
although the fundamental perturbative expansion in terms of ![]() and
and
![]() is not well behaved. As an example of such an observable, we
may consider the coupling constant for a non-vanishing momentum
is not well behaved. As an example of such an observable, we
may consider the coupling constant for a non-vanishing momentum
![]() , a quantity which is related in a direct way to the scattering
cross-sections. Calculating the coupling constant for the same momentum
, a quantity which is related in a direct way to the scattering
cross-sections. Calculating the coupling constant for the same momentum
![]() on all the four external legs, up to order
on all the four external legs, up to order ![]() , we
obtain (problem 3.2.9)
, we
obtain (problem 3.2.9)
where the sum
![]() is given by
is given by
![\begin{displaymath}
s_{2}(\vec{k},\alpha_{0})=\frac{1}{N^d}\sum_{\vec{\vec{k}_{1...
...c{k})+\alpha_{0}]
[\rho^{2}(\vec{k}_{1}-\vec{k})+\alpha_{0}]}.
\end{displaymath}](img687.gif)
Proceeding with the substitution of ![]() by
by
![]() we obtain
we obtain
The difference of the two sums can be evaluated for small values of the
momentum ![]() with the help of approximations by integrals and,
doing this in
with the help of approximations by integrals and,
doing this in ![]() and for large values of
and for large values of ![]() (problem 3.2.10), we obtain a finite result,
(problem 3.2.10), we obtain a finite result,
![\begin{displaymath}
\lambda_{R}(\vec{k})=\lambda_{R}\left[1+
24\pi^{2}\lambda_{R}\frac{k^{2}}{L^{6}m_{R}^{6}}\right].
\end{displaymath}](img690.gif)
We say that the theory is perturbatively renormalizable if it is possible
to do this in each order of perturbation theory, and hence to obtain
predictions with arbitrarily high precision for ![]() , given values of
, given values of
![]() and
and ![]() . Note that, if we imagine that the theory
is in fact trivial, then we see that this result is not wrong, but that
is is simply rather irrelevant, because in this case the only possible
value for
. Note that, if we imagine that the theory
is in fact trivial, then we see that this result is not wrong, but that
is is simply rather irrelevant, because in this case the only possible
value for ![]() is zero and the relation simply shows that
is zero and the relation simply shows that
![]() for any
for any ![]() . We can see now that there is
in fact a rather subtle problem behind all this. When we do this kind of
manipulation we are giving up obtaining from the theory the relations
between
. We can see now that there is
in fact a rather subtle problem behind all this. When we do this kind of
manipulation we are giving up obtaining from the theory the relations
between
![]() and
and
![]() and, instead of
that, we implicitly assume that certain values of
and, instead of
that, we implicitly assume that certain values of ![]() and
and
![]() are possible in the context of the model defined in a
non-perturbative way by means of the lattice. This seems to be a very
reasonable thing to do in a model which is defined with two free
parameters, and we certainly know which values are or are not possible
for
are possible in the context of the model defined in a
non-perturbative way by means of the lattice. This seems to be a very
reasonable thing to do in a model which is defined with two free
parameters, and we certainly know which values are or are not possible
for ![]() and
and ![]() . However, we do not have now any information
about which values are in fact possible for the renormalized
parameter
. However, we do not have now any information
about which values are in fact possible for the renormalized
parameter ![]() , according to the non-perturbative definition of
the model. Therefore, we do now know which values we may in fact use for
, according to the non-perturbative definition of
the model. Therefore, we do now know which values we may in fact use for
![]() in this perturbative renormalization scheme.
in this perturbative renormalization scheme.
It is implicitly assumed, in the traditional perturbative renormalization
scheme, that the possible values for
![]() are the
same which are possible for
are the
same which are possible for
![]() . However, in general it is
possible that this is not true, and that there are restrictions for the
images of the relations
. However, in general it is
possible that this is not true, and that there are restrictions for the
images of the relations
![]() and
and
![]() determined by the non-perturbative
definition of the models. One restriction that we already know to exist
in this model is that
determined by the non-perturbative
definition of the models. One restriction that we already know to exist
in this model is that
![]() , while the parameter
, while the parameter ![]() can be either positive or negative on finite lattices, and must become
negative in the continuum limit, as we saw in section 1.3.
Another fact, which is even more important than this one, is that there
certainly are important restrictions for
can be either positive or negative on finite lattices, and must become
negative in the continuum limit, as we saw in section 1.3.
Another fact, which is even more important than this one, is that there
certainly are important restrictions for ![]() in a model that
ends up being trivial, in which the only possible value for
in a model that
ends up being trivial, in which the only possible value for ![]() in the
in the
![]() limit is zero. We can always determine
beforehand which values are possible for
limit is zero. We can always determine
beforehand which values are possible for
![]() , but we
cannot do the same for
, but we
cannot do the same for
![]() . Triviality implies
that the usual implicit hypothesis, that the possible values for
. Triviality implies
that the usual implicit hypothesis, that the possible values for
![]() are the same which are possible for
are the same which are possible for
![]() , is false. To continue with the usual perturbative
renormalization scheme under these conditions can only produce fictitious
results, without any physical or mathematical relevance.
, is false. To continue with the usual perturbative
renormalization scheme under these conditions can only produce fictitious
results, without any physical or mathematical relevance.
The conclusion is that a model satisfying the criterion of perturbative renormalizability is not sufficient to guarantee the usefulness of its perturbative expansion, renormalized in the usual way. It is also necessary to determine the values which are actually possible for the renormalized parameters, in terms of which one chooses to write the renormalized perturbative expansion. In regard to this aspect of the structure of the theory it is important to emphasize the profound difference between a truly physical theory, such as quantum electrodynamics, and models that have only the role of mathematical laboratories, such as the polynomial models. In quantum electrodynamics we can go to the laboratory and determine experimentally the values of the renormalized mass and of the renormalized coupling constant, that is, of the mass and charge of the electron, thus establishing that certain values are possible for these quantities. On the other hand, in the laboratory models we are limited to what we can calculate analytically or numerically and we must extract this type of information from the relations that the models establish between the renormalized quantities and the parameters involved in their definitions. Since perturbation theory is not able to give us these relations in a complete form, it only remains for us to try non-perturbative methods, such as computational stochastic simulations, as tools to establish the possible values for the renormalized parameters. Another way to characterize this profound difference is to say that, in the case of a truly physical theory, we have access to the use of the ultimate computer: the fundamental laws of physics at play in nature.
Note: Some of the calculations contained in some of these problems are really very long, and a considerable amount of organization and care is needed to get to the end without errors. The problems containing such long calculations are marked with three stars.
![\begin{displaymath}
\lambda_{R}=\frac{\displaystyle \lambda\left[
1-4\frac{\alph...
... \left[1-\frac{\alpha_{R}-\alpha_{0}}{\alpha_{0}}\right]^{4}}.
\end{displaymath}](img694.gif)
Note that, since ![]() itself is already a first-order quantity
in
itself is already a first-order quantity
in ![]() , in order to keep consistent orders of the expansion
parameter the numerator of equation (3.1.7)
should be calculated to second order, while it is enough to calculate the
denominator to first order.
, in order to keep consistent orders of the expansion
parameter the numerator of equation (3.1.7)
should be calculated to second order, while it is enough to calculate the
denominator to first order.
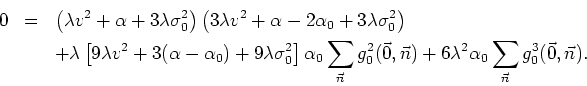
Next evaluate the asymptotic behavior of the new sum that appears,
![\begin{displaymath}
s_{3}(\alpha_{0})=\sum_{\vec{v}}g_{0}^{3}(\vec{0},\vec{n})
=...
...)+\alpha_{0}]
[\rho^{2}(\vec{k}_{1}+\vec{k}_{2})+\alpha_{0}]}.
\end{displaymath}](img699.gif)
Finally, recalling that ![]() must go to zero as
must go to zero as ![]() in the
limit, make
in the
limit, make ![]() and show that, in the continuum limit, one recovers
the one-loop result for the equation of the critical curve,
and show that, in the continuum limit, one recovers
the one-loop result for the equation of the critical curve,
Therefore, we conclude that the equation of the critical curve does not
contain corrections of order ![]() and that any correction to the
order-
and that any correction to the
order-![]() result must be at least of order
result must be at least of order ![]() .
.
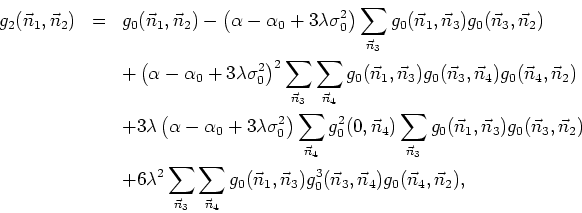
which, in momentum space, can be written as
![\begin{eqnarray*}
N^{d}\widetilde g_{2}(\vec{k}) & = & \frac{1}{\rho^{2}(\vec{k}...
...}{[\rho^{2}(\vec{k})+\alpha_{0}]^{2}}
s_{3}(\vec{k},\alpha_{0}),
\end{eqnarray*}](img704.gif)
where the sum ![]() is given by
is given by
![\begin{displaymath}
s_{3}(\vec{k},\alpha_{0})=\frac{1}{N^{2d}}\sum_{\vec{k}_{1},...
..._{0}]
[\rho^{2}(\vec{k}-\vec{k}_{1}-\vec{k}_{2})+\alpha_{0}]}.
\end{displaymath}](img706.gif)
Observe that, since ![]() must still vanish over the critical
curve, and the equation of that curve did not change up to the order
must still vanish over the critical
curve, and the equation of that curve did not change up to the order
![]() , as we saw in problem 3.2.7,
we should expect that the renormalized mass also does not change up to
this order. Discover whether or not it is possible to choose
, as we saw in problem 3.2.7,
we should expect that the renormalized mass also does not change up to
this order. Discover whether or not it is possible to choose ![]() in an appropriate way and thus show that the renormalized mass also does
not change up to this order, establishing therefore the consistency of
the two calculations3.3.
in an appropriate way and thus show that the renormalized mass also does
not change up to this order, establishing therefore the consistency of
the two calculations3.3.
where the sum ![]() is given by
is given by
![\begin{displaymath}
s_{2}(\vec{k},\alpha_{0})=\frac{1}{N^d}\sum_{\vec{\vec{k}_{1...
...c{k})+\alpha_{0}]
[\rho^{2}(\vec{k}_{1}-\vec{k})+\alpha_{0}]}.
\end{displaymath}](img687.gif)
Note that, since
![]() itself is already a first-order
quantity in
itself is already a first-order
quantity in ![]() , in order to keep consistent orders of the
expansion parameter the numerator of the equation that defines
, in order to keep consistent orders of the
expansion parameter the numerator of the equation that defines
![]() should be calculated to second order, while it is
enough to calculate the denominator to first order.
should be calculated to second order, while it is
enough to calculate the denominator to first order.