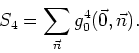Next: The Sigma-Model Limit Up: The Polynomial Model Previous: Perturbation Theory Contents
Having developed in section 1.2 the ideas about the perturbative
approximation for the observables of the
![]() model, we
will now discuss the calculation of some of the observables of the model
to first order in
model, we
will now discuss the calculation of some of the observables of the model
to first order in ![]() which, in the cases to be examined here,
is also known as the ``one-loop'' order1.2. The first thing that we will try to calculate will be the
position of the critical curve near the Gaussian point. In order to to
this we will examine the expectation value of the field,
which, in the cases to be examined here,
is also known as the ``one-loop'' order1.2. The first thing that we will try to calculate will be the
position of the critical curve near the Gaussian point. In order to to
this we will examine the expectation value of the field,
which functions as an order parameter for the phase transition that
exists in the model. Of course, if we have in the model a non-vanishing
external source ![]() , then we should expect that
, then we should expect that ![]() is also
non-vanishing. The situation of spontaneous symmetry breaking is that in
which we have
is also
non-vanishing. The situation of spontaneous symmetry breaking is that in
which we have ![]() even when
even when ![]() . Therefore, we will consider
here the case
. Therefore, we will consider
here the case ![]() and try to verify whether or not it is possible to
obtain solutions of the model with
and try to verify whether or not it is possible to
obtain solutions of the model with ![]() in the limit in which
in the limit in which
![]() . Observe that only in this limit of large lattices
one can expect to obtain a situation of phase transition, with the
existence of two distinct phases in the parameter plane of the model,
separated by a phase-transition curve.
. Observe that only in this limit of large lattices
one can expect to obtain a situation of phase transition, with the
existence of two distinct phases in the parameter plane of the model,
separated by a phase-transition curve.
In the symmetrical phase we necessarily have that ![]() , while in the
broken-symmetrical phase we may have
, while in the
broken-symmetrical phase we may have ![]() . If the phase
transition is of second order with respect to this parameter, as it is to
be expected, then the critical curve is the geometrical locus in the
parameter plane
. If the phase
transition is of second order with respect to this parameter, as it is to
be expected, then the critical curve is the geometrical locus in the
parameter plane
![]() of the model where the solution
of the model where the solution
![]() becomes the only possibility, when we move from the
broken-symmetrical phase to the symmetrical phase in the parameter
plane. What we will do is to determine the values of
becomes the only possibility, when we move from the
broken-symmetrical phase to the symmetrical phase in the parameter
plane. What we will do is to determine the values of
![]() for which
for which ![]() is a possibility and then impose that
is a possibility and then impose that ![]() be the only solution, so as to determine the critical curve. Along the
process, a trivial
be the only solution, so as to determine the critical curve. Along the
process, a trivial ![]() solution that exists in all the parameter
plane will be factored out and eliminated. In the broken-symmetrical
phase this solution corresponds, to make an analogy with the classical
case, to the unstable solution in which the system is at the local
maximum of the potential at
solution that exists in all the parameter
plane will be factored out and eliminated. In the broken-symmetrical
phase this solution corresponds, to make an analogy with the classical
case, to the unstable solution in which the system is at the local
maximum of the potential at ![]() .
.
In order to perform this calculation we must use the separation of the
action in the free and interaction parts given in
equations (1.2.4) and (1.2.5),
which are those that should be used in the broken-symmetrical phase.
First of all we write the definition of ![]() , that is, that it is the
expectation value of the original field
, that is, that it is the
expectation value of the original field
![]() . Next we
use the perturbative expansion given in
equation (1.2.3) in order to write the expectation
values involved, limiting ourselves to the terms of order zero and
one. We choose arbitrarily the site of the lattice with integer
coordinates
. Next we
use the perturbative expansion given in
equation (1.2.3) in order to write the expectation
values involved, limiting ourselves to the terms of order zero and
one. We choose arbitrarily the site of the lattice with integer
coordinates
![]() in order to do the calculation, a choice
which is possible due to the discrete translation invariance of the
lattice. Doing all this we obtain
in order to do the calculation, a choice
which is possible due to the discrete translation invariance of the
lattice. Doing all this we obtain
Since
![]() by construction, several terms
vanish and we obtain, up to this order, a very simple equation,
by construction, several terms
vanish and we obtain, up to this order, a very simple equation,
Is we write this in detail, substituting the expression for ![]() and
then using all the available symmetries in order to simplify the
expression (problem 1.3.1), in particular the fact
that the expectation values of odd powers of the field are zero due to
the fact that
and
then using all the available symmetries in order to simplify the
expression (problem 1.3.1), in particular the fact
that the expectation values of odd powers of the field are zero due to
the fact that ![]() is symmetrical by reflection of the fields, we
obtain
is symmetrical by reflection of the fields, we
obtain
This equation is simply the lattice version of the equation known as the
``tadpole'' equation in one-loop order. Since all the terms contain
at least one factor of ![]() , we may now cancel out one factor of
, we may now cancel out one factor of
![]() , which is the trivial
, which is the trivial ![]() solution which we mentioned
before, obtaining
solution which we mentioned
before, obtaining
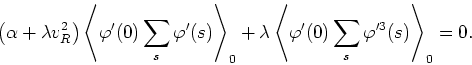
The calculation of the remaining expectation values involves only Gaussian integrals and we obtain for the first term (problem 1.3.2)
For the other expectation value we obtain (problem 1.3.3)
Observe how we avoided infrared problems in both cases, by the
introduction of the non-zero parameter ![]() . In these
calculations all the strong divergences due to the behavior of
. In these
calculations all the strong divergences due to the behavior of ![]() ,
which consist of terms proportional to
,
which consist of terms proportional to ![]() , cancel out. This fact
corresponds, in the usual language of the traditional approach to the
theory directly in the continuum, to the cancellation of the so-called
``vacuum bubbles'', and is a direct consequence of the fact that we are
expanding a ratio of two functional integrals. We have therefore for our
tadpole equation
, cancel out. This fact
corresponds, in the usual language of the traditional approach to the
theory directly in the continuum, to the cancellation of the so-called
``vacuum bubbles'', and is a direct consequence of the fact that we are
expanding a ratio of two functional integrals. We have therefore for our
tadpole equation
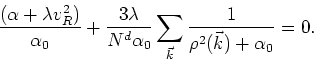
We recognize now that the sum over the momenta is our already well-known
quantity
![]() , the square of the width of the local
distribution of the fields in the measure of
, the square of the width of the local
distribution of the fields in the measure of ![]() . We obtain
therefore, substituting in terms of
. We obtain
therefore, substituting in terms of
![]() and cancelling the
factor of
and cancelling the
factor of ![]() ,
,
This equation gives us ![]() for small values of
for small values of ![]() and
and
![]() in the broken-symmetrical phase.
in the broken-symmetrical phase.
Let us consider here the issue of the dependence of this result on
![]() . Observe that the result does not depend explicitly on
. Observe that the result does not depend explicitly on
![]() , but it may depend on this parameter through the squared
width
, but it may depend on this parameter through the squared
width
![]() . For finite
. For finite ![]() the width does indeed depend on
the width does indeed depend on
![]() but, as was shows in the section
in [11], in the continuum limit it does not
depend on this parameter, so long as we make it go to zero sufficiently
fast. More precisely, it suffices that we make
but, as was shows in the section
in [11], in the continuum limit it does not
depend on this parameter, so long as we make it go to zero sufficiently
fast. More precisely, it suffices that we make
![]() , for some finite
, for some finite ![]() , for the limit
to be completely independent of the value of
, for the limit
to be completely independent of the value of ![]() . The mass parameter
. The mass parameter
![]() could even be chosen to have the same value as the renormalized
mass
could even be chosen to have the same value as the renormalized
mass ![]() of the model, but there is no need for this coming from this
calculation, all we know up to now is that
of the model, but there is no need for this coming from this
calculation, all we know up to now is that ![]() must be finite. Note
that the need to choose
must be finite. Note
that the need to choose ![]() dependent on
dependent on ![]() in a certain way in
order to make the results independent of
in a certain way in
order to make the results independent of ![]() is already a first
indication that the perturbative expansion is not completely
well-behaved, since there should be no dependence at all on
is already a first
indication that the perturbative expansion is not completely
well-behaved, since there should be no dependence at all on ![]() .
.
Going back to the analysis of the critical behavior of the model, if we
impose now that the only possible value for ![]() be zero, we
obtain from equation (1.3.4), by setting
be zero, we
obtain from equation (1.3.4), by setting ![]() in
it, the equation of the critical curve, to wit
in
it, the equation of the critical curve, to wit
where
![]() corresponds to the symmetrical
phase and
corresponds to the symmetrical
phase and
![]() to the broken-symmetrical
phase. We see that this equation has the same form of the heuristic
estimate that we proposed in section 1.1, differing from it only
by the numerical factor
to the broken-symmetrical
phase. We see that this equation has the same form of the heuristic
estimate that we proposed in section 1.1, differing from it only
by the numerical factor
![]() involved in the evaluation of
the relation between the width
involved in the evaluation of
the relation between the width ![]() of the local distribution and
the parameter
of the local distribution and
the parameter
![]() of the potential well. In other
words, the result coincides with our heuristic estimate if we choose for
the numerical constant
of the potential well. In other
words, the result coincides with our heuristic estimate if we choose for
the numerical constant ![]() introduced in that section the value
introduced in that section the value
![]() . We may now write our perturbative result for
. We may now write our perturbative result for ![]() in
terms of the expression in the equation of the critical line as
in
terms of the expression in the equation of the critical line as
which is only real in the broken-symmetrical phase, as expected, and
which shows explicitly how ![]() goes to zero when one approaches the
critical line from the broken-symmetrical phase.
goes to zero when one approaches the
critical line from the broken-symmetrical phase.
At this point it is important to point out, quite emphatically, that we
have just found one more worrisome property of the perturbative
approximation technique. We have found here a definite result for the
position of the critical curve for the model in a box with periodical
boundary conditions, for any value of ![]() , either finite or not. In
addition to this, this position of the critical curve has the curious
property of depending weakly on the irrelevant parameter
, either finite or not. In
addition to this, this position of the critical curve has the curious
property of depending weakly on the irrelevant parameter ![]() if
if
![]() is finite, and of becoming independent of the same parameter if
is finite, and of becoming independent of the same parameter if
![]() . Taken in this superficial way, our result seems to
indicate that, given a value of
. Taken in this superficial way, our result seems to
indicate that, given a value of ![]() , the system displays a
completely well-defined phase transition on finite lattices with
periodical boundary conditions.
, the system displays a
completely well-defined phase transition on finite lattices with
periodical boundary conditions.
However, it is a well-known fact that there is no possibility of
existence of a phase transition on finite lattices with periodical
boundary conditions in systems of the type that we are examining here. In
this kind of system, with couplings only between next-neighbors and
without external borders, the phase transition can be realized only in
the
![]() limit. We can only presume that the curious
dependence on
limit. We can only presume that the curious
dependence on ![]() for finite
for finite ![]() is somehow related to this
fact, effectively indicating, at best, that there can be a kind of
``approximate critical behavior'' for finite
is somehow related to this
fact, effectively indicating, at best, that there can be a kind of
``approximate critical behavior'' for finite ![]() . This is one more
circumstance in which we verify that this method of approximation has
rather singular properties and that it should only be used with the
greatest care.
. This is one more
circumstance in which we verify that this method of approximation has
rather singular properties and that it should only be used with the
greatest care.
A particularly interesting aspect of the structure of the model that we
can obtain from equation (1.3.5) is the slope
![]() of the critical curve near the
Gaussian point, which is given by
of the critical curve near the
Gaussian point, which is given by
We may ask here how close to the truth this result can be. Note that it
depends neither on ![]() nor on
nor on ![]() , and let us recall that the
dependence on
, and let us recall that the
dependence on ![]() vanishes in the continuum limit. Hence, if the
perturbative technique establishes at least a first-order approximation
for the result of the complete model, then this result should be exact at
the Gaussian point (problem 1.3.4). We will see
later on that it is consistent with the results obtained by means of
mean-field techniques and of stochastic simulations. In the case of the
stochastic simulations realized so far, it has been verified that it is
particularly difficult to execute them close to the Gaussian point, due
to the fact that in that region the potential wells of the model become
very shallow, which makes it more difficult to control the statistical
errors. Therefore, up to now it has not been possible to do more than to
confirm qualitatively this result with the stochastic simulations.
vanishes in the continuum limit. Hence, if the
perturbative technique establishes at least a first-order approximation
for the result of the complete model, then this result should be exact at
the Gaussian point (problem 1.3.4). We will see
later on that it is consistent with the results obtained by means of
mean-field techniques and of stochastic simulations. In the case of the
stochastic simulations realized so far, it has been verified that it is
particularly difficult to execute them close to the Gaussian point, due
to the fact that in that region the potential wells of the model become
very shallow, which makes it more difficult to control the statistical
errors. Therefore, up to now it has not been possible to do more than to
confirm qualitatively this result with the stochastic simulations.
Using the asymptotic values of
![]() in the dimensions
in the dimensions
![]() to
to ![]() , presented in the section in [11],
we obtain the results shown in table 1.3.1 for
the slope, where
, presented in the section in [11],
we obtain the results shown in table 1.3.1 for
the slope, where ![]() is the smaller angle that the tangent line to
the critical curve at the Gaussian point makes with the negative
is the smaller angle that the tangent line to
the critical curve at the Gaussian point makes with the negative ![]() semi-axis. It is interesting to observe that in the cases
semi-axis. It is interesting to observe that in the cases ![]() and
and
![]() , since
, since ![]() diverges, the slopes go to zero in the limit
and the critical curve collapse onto the negative
diverges, the slopes go to zero in the limit
and the critical curve collapse onto the negative ![]() semi-axis,
where the model does not exist because this semi-axis is part of the
unstable region. One might consider the interpretation that this is the
perturbative way of verifying that the
semi-axis,
where the model does not exist because this semi-axis is part of the
unstable region. One might consider the interpretation that this is the
perturbative way of verifying that the
![]() model does
not really exist as a quantum field theory for
model does
not really exist as a quantum field theory for ![]() .
.
Our next objective is to calculate the propagator of the model, which we will do first in the symmetrical phase. We will denote the dimensionless two-point function of the complete model by
To order zero we simply have that
![]() , where
, where
so that in this order we have the results of the free theory,
![]() and a simple pole with its residue equal to one
(apart from the normalization factor of
and a simple pole with its residue equal to one
(apart from the normalization factor of ![]() ) in the region of
imaginary momenta
) in the region of
imaginary momenta
![]() . Note that this
first-order result is not sufficient to allow us to take the continuum
limit, because we know that
. Note that this
first-order result is not sufficient to allow us to take the continuum
limit, because we know that ![]() must become negative in the limit,
while
must become negative in the limit,
while ![]() cannot be negative. In the next-order approximation,
using equation (1.2.3) up to first order, we will have
a result that we shall denote by
cannot be negative. In the next-order approximation,
using equation (1.2.3) up to first order, we will have
a result that we shall denote by
![]() , with
, with
and where
The expectation values that appear here are the zero-order propagator, as we calculated it before in the theory of the free field,
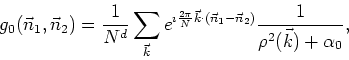
and the expectation values containing ![]() . The first one of these can
be easily calculated (problem 1.3.5) in terms of
expectation values that we have discussed and calculated before in the
sections in [12]
and [11], yielding
. The first one of these can
be easily calculated (problem 1.3.5) in terms of
expectation values that we have discussed and calculated before in the
sections in [12]
and [11], yielding
Observe that all the terms diverge strongly in the continuum limit,
containing factors of ![]() . The calculation of the last expectation
value (problem 1.3.6) is longer and, after some work,
we may write it in the form
. The calculation of the last expectation
value (problem 1.3.6) is longer and, after some work,
we may write it in the form
At this point we have everything written in terms of the propagator of
the free theory. Observe that here also we have terms with strong
divergences, involving factors of ![]() . The sums over position space
may be rewritten in momentum space and manipulated in such a way that,
when all the terms are brought together, one verifies that all the terms
with strong divergences cancel out, resulting in the final expression for
the first-order propagator in position space,
. The sums over position space
may be rewritten in momentum space and manipulated in such a way that,
when all the terms are brought together, one verifies that all the terms
with strong divergences cancel out, resulting in the final expression for
the first-order propagator in position space,
![\begin{eqnarray*}
g_{1}(\vec{n}_{1},\vec{n}_{2})=\frac{1}{N^d}\sum_{\vec{k}}
e^{...
...bda\sigma_{0}^{2}}
{[\rho^{2}(\vec{k})+\alpha_{0}]^{2}}\right\}.
\end{eqnarray*}](img283.gif)
The expression within braces is the form of the propagator in momentum
space. Observe that this time the result depends significantly on
![]() . On the other hand, we may use our freedom in principle, of
choosing
. On the other hand, we may use our freedom in principle, of
choosing ![]() in any way we wish within the stability bounds, in
order to simplify this expression, by eliminating the second term, which
contains a double pole. In order to do this is suffices to choose
in any way we wish within the stability bounds, in
order to simplify this expression, by eliminating the second term, which
contains a double pole. In order to do this is suffices to choose
We may do this only so long as the resulting ![]() remains
positive and so long as it goes to zero in the continuum limit. Examining
the expression in the right-hand side of this equation we recognize it as
the expression in the equation of the critical curve that we calculated
before, which shows that it does in fact go to zero in the
remains
positive and so long as it goes to zero in the continuum limit. Examining
the expression in the right-hand side of this equation we recognize it as
the expression in the equation of the critical curve that we calculated
before, which shows that it does in fact go to zero in the
![]() limit, so long as we take the limit in such a way
that the parameters of the theory approach the critical curve. We
therefore have here some perturbative evidence that the phase transition
of the model is indeed of second order and we see once more why it is
necessary to take the system to the critical situation in the continuum
limit. In addition to this, as we already discussed before in this
section, the expression in the right-hand side of the equation is
positive in the symmetrical phase, showing that
limit, so long as we take the limit in such a way
that the parameters of the theory approach the critical curve. We
therefore have here some perturbative evidence that the phase transition
of the model is indeed of second order and we see once more why it is
necessary to take the system to the critical situation in the continuum
limit. In addition to this, as we already discussed before in this
section, the expression in the right-hand side of the equation is
positive in the symmetrical phase, showing that ![]() will be
approaching zero by positive values and thus establishing the consistency
of this choice for
will be
approaching zero by positive values and thus establishing the consistency
of this choice for ![]() . Observe that, with this choice for
. Observe that, with this choice for
![]() , we may write the result for the propagator as
, we may write the result for the propagator as
that is, we get a propagator with form identical to that of the
propagator of the free theory, with a renormalized mass ![]() , where we
see that
, where we
see that
![]() and the renormalized mass is given by
and the renormalized mass is given by
Formally, we may try to understand the expression
![]() for the renormalized mass
parameter
for the renormalized mass
parameter ![]() as the sum of a zero-order term
as the sum of a zero-order term ![]() and a
first-order term proportional to
and a
first-order term proportional to ![]() . However, in truth this is
misleading, because we must recall that the parameter
. However, in truth this is
misleading, because we must recall that the parameter ![]() is in fact
negative in any continuum limit and hence that the first-order term
cannot be considered as a small correction to the situation in the theory
of the free field, in which
is in fact
negative in any continuum limit and hence that the first-order term
cannot be considered as a small correction to the situation in the theory
of the free field, in which ![]() must be positive. We see that, in
spite of the fact that we have developed this approximation technique in
the lines of an expansion in a perturbative series, the resulting object
has a character rather different from the expected.
must be positive. We see that, in
spite of the fact that we have developed this approximation technique in
the lines of an expansion in a perturbative series, the resulting object
has a character rather different from the expected.
We will see later on that the results of this process of approximation
for the renormalized mass agree surprisingly well with the results of the
stochastic simulations. In particular, note that the result indicates a
unit residue for the pole of the propagator, exactly as in the free
theory, ![]() being the only non-trivial parameter that appears.
This unit residue is also found in all the stochastic simulations, within
the statistical errors. Judging by the form of the propagator, one would
say that the spectrum of the theory seems to be that of free particles
with mass
being the only non-trivial parameter that appears.
This unit residue is also found in all the stochastic simulations, within
the statistical errors. Judging by the form of the propagator, one would
say that the spectrum of the theory seems to be that of free particles
with mass ![]() . One might consider interpreting this as an indirect
perturbative indication related to the underlying triviality of the
model. At least, the result for the residue is compatible with it.
. One might consider interpreting this as an indirect
perturbative indication related to the underlying triviality of the
model. At least, the result for the residue is compatible with it.
It is interesting to try to understand in clearer physical terms the
nature of the approximation technique that we have developed. The crucial
point for the success of the technique is the choice of ![]() ,
which ends up being equivalent to a preliminary implicit choice
,
which ends up being equivalent to a preliminary implicit choice
![]() , to be resolved after the end of the calculation,
a possibility that was suggested in section 1.2. From the very
beginning we are trying to approximate the expectation values of the
complete model by expectation values of a Gaussian model, which is
characterized by only two independent quantities, the expectation value
of the field
, to be resolved after the end of the calculation,
a possibility that was suggested in section 1.2. From the very
beginning we are trying to approximate the expectation values of the
complete model by expectation values of a Gaussian model, which is
characterized by only two independent quantities, the expectation value
of the field ![]() , which is related to the first-order moment
(observables with a single power of the field) of the statistical
distribution of the model, and the renormalized mass
, which is related to the first-order moment
(observables with a single power of the field) of the statistical
distribution of the model, and the renormalized mass ![]() , which is
related to the second-order moment (observables with two powers of the
field). In the case in which there is a non-vanishing
, which is
related to the second-order moment (observables with two powers of the
field). In the case in which there is a non-vanishing ![]() in the
complete model, the shift from the field
in the
complete model, the shift from the field ![]() to the field
to the field
![]() can be understood as a way to make identical the first-order
moments of the two distributions, that of the complete model and that of
the Gaussian model used for the approximation. In a similar way, the
choice
can be understood as a way to make identical the first-order
moments of the two distributions, that of the complete model and that of
the Gaussian model used for the approximation. In a similar way, the
choice
![]() can be understood as a way to make
identical the second-order moments of the two distributions. Both are
implicit conditions which are resolved in a self-consistent way at the
end of the calculations.
can be understood as a way to make
identical the second-order moments of the two distributions. Both are
implicit conditions which are resolved in a self-consistent way at the
end of the calculations.
We see therefore that what we are dealing with here is, much more than part of a perturbative expansion, a Gaussian approximation technique, which is not at all an expansion, but rather a single-step self-consistent type of approximation. Since the Gaussian does not have any moments with order greater than two, we cannot expect that this technique can be successfully used to approximate observables that are related to the higher moments of the distribution of the complete model. In particular, we should not expect that it will be useful to examine the issue of the renormalized coupling constant and the phenomenon of the interaction between particles within the structure of the quantum theory, which are related to the moments of order four and larger. In addition to this, we should not expect that it will be possible to improve on the results obtained here by the inclusion in the calculations of the terms of higher order of the expansion given in equation (1.2.3) since, when we adjust the only two independent moments existing in the Gaussian distribution so as to make them identical to the corresponding moments of the distribution of the complete model, we are already doing the best that can be done in terms of approximate a non-Gaussian distribution by a Gaussian distribution.
As our last objective in this section, we calculate the propagator of the
model in the broken-symmetrical phase. The calculations are all very
similar to the corresponding calculations in the symmetrical phase,
except for the need of the use in this case of the shifted field
![]() . In particular, in this case the same type of cancellation of
all the terms with strong divergences takes place. After some work
(problem 1.3.7) we obtain in this phase for the
first-order propagator, which we denote by
. In particular, in this case the same type of cancellation of
all the terms with strong divergences takes place. After some work
(problem 1.3.7) we obtain in this phase for the
first-order propagator, which we denote by
![]() , with
, with
the result
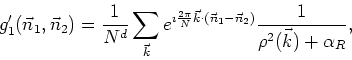
where the renormalized mass is now defined in terms of the dimensionless parameter
which is a positive quantity in this phase. Once again the expression in
the equation of the critical curve appears, showing once more that
![]() will go to zero when we approach this curve in the continuum
limit, this time by the other side, from the broken-symmetrical
phase. The factor of
will go to zero when we approach this curve in the continuum
limit, this time by the other side, from the broken-symmetrical
phase. The factor of ![]() that appears in this result confirms once more
our heuristic expectations and, as we will see later on, it also matches
with surprising precision the numerical results in this phase.
that appears in this result confirms once more
our heuristic expectations and, as we will see later on, it also matches
with surprising precision the numerical results in this phase.
Observe that, since
![]() is a function of
is a function of ![]() , both
this result and the result for the symmetrical phase are not explicit
solutions for
, both
this result and the result for the symmetrical phase are not explicit
solutions for ![]() but rather equations that determine
but rather equations that determine
![]() in an implicit way,
in an implicit way,
in the symmetrical phase and
in the broken-symmetrical phase, where
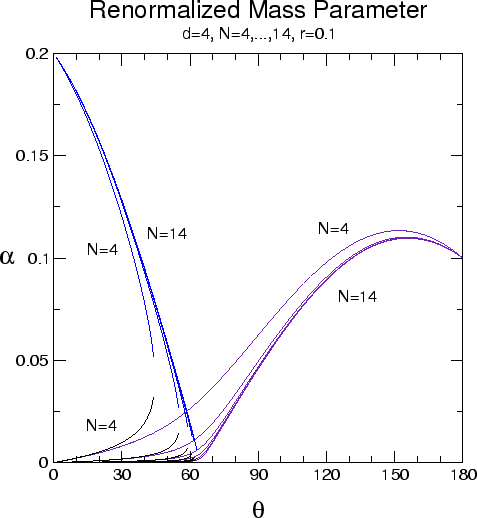 |
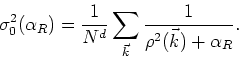
It is not difficult to determine the existence, the number and the
character of the solutions of these equations, if one separates from the
sum in
![]() the term containing the zero mode, and to find
these solutions on finite lattices by numerical means
(problems 1.3.8, 1.3.9,
1.3.10 and 1.3.11). We show in
figure 1.3.1 a graph with some of the numerical
solutions, illustrating their behavior for lattices of increasing size.
In this graph, instead of the usual Cartesian coordinates
the term containing the zero mode, and to find
these solutions on finite lattices by numerical means
(problems 1.3.8, 1.3.9,
1.3.10 and 1.3.11). We show in
figure 1.3.1 a graph with some of the numerical
solutions, illustrating their behavior for lattices of increasing size.
In this graph, instead of the usual Cartesian coordinates ![]() and
and
![]() in the parameter plane of the model, we use polar coordinates
centered at the Gaussian point, with the radius
in the parameter plane of the model, we use polar coordinates
centered at the Gaussian point, with the radius ![]() given by
given by
![]() , and the angle
, and the angle ![]() defined as the
angle between the radius vector
defined as the
angle between the radius vector
![]() and the negative
and the negative
![]() semi-axis.
semi-axis.
The equation for the symmetrical phase has two solutions, but only one of
them is positive and hence physically meaningful. While the positive
solution remains finite and non-vanishing in the
![]() limit, the negative solution becomes identically zero in the limit. Note
that this equation has solutions over the whole parameter plane and not
only in the symmetrical phase. The curves corresponding to this solution
are the ones with their maximums at the right in
figure 1.3.1. Of course this solution only has
meaning in the symmetrical phase, but since this is not a well-defined
concept on finite lattices, in order to determine the range of validity
of the solution on finite lattices, from the point of view of
perturbation theory, we must first discuss the solutions in the
broken-symmetrical phase. The equation for the broken-symmetrical phase
has two positive solutions, a small one and a large one, but only for
certain values of parameters, thus defining a perturbative
broken-symmetrical phase even on finite lattices. In the complementary
region of the parameter plane, which we might call the perturbative
symmetrical phase, the equation has no real solutions. On each finite
lattice the position of the curve separating these two regions can be
determined numerically, and we might call this curve the perturbative
critical curve. The small solution becomes identically zero in the
limit, the negative solution becomes identically zero in the limit. Note
that this equation has solutions over the whole parameter plane and not
only in the symmetrical phase. The curves corresponding to this solution
are the ones with their maximums at the right in
figure 1.3.1. Of course this solution only has
meaning in the symmetrical phase, but since this is not a well-defined
concept on finite lattices, in order to determine the range of validity
of the solution on finite lattices, from the point of view of
perturbation theory, we must first discuss the solutions in the
broken-symmetrical phase. The equation for the broken-symmetrical phase
has two positive solutions, a small one and a large one, but only for
certain values of parameters, thus defining a perturbative
broken-symmetrical phase even on finite lattices. In the complementary
region of the parameter plane, which we might call the perturbative
symmetrical phase, the equation has no real solutions. On each finite
lattice the position of the curve separating these two regions can be
determined numerically, and we might call this curve the perturbative
critical curve. The small solution becomes identically zero in the
![]() limit, showing that we should not attribute to it
any physical meaning. Once more this seems to be just a perturbative
ghost associated to an unstable solution sitting at the maximum that the
potential has at the origin. The curves corresponding to the large
solution are the ones with their maximums at the left in
figure 1.3.1.
limit, showing that we should not attribute to it
any physical meaning. Once more this seems to be just a perturbative
ghost associated to an unstable solution sitting at the maximum that the
potential has at the origin. The curves corresponding to the large
solution are the ones with their maximums at the left in
figure 1.3.1.
One can see that it is the large positive solutions in either phase that
carry the expected physical meaning by noting that for ![]() equal to
equal to
![]() we are over the positive
we are over the positive ![]() semi-axis and therefore
have the result for the free theory,
semi-axis and therefore
have the result for the free theory,
![]() , since in this
case
, since in this
case ![]() . For
. For ![]() close to
close to ![]() we approach the
negative
we approach the
negative ![]() semi-axis where, as we discussed before, the two
potential wells acquire a large separation from each other and the local
distribution of the fields sits at the minimum of one of them. As we saw
before, the minimum of the potential can then be approximated by a
parabola with a positive quadratic coefficient
semi-axis where, as we discussed before, the two
potential wells acquire a large separation from each other and the local
distribution of the fields sits at the minimum of one of them. As we saw
before, the minimum of the potential can then be approximated by a
parabola with a positive quadratic coefficient ![]() , and the model
once more approaches the free theory on finite lattices, with this new
value for the dimensionless mass parameter. As one can see in
figure 1.3.1 in this case the large solution does
indeed approach
, and the model
once more approaches the free theory on finite lattices, with this new
value for the dimensionless mass parameter. As one can see in
figure 1.3.1 in this case the large solution does
indeed approach
![]() as expected, where
as expected, where
![]() . Just as in the case
. Just as in the case
![]() the solution
seems to be exact in this case, because for
the solution
seems to be exact in this case, because for ![]() approaching
approaching ![]() we have a vanishing
we have a vanishing ![]() and the distribution tends to become
purely Gaussian, so that the Gaussian approximation tends to become a
perfect one. It is therefore to the two large solutions that we should
attribute physical meaning, using the broken-symmetrical solution where
it exists and using the symmetrical solution where the broken-symmetrical
solution does not exist, and therefore truncating in this way the
symmetrical solution. Note that there is a discontinuity between the two
solutions at the transition point, but this discontinuity vanishes in the
and the distribution tends to become
purely Gaussian, so that the Gaussian approximation tends to become a
perfect one. It is therefore to the two large solutions that we should
attribute physical meaning, using the broken-symmetrical solution where
it exists and using the symmetrical solution where the broken-symmetrical
solution does not exist, and therefore truncating in this way the
symmetrical solution. Note that there is a discontinuity between the two
solutions at the transition point, but this discontinuity vanishes in the
![]() limit. In this limit the edges of the two curves
approach the value
limit. In this limit the edges of the two curves
approach the value ![]() at the critical line.
at the critical line.
In the
![]() limit
limit
![]() becomes independent of
becomes independent of
![]() , the critical transition becomes completely well-defined and
the relations between
, the critical transition becomes completely well-defined and
the relations between ![]() and the parameters
and the parameters
![]() become linear, in either phase. If we define
become linear, in either phase. If we define
![]() , then we have in
the symmetrical phase
, then we have in
the symmetrical phase
and in the broken-symmetrical phase
which are equations of planes over the
![]() parameter
plane. The three-dimensional graph of
parameter
plane. The three-dimensional graph of
![]() over
the parameter plane is composed of pieces of two planes that intersect
within the
over
the parameter plane is composed of pieces of two planes that intersect
within the
![]() plane at the critical line. The first one
is a piece of the plane defined by the critical line and the line
plane at the critical line. The first one
is a piece of the plane defined by the critical line and the line
![]() within the vertical
within the vertical
![]() plane, the
second one is a piece of the plane defined by the critical line and the
line
plane, the
second one is a piece of the plane defined by the critical line and the
line
![]() in that same vertical
in that same vertical
![]() plane. The relevant part of the first plane is the part that stands over
the symmetrical phase, the relevant part of the second plane is the part
that stands over the broken-symmetrical phase.
plane. The relevant part of the first plane is the part that stands over
the symmetrical phase, the relevant part of the second plane is the part
that stands over the broken-symmetrical phase.
Note that both on finite lattices and in the
![]() limit
the perturbative solution for the expectation value
limit
the perturbative solution for the expectation value ![]() of the field
is proportional to the value of the renormalized mass in the
broken-symmetrical phase, that is, we have
of the field
is proportional to the value of the renormalized mass in the
broken-symmetrical phase, that is, we have
Due to the extra dependence on ![]() , we can have independent values
of the two dimensionless renormalized quantities,
, we can have independent values
of the two dimensionless renormalized quantities, ![]() and
and
![]() . Whether or not the same is true for the corresponding
dimensionfull quantities
. Whether or not the same is true for the corresponding
dimensionfull quantities ![]() and
and ![]() depends on the dimension
depends on the dimension ![]() of space-time, because the dimensions of the field and therefore of
of space-time, because the dimensions of the field and therefore of
![]() depend on it (problem 1.3.12).
depend on it (problem 1.3.12).
The final conclusion of this effort is that the perturbative technique of
Gaussian approximation allows us to calculate in a useful way the
observables related to the aspects of propagation of particles and to the
aspects of spontaneous symmetry breaking in the quantum theory of the
![]() model. As we shall see later on, these results are
surprisingly precise in some cases and, by and large, give us a
qualitatively correct picture of the critical behavior of the model. On
the other hand, it is doubtful that the technique can be extended in an
effective way to other observables and aspects of the model. As far as
one can verify up to this point, the model seems to contain particles of
mass
model. As we shall see later on, these results are
surprisingly precise in some cases and, by and large, give us a
qualitatively correct picture of the critical behavior of the model. On
the other hand, it is doubtful that the technique can be extended in an
effective way to other observables and aspects of the model. As far as
one can verify up to this point, the model seems to contain particles of
mass ![]() , which we may adjust freely, in addition to being able to
generate a non-vanishing expectation value
, which we may adjust freely, in addition to being able to
generate a non-vanishing expectation value
![]() for the dimensionless field. In the continuum limit
for the dimensionless field. In the continuum limit ![]() vanishes,
since we must approach the critical curve where the phase transition is
of second order, with
vanishes,
since we must approach the critical curve where the phase transition is
of second order, with ![]() over the curve, but it is possible to
adjust things so that the dimensionfull field has a non-vanishing
expectation value
over the curve, but it is possible to
adjust things so that the dimensionfull field has a non-vanishing
expectation value
![]() in the limit
(problem 1.3.12). Hence, up to this point the model
seems to contain only the phenomena of propagation and of spontaneous
symmetry breaking. Whether or not it contains anything beyond this is an
issue for further exploration and discussion
(problems 1.3.13 and 1.3.14).
in the limit
(problem 1.3.12). Hence, up to this point the model
seems to contain only the phenomena of propagation and of spontaneous
symmetry breaking. Whether or not it contains anything beyond this is an
issue for further exploration and discussion
(problems 1.3.13 and 1.3.14).
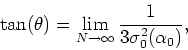
where ![]() is the angle between the negative
is the angle between the negative ![]() semi-axis and
the tangent to the critical curve at the Gaussian point.
semi-axis and
the tangent to the critical curve at the Gaussian point.
were we recall that
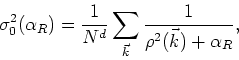
has a single positive solution for each pair of values
![]() in the stable region of the parameter plane of the model. In order to do
this, remember that the parameter
in the stable region of the parameter plane of the model. In order to do
this, remember that the parameter ![]() has to be positive or zero
and consider the behavior of the left side of the equation when
has to be positive or zero
and consider the behavior of the left side of the equation when
![]() and when
and when
![]() .
Remember that the sum that defines the quantity
.
Remember that the sum that defines the quantity
![]() includes
the zero mode and write it as
includes
the zero mode and write it as
where
![]() has a finite limit for
has a finite limit for
![]() .
Show also that there is a second solution, which is negative (and hence
destitute of any physical meaning) and which becomes identically zero in
the
.
Show also that there is a second solution, which is negative (and hence
destitute of any physical meaning) and which becomes identically zero in
the
![]() limit.
limit.
for
![]() .
.
has two different real and positive solutions for some pairs of values
![]() in the stable region of the parameter plane of the
model, and no real solutions for other pairs of values. Use the same
ideas and techniques that were suggested in
problem 1.3.8. Show that the condition on
in the stable region of the parameter plane of the
model, and no real solutions for other pairs of values. Use the same
ideas and techniques that were suggested in
problem 1.3.8. Show that the condition on ![]() and
and ![]() for the existence of solutions can be written in an
implicit way, which depends on
for the existence of solutions can be written in an
implicit way, which depends on ![]() on finite lattices, as
on finite lattices, as
and interpret the meaning of this condition on the continuum limit. Show
that when the equality holds in the condition above the renormalized mass
parameter is given by
![]() , and hence that
it goes to zero at the critical curve in the continuum limit. Show also
that the smaller of the two solutions becomes identically zero in the
, and hence that
it goes to zero at the critical curve in the continuum limit. Show also
that the smaller of the two solutions becomes identically zero in the
![]() limit.
limit.
for
![]() .
.
where the sum ![]() is given in terms of the free propagator by
is given in terms of the free propagator by