Next: Perturbation Theory Up: The Polynomial Model Previous: The Polynomial Model Contents
In the previous volume of this series [2] we studied in detail the theory of the free scalar field. That model was sufficiently simple to allow us to calculate analytically all the predictions of the theory. As we saw, both in the case of the classical theory and in the case of the quantum theory this simplicity follows from the linearity of the model. We also saw that this same linearity is responsible for the fact that the model does not contain the concept of interactions between particles, and hence that the only physics that it does contain is the propagation of free particles. This was shown by the factorization of all the correlation functions in terms of the propagator, and also by the fact that the energies of the particles are simply additive, that is, the energy of a state containing two particles is the sum of the energies of the two corresponding single-particle states, implying the absence of any kind of interaction energy.
We will make here a first trial at including interactions in the theory, for which it will be necessary to break the linearity of the model, including in the action terms with more that two powers of the field. We will therefore examine the model defined by
which we denominate the
![]() polynomial model. We
therefore choose to break the linearity of the model by the introduction
of a new ultra-local term into the action, leaving untouched the term
containing the derivatives. This is the simplest example of a model that,
in the classical theory, contains interacting fields. Our task here is to
determine the nature of the corresponding quantum theory. This new action
still has the same symmetry of the action of the free theory, namely, it
is invariant by the sign inversion of the fields. In addition to this, it
has a lower bound so long as the parameter
polynomial model. We
therefore choose to break the linearity of the model by the introduction
of a new ultra-local term into the action, leaving untouched the term
containing the derivatives. This is the simplest example of a model that,
in the classical theory, contains interacting fields. Our task here is to
determine the nature of the corresponding quantum theory. This new action
still has the same symmetry of the action of the free theory, namely, it
is invariant by the sign inversion of the fields. In addition to this, it
has a lower bound so long as the parameter ![]() , which we call the
coupling constant, is positive and not zero. On the other hand, unlike
what happened in the case of the free theory, the parameter
, which we call the
coupling constant, is positive and not zero. On the other hand, unlike
what happened in the case of the free theory, the parameter ![]() may
be negative in this model, so long as
may
be negative in this model, so long as ![]() satisfies these
conditions.
satisfies these
conditions.
Note that the addition to the action of the free theory of a single cubic
term is out of the question for two reasons: it would break the symmetry
and, more importantly, would cause the action not to have a lower bound.
This second problem is much more serious than the failure of the action
to be invariant by the symmetry transformations, since it would imply the
non-existence of the corresponding quantum theory. We could, on the other
hand, include a cubic term together with the quartic term, thus obtaining
a non-symmetrical but stable theory. If we want to have a stable theory
and keep the symmetry, we should restrict the discussion to terms with
even powers of the field. We will do this here, for simplicity and ease
of presentation, and motivated by the fact that, in general, symmetries
have an important role to play in physics. We will discuss explicitly the
case ![]() , but almost everything that we will do can also be
done for the cases
, but almost everything that we will do can also be
done for the cases ![]() ,
,
![]() , with analogous
results.
, with analogous
results.
We say, in the classical theory defined by the action given above, that
the field ![]() is self-interacting. As we may see in future
volumes of this series, it is also possible to define models with fields
having several components that interact with each other, and that involve
invariance by groups of symmetry transformations which are larger and
more complex than the simple sign reflections that we have in the model
with a single component. It is also possible to define manageable models
with different types of field that interact with one another, which are,
of course, the most important models for real physics. However, for our
objectives here we may limit ourselves to the model with a single field
component, postponing to a future opportunity the discussion of the more
complex models.
is self-interacting. As we may see in future
volumes of this series, it is also possible to define models with fields
having several components that interact with each other, and that involve
invariance by groups of symmetry transformations which are larger and
more complex than the simple sign reflections that we have in the model
with a single component. It is also possible to define manageable models
with different types of field that interact with one another, which are,
of course, the most important models for real physics. However, for our
objectives here we may limit ourselves to the model with a single field
component, postponing to a future opportunity the discussion of the more
complex models.
Unlike what happened in the case of the free field, in the non-linear models there is no known way to calculate the predictions of the quantum theory in exact analytical form. In this section we will limit ourselves to the qualitative description of the behavior of the model by means of heuristic arguments based on extensive experience with its numerical treatment. Later on we will develop a technique of approximate perturbative calculations that will allow us to determine in a quantitative and fairly reliable way some of the main characteristics of the model. In general, in the case of the non-linear models it will always be necessary to make use of some approximation technique or of computer simulations in order to determine the behavior of the models.
In our approach to the subject, the computer simulations will often be the main tool for the exploration of the models. Once one becomes well acquainted with the technique of stochastic simulation, it can become a language for the understanding of the models, sometimes leading one to the solution of problems, sometimes suggesting new ideas, new observables and even new models. The ideas and techniques involved in the methods of stochastic simulation constitute a rather extended topic with a very technical character, and will be developed in detail in a separate volume of this small series of books.
The character of the classical theory determined by our action is clear,
and it is not necessary to examine it in detail. The definition of the
classical theory is the same as before, the classical solution is the
configuration ![]() that minimizes the action. The fact that it
exists is guaranteed by the conditions we impose on the parameters of the
model:
that minimizes the action. The fact that it
exists is guaranteed by the conditions we impose on the parameters of the
model: ![]() with any
with any ![]() or
or ![]() with
with ![]() .
We may derive, in a way analogous to the one used before for the free
theory, the corresponding classical equation of motion, which will be, of
course, a non-linear differential equation for
.
We may derive, in a way analogous to the one used before for the free
theory, the corresponding classical equation of motion, which will be, of
course, a non-linear differential equation for ![]() (problem 1.1.1). In order to begin the examination of
the behavior of the quantum theory, we recall that it is defined by the
probability distribution over all possible configurations of
(problem 1.1.1). In order to begin the examination of
the behavior of the quantum theory, we recall that it is defined by the
probability distribution over all possible configurations of ![]() ,
given by
,
given by
![\begin{displaymath}
\frac{\displaystyle [{\bf
d}\varphi]\:e^{-\sum_{\ell}\frac{1...
...{\alpha}{2}\varphi^{2}+
\frac{\lambda}{4}\varphi^{4}\right)}},
\end{displaymath}](img30.gif)
 |
where we grouped separately the term containing the derivatives and the
ultra-local part, containing the polynomial terms, both the quadratic one
and the quartic one, which we call the interaction term. If we recall
that the measure
![]() is a product of differentials over
all the sites
is a product of differentials over
all the sites ![]() , representing the fact that in this measure the
stochastic variables
, representing the fact that in this measure the
stochastic variables ![]() have uniform probability distributions, we
see that we can include the ultra-local terms in the measure, writing the
distribution as
have uniform probability distributions, we
see that we can include the ultra-local terms in the measure, writing the
distribution as
![\begin{displaymath}
\frac{\displaystyle \left[{\bf d}\varphi\;e^{-\left(\frac{\a...
...ght]
\:e^{-\sum_{\ell}\frac{1}{2}(\Delta_{\ell}\varphi)^{2}}}.
\end{displaymath}](img34.gif)
In this new measure the variables ![]() no longer have uniform
probability distributions, but have instead the probability distribution
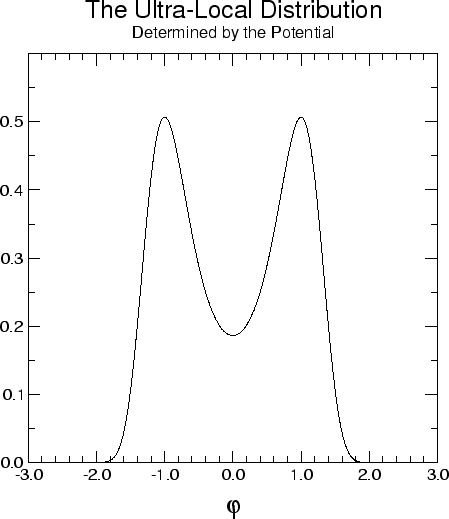
given by the exponential of the potential. A typical example of such a
distribution can be seen in figure 1.1.1. We
see in this way that a possible way to understand our model is to think
of it as constituted of the dynamics implemented by the derivative term,
but applied indirectly to new random variables
no longer have uniform
probability distributions, but have instead the probability distribution
given by the exponential of the potential. A typical example of such a
distribution can be seen in figure 1.1.1. We
see in this way that a possible way to understand our model is to think
of it as constituted of the dynamics implemented by the derivative term,
but applied indirectly to new random variables ![]() located at the
sites, with uniform probability distributions, which are given in terms
of the variables
located at the
sites, with uniform probability distributions, which are given in terms
of the variables ![]() by the differential relation
by the differential relation
This means that we may write the stochastic variable ![]() , which has an
uniform probability distribution within a closed interval, in terms of
the stochastic variable
, which has an
uniform probability distribution within a closed interval, in terms of
the stochastic variable ![]() , which has a non-uniform probability
distribution over the whole real line, as
, which has a non-uniform probability
distribution over the whole real line, as
In this way the theory is reduced to the study of the effect of the
derivative term on the local distributions of either ![]() or
or ![]() at each site. The inverse of relation (1.1.2), which
usually can only be obtained numerically, gives us
at each site. The inverse of relation (1.1.2), which
usually can only be obtained numerically, gives us ![]() and
enables us to obtain
and
enables us to obtain ![]() with the correct non-uniform distribution,
starting from the variable
with the correct non-uniform distribution,
starting from the variable ![]() with an uniform probability
distribution within a closed interval, which is not difficult to generate
numerically. In this way a part of the structure of the model, the part
of the distribution given by the ultra-local terms of the action, is
implemented in an exact way. This is, in fact, one of the ways in which
one can simulate this model in practice, by producing values of
with an uniform probability
distribution within a closed interval, which is not difficult to generate
numerically. In this way a part of the structure of the model, the part
of the distribution given by the ultra-local terms of the action, is
implemented in an exact way. This is, in fact, one of the ways in which
one can simulate this model in practice, by producing values of ![]() at
each site with the correct distribution, getting from them the
corresponding values of
at
each site with the correct distribution, getting from them the
corresponding values of ![]() , and simulating the dynamics of the
derivative term by the use of stochastic techniques. The use in
stochastic simulations is the main application of this decomposition,
which usually is not very useful as an analytical approach.
, and simulating the dynamics of the
derivative term by the use of stochastic techniques. The use in
stochastic simulations is the main application of this decomposition,
which usually is not very useful as an analytical approach.
In a very general way, the complete local distribution that rules the fluctuating values assumed by the fields at an arbitrarily given site is given by the combination of the effects of the potential and of the derivative term. In order to discuss the behavior of the model at an intuitive level, it is very useful to invert the decomposition described above, representing the effect of the derivative term by the Gaussian local distribution that it implies, which was studied in detail in the first volume of this series of books, and considering directly the effects that the potential term may have on it. This allows us to use in the analysis of the model our classical intuition concerning the behavior of an object within the potential, by extending the object from a simple point body to a fluctuating statistical distribution. In this way we are able to build an almost-classical intuition in order to understand the behavior of the model.
We can imagine that we draw a copy of the potential at each site and that
we put inside it the value of the field at that site, while the terms
![]() interconnect each pair of neighboring sites.
The stochastic dynamics implemented by these derivative terms will cause
the values of the fields to fluctuate at each site, so that we will
actually have a distribution of values within each potential. In the
theory of the free field these local distributions are simple Gaussians,
whose width
interconnect each pair of neighboring sites.
The stochastic dynamics implemented by these derivative terms will cause
the values of the fields to fluctuate at each site, so that we will
actually have a distribution of values within each potential. In the
theory of the free field these local distributions are simple Gaussians,
whose width ![]() is a number of the order of
is a number of the order of ![]() for any lattice
size, a number that determines the value of the physical mass (also
called the renormalized mass), which in the case of the free theory is
simply
for any lattice
size, a number that determines the value of the physical mass (also
called the renormalized mass), which in the case of the free theory is
simply ![]() . In our current model the complete local
distributions also have a width
. In our current model the complete local
distributions also have a width
![]() of the order of
of the order of
![]() , but their format may no longer be exactly Gaussian. The renormalized
mass is defined in this model, just as in the free theory, as the inverse
of the correlation length of the model, measured through the two-point
correlation function, and presumably it is also related to
, but their format may no longer be exactly Gaussian. The renormalized
mass is defined in this model, just as in the free theory, as the inverse
of the correlation length of the model, measured through the two-point
correlation function, and presumably it is also related to ![]() , as
is the case for the free theory. What we propose to do in this section is
to understand the complete dynamics of the model by considering directly
the influence of the potential over the Gaussian local distribution
implemented by the derivative term.
, as
is the case for the free theory. What we propose to do in this section is
to understand the complete dynamics of the model by considering directly
the influence of the potential over the Gaussian local distribution
implemented by the derivative term.
Let us recall that the relation between the two-point function and the
renormalized mass was studied in detail, in the case of the free field,
in a section of the first volume [4]. The
exponential decay of the two-point function for large distances ![]() ,
given by
,
given by ![]() as was studied in that section, is a general
property of all massive theories, either free or otherwise. The behavior
of the two-point function of the interacting theories for large distances
is in general of this same type, except for the exchange of the parameter
as was studied in that section, is a general
property of all massive theories, either free or otherwise. The behavior
of the two-point function of the interacting theories for large distances
is in general of this same type, except for the exchange of the parameter
![]() for another parameter
for another parameter ![]() which usually differs from
which usually differs from ![]() .
In the numerical approach we usually measure this new parameter by means
of a curve-fitting process applied to the numerical propagator of the
theory in momentum space rather than position space, that is, to the
Fourier transform of the two-point function, which is technically easier
to do, and also more efficient. We do this in the expectation, to be
confirmed a posteriori, that the form of this function in the interacting
models is not very different from its format in the free theory, and it
usually works very well.
.
In the numerical approach we usually measure this new parameter by means
of a curve-fitting process applied to the numerical propagator of the
theory in momentum space rather than position space, that is, to the
Fourier transform of the two-point function, which is technically easier
to do, and also more efficient. We do this in the expectation, to be
confirmed a posteriori, that the form of this function in the interacting
models is not very different from its format in the free theory, and it
usually works very well.
In the model that we are introducing here, given values of ![]() ,
, ![]() and
and ![]() , we will have not only a resulting value for the parameter
, we will have not only a resulting value for the parameter
![]() related to the renormalized mass, but also some resulting
value for the renormalized coupling constant
related to the renormalized mass, but also some resulting
value for the renormalized coupling constant ![]() , which
is the physical coupling constant whose nature and precise definition we
will examine in more detail later on. Unlike what happened in the free
theory, in general
, which
is the physical coupling constant whose nature and precise definition we
will examine in more detail later on. Unlike what happened in the free
theory, in general ![]() will not be equal to
will not be equal to ![]() , and in
addition to this neither will
, and in
addition to this neither will ![]() be equal do
be equal do ![]() . In
fact, let us recall the fact that the parameter
. In
fact, let us recall the fact that the parameter ![]() can be negative
in this model, while the parameter
can be negative
in this model, while the parameter
![]() is
necessarily non-negative, and should tend to zero in the continuum limit.
The rule of the game now is that neither
is
necessarily non-negative, and should tend to zero in the continuum limit.
The rule of the game now is that neither ![]() nor
nor ![]() have any
direct physical meaning and that we are free to do with them whatever is
necessary, within the constraints of the stability of the theory, in
order to have
have any
direct physical meaning and that we are free to do with them whatever is
necessary, within the constraints of the stability of the theory, in
order to have ![]() and
and ![]() assume physically acceptable
and significant values in the limit
assume physically acceptable
and significant values in the limit
![]() .
.
Since we have two free parameters to adjust in the model, that is, two
functions ![]() and
and ![]() of the increasing size
of the increasing size ![]() of the
lattice that we may define, it may seem at first sight that we may always
choose these functions so as to obtain any physically acceptable values
of
of the
lattice that we may define, it may seem at first sight that we may always
choose these functions so as to obtain any physically acceptable values
of
![]() and
and
![]() in
the limit
in
the limit
![]() . However, this is not necessarily so
because, besides the stability constraints that we must impose on the
basic parameters of the theory, it may be that the dynamics of the theory
itself imposes over the renormalized parameters
. However, this is not necessarily so
because, besides the stability constraints that we must impose on the
basic parameters of the theory, it may be that the dynamics of the theory
itself imposes over the renormalized parameters ![]() and
and
![]() other constraints, with the consequence that not all the
possibilities are actually realized in practice. In an extreme case, it
is possible that there are no choices of the functions
other constraints, with the consequence that not all the
possibilities are actually realized in practice. In an extreme case, it
is possible that there are no choices of the functions ![]() and
and ![]() for which the values of
for which the values of ![]() and
and ![]() are physically acceptable in the limit, in which case we say that the
quantum theory of the model does not exist. In a more general way,
it may be that not all pairs of physically acceptable values for
are physically acceptable in the limit, in which case we say that the
quantum theory of the model does not exist. In a more general way,
it may be that not all pairs of physically acceptable values for
![]() and
and ![]() are reachable by means of some path
are reachable by means of some path
![]() with increasing
with increasing ![]() , in the space of parameters
of the theory. For example, it may be that a constraint between
, in the space of parameters
of the theory. For example, it may be that a constraint between
![]() and
and ![]() is established in the limit, preventing us
from choosing both of them freely, in which case we may say that the
parameters
is established in the limit, preventing us
from choosing both of them freely, in which case we may say that the
parameters ![]() and
and ![]() become degenerate in the limit.
become degenerate in the limit.
In what follows we will describe a qualitative way of understanding the
behavior of the model which, despite the fact that it is purely intuitive
and heuristic, based on the phenomenology of computer simulations, will
give us qualitatively correct results, as we will verify later on by
means of approximate calculations1.1. In order
to do this we will, as was mentioned above, represent the effect of the
derivative term of the action by the fluctuations that it implies for the
values of the field ![]() at a given site, resulting on a Gaussian
local distribution of values with a width of the order of
at a given site, resulting on a Gaussian
local distribution of values with a width of the order of ![]() . Let us
recall that in the case of the free field the width
. Let us
recall that in the case of the free field the width ![]() did not
depend on
did not
depend on ![]() in the continuum limit. On finite lattices the width
did depend on
in the continuum limit. On finite lattices the width
did depend on ![]() , but not very strongly, so long as
, but not very strongly, so long as
![]() was not zero on finite lattices. In an analogous way, in our
case here we expect the width
was not zero on finite lattices. In an analogous way, in our
case here we expect the width ![]() not to depend on
not to depend on ![]() in the
limit, while on finite lattices it should not depend too strongly on
either
in the
limit, while on finite lattices it should not depend too strongly on
either ![]() or
or ![]() .
.
 |
In this way, in first approximation we may imagine that the width of the
local distribution behaves like a semi-rigid body with finite dimensions
which are almost constant along the continuum limit. If the width is
``squeezed'' to any value below its normal size, this gives rise to a
non-zero value for the renormalized mass ![]() . A zero squeezing force
corresponds to zero
. A zero squeezing force
corresponds to zero ![]() , and the larger the squeeze, the larger the
renormalized mass. As the lattice size
, and the larger the squeeze, the larger the
renormalized mass. As the lattice size ![]() increases the width becomes
more ``rigid'', in the sense that the same squeezing force corresponds to
a larger value of
increases the width becomes
more ``rigid'', in the sense that the same squeezing force corresponds to
a larger value of ![]() , until it becomes infinitely rigid in the
continuum limit, in which any non-zero squeezing force gives rise to an
infinite
, until it becomes infinitely rigid in the
continuum limit, in which any non-zero squeezing force gives rise to an
infinite ![]() . Let us imagine now that we insert this local
distribution inside the potential defined by the ultra-local terms of the
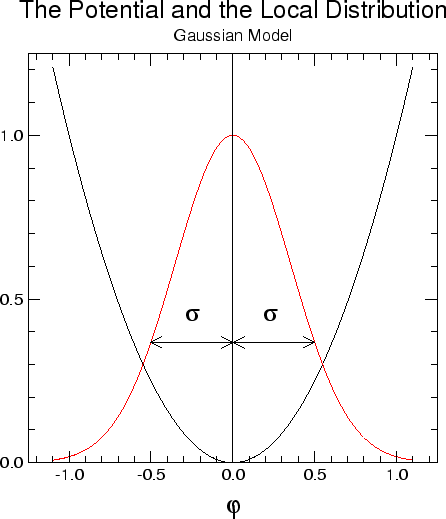
action at each site, as shown in
figure 1.1.2 for the case of the free
theory, with a Gaussian distribution and a quadratic potential. If we
were examining the classical theory, we would put inside the potential a
point body representing the value of the classical solution for the
field, and it would come to rest at the minimum of the potential. The
examination of the behavior of the quantum theory corresponds to the
introduction into the potential well of an extended object which can be
represented heuristically by our semi-rigid body, which becomes rigid in
the continuum limit in the sense explained above.
. Let us imagine now that we insert this local
distribution inside the potential defined by the ultra-local terms of the
action at each site, as shown in
figure 1.1.2 for the case of the free
theory, with a Gaussian distribution and a quadratic potential. If we
were examining the classical theory, we would put inside the potential a
point body representing the value of the classical solution for the
field, and it would come to rest at the minimum of the potential. The
examination of the behavior of the quantum theory corresponds to the
introduction into the potential well of an extended object which can be
represented heuristically by our semi-rigid body, which becomes rigid in
the continuum limit in the sense explained above.
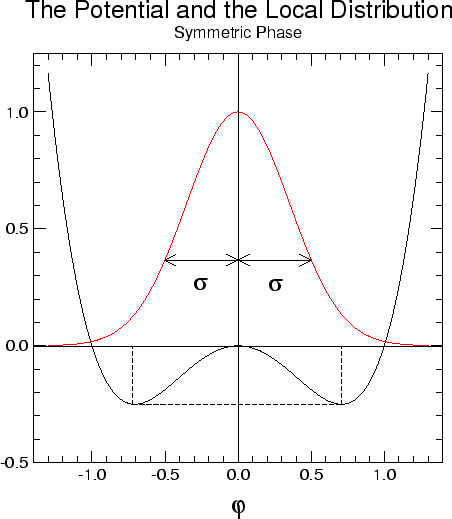 |
The width of the local distribution in the absence of the potential is
determined only by the derivative term and corresponds to the value
![]() , that is, to a zero renormalized mass. When we put the
distribution under the action of the potential on a finite lattice what
happens is that it tends to concentrate the values of the field around
the minimum, and hence squeezes the distribution, decreasing its width,
because it is statistically unfavorable for the field to exist in the
positions where the potential is larger. This squeeze of the width of the
distribution gives rise to a finite and non-zero value for
, that is, to a zero renormalized mass. When we put the
distribution under the action of the potential on a finite lattice what
happens is that it tends to concentrate the values of the field around
the minimum, and hence squeezes the distribution, decreasing its width,
because it is statistically unfavorable for the field to exist in the
positions where the potential is larger. This squeeze of the width of the
distribution gives rise to a finite and non-zero value for ![]() and hence for the renormalized mass. The decrease in the width of the
distribution is never very large, and it is still a quantity of the order
of
and hence for the renormalized mass. The decrease in the width of the
distribution is never very large, and it is still a quantity of the order
of ![]() . The difference in width due to the squeeze goes to zero in the
continuum limit because, as we saw in the first volume of this series, in
this limit it is necessary that
. The difference in width due to the squeeze goes to zero in the
continuum limit because, as we saw in the first volume of this series, in
this limit it is necessary that ![]() go to zero in the free
theory, making the potential well become infinitely wide and flat at the
position of the minimum. The fact is that such a vanishing effect over
the width is sufficient to give to the renormalized mass, in the limit,
any positive value we wish.
go to zero in the free
theory, making the potential well become infinitely wide and flat at the
position of the minimum. The fact is that such a vanishing effect over
the width is sufficient to give to the renormalized mass, in the limit,
any positive value we wish.
 |
In our model with a quartic term, in the case where we have both ![]() and
and ![]() positive or zero, we should expect a qualitatively similar
behavior, since we have the same derivative term in the action and a
potential well with a similar form, although the detailed format of the
curve is not exactly the same. In this case, in order for the potential
well to become infinitely wide in the continuum limit, thus allowing
positive or zero, we should expect a qualitatively similar
behavior, since we have the same derivative term in the action and a
potential well with a similar form, although the detailed format of the
curve is not exactly the same. In this case, in order for the potential
well to become infinitely wide in the continuum limit, thus allowing
![]() to go to zero and
to go to zero and ![]() to approach a finite value, it is
necessary that both
to approach a finite value, it is
necessary that both ![]() and
and ![]() tend to zero in the limit. In
this way we have just made, without too much effort, a prediction with
very serious consequences regarding the behavior of the model: if we
limit ourselves to the case in which
tend to zero in the limit. In
this way we have just made, without too much effort, a prediction with
very serious consequences regarding the behavior of the model: if we
limit ourselves to the case in which ![]() and
and ![]() for all
for all ![]() , it will be necessary to make both
, it will be necessary to make both
![]() and
and
![]() in the limit, which takes the model back to
the critical point of the Gaussian model and therefore eliminates any
possibility that
in the limit, which takes the model back to
the critical point of the Gaussian model and therefore eliminates any
possibility that ![]() be different from zero in limits of this
type.
be different from zero in limits of this
type.
Except for the case ![]() , this implies that there are in fact no
interactions between particles in the quantum theory of this model, in
any limits that stay within the quadrant given by
, this implies that there are in fact no
interactions between particles in the quantum theory of this model, in
any limits that stay within the quadrant given by ![]() and
and
![]() . We say that in this case the model has only the trivial limit, leading to the theory of the free field, or that the
theory is trivial in this sector of the space of parameters of the
model. The case
. We say that in this case the model has only the trivial limit, leading to the theory of the free field, or that the
theory is trivial in this sector of the space of parameters of the
model. The case ![]() is a little different because, since in this case
the physical coupling constant has dimensions of mass, it is possible
that there are interactions even if the model approaches the Gaussian
point, e phenomenon that we will discuss later on.
is a little different because, since in this case
the physical coupling constant has dimensions of mass, it is possible
that there are interactions even if the model approaches the Gaussian
point, e phenomenon that we will discuss later on.
We conclude that, if we are to have any chance of finding an interesting
limit in this model, it will be necessary for at least one of the two
parameters to be negative. Since we cannot make ![]() negative due to
the stability constraints, it follows that the parameter
negative due to
the stability constraints, it follows that the parameter ![]() fill be necessarily negative, in any continuum limit of this model that
has any chance of not being trivial. In fact, in this case something very
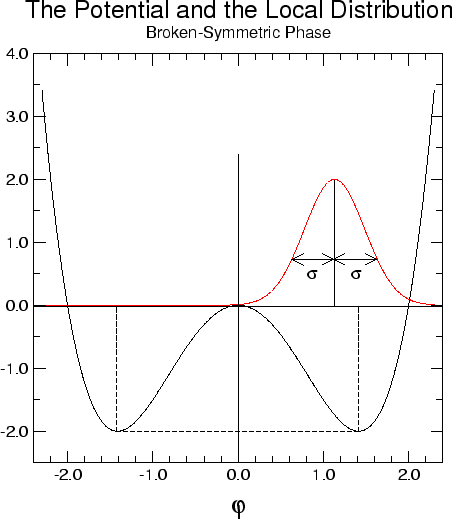
interesting happens, because the potential of the model acquires a double
well, as shown in figure 1.1.3, which alters
completely the behavior of the model, since now a new relevant parameter
related to the potential arises, given by the distance between the two
minima, which can be easily calculated from the potential. We see that we
now have two different widths at play in the problem, the width of the
local distribution and the distance between the two minima. We also have
two widths related to the potential, the width of each one of the two
wells and the total width of the two wells, which are related by a factor
of approximately two. The positions of the two minima of the potential
are given by
fill be necessarily negative, in any continuum limit of this model that
has any chance of not being trivial. In fact, in this case something very
interesting happens, because the potential of the model acquires a double
well, as shown in figure 1.1.3, which alters
completely the behavior of the model, since now a new relevant parameter
related to the potential arises, given by the distance between the two
minima, which can be easily calculated from the potential. We see that we
now have two different widths at play in the problem, the width of the
local distribution and the distance between the two minima. We also have
two widths related to the potential, the width of each one of the two
wells and the total width of the two wells, which are related by a factor
of approximately two. The positions of the two minima of the potential
are given by
![]() , while the value of the
potential at the minima is given by
, while the value of the
potential at the minima is given by
![]() .
.
We see at once that now the statistical disadvantage of the rise of the
potential at each side of the double well, which tend to squeeze the
distribution, can be compensated by the statistical advantage due to the
two local minima of the potential, which may tend to widen the
distribution. Another way to put it is to say that the central bump of
the potential tends to ``un-squeeze'' the distribution, working against
the squeezing tendency of the potential rises at the two sides of the
double well. If we tune our parameters in an appropriate way, it may be
possible to end up with a vanishing squeeze in the limit, without the
need for an infinitely wide well. In this way the possibility arises that
we may have in this case ![]() without it being necessary that
without it being necessary that
![]() or
or ![]() approach zero in the continuum limit. In other
words, the possibility arises that there are certain non-zero pairs of
values
approach zero in the continuum limit. In other
words, the possibility arises that there are certain non-zero pairs of
values
![]() that we can approach in the continuum
limit so that
that we can approach in the continuum
limit so that
![]() in the limit, a behavior which,
as we discussed before in the section in [5], is
typical of second-order phase transitions. Refining a little our analysis
we verify that indeed such a phase transition happens in this model,
related to a process of spontaneous symmetry breaking.
in the limit, a behavior which,
as we discussed before in the section in [5], is
typical of second-order phase transitions. Refining a little our analysis
we verify that indeed such a phase transition happens in this model,
related to a process of spontaneous symmetry breaking.
As we saw, both the distance between the local minima and the width of
each one of the two wells around them are proportional to
![]() , which may be made as large as we wish by
choosing
, which may be made as large as we wish by
choosing ![]() negative and with absolute value much larger than
negative and with absolute value much larger than
![]() . In this way, by adjusting the parameters we can make the two
potential wells much wider than the width of the local distribution,
which is always of the order of
. In this way, by adjusting the parameters we can make the two
potential wells much wider than the width of the local distribution,
which is always of the order of ![]() , thus making it no longer
statistically favorable for the distribution to stay centered around
, thus making it no longer
statistically favorable for the distribution to stay centered around
![]() . The depth of the two wells is given by
. The depth of the two wells is given by
![]() and also increases when we make the absolute
value of
and also increases when we make the absolute
value of ![]() larger than
larger than ![]() , contributing to make it
statistically favorable for the distribution to shift to one of the two
sides, thus falling into one of the two wells. Since the two wells are
identical, this happens in a random way, spontaneously to one of the two
sides, which therefore spontaneously breaks the symmetry which so
far implied that the expectation value of the field had to be zero,
, contributing to make it
statistically favorable for the distribution to shift to one of the two
sides, thus falling into one of the two wells. Since the two wells are
identical, this happens in a random way, spontaneously to one of the two
sides, which therefore spontaneously breaks the symmetry which so
far implied that the expectation value of the field had to be zero,
![]() . Note that the local distribution must fall to
the same side at all sites, otherwise the derivative term would
make a huge unfavorable contribution to the statistical weights. The
situation of broken symmetry is illustrated qualitatively in
figure 1.1.4.
. Note that the local distribution must fall to
the same side at all sites, otherwise the derivative term would
make a huge unfavorable contribution to the statistical weights. The
situation of broken symmetry is illustrated qualitatively in
figure 1.1.4.
We discover in this way that a process of spontaneous symmetry
breaking occurs in this model, giving origin to two phases in the
space of parameters of the model, in each one of which the behavior of
the model is of a certain type, different from the other one. The
expectation value
![]() is the order
parameter of the transition, being equal to zero in one of the phases,
the symmetrical one, and different from zero in the other phase, the
broken-symmetrical one. Since the parameter space is part of a
two-dimensional plane, we expect that the two phases be separated by a
one-dimensional curve. In fact, we can easily estimate the locus of this
phase-transition curve. The argument that leads us to verify that the two
phases exist depends crucially on the width of the potential, which is
proportional to
is the order
parameter of the transition, being equal to zero in one of the phases,
the symmetrical one, and different from zero in the other phase, the
broken-symmetrical one. Since the parameter space is part of a
two-dimensional plane, we expect that the two phases be separated by a
one-dimensional curve. In fact, we can easily estimate the locus of this
phase-transition curve. The argument that leads us to verify that the two
phases exist depends crucially on the width of the potential, which is
proportional to
![]() . This quantity does not change
so long as
. This quantity does not change
so long as ![]() and
and ![]() are proportional to each other,
are proportional to each other,
![]() , so that the location of the points where the
transition occurs, separating the two phases, should depend only on the
proportionality constant
, so that the location of the points where the
transition occurs, separating the two phases, should depend only on the
proportionality constant ![]() .
.
We can estimate this quantity assuming that at the transition the
distance between the two wells is of the order of the width ![]() of the local distribution, whose value is determined predominantly by the
derivative term of the action. It is clear that, if the distance between
the wells is significantly smaller than
of the local distribution, whose value is determined predominantly by the
derivative term of the action. It is clear that, if the distance between
the wells is significantly smaller than ![]() , the local
distribution will tend to remain centered around
, the local
distribution will tend to remain centered around ![]() , with its
width somewhat reduced, while if the distance is significantly larger
than
, with its
width somewhat reduced, while if the distance is significantly larger
than ![]() , the local distribution will tend to shift sideways and
fall into one of the wells. In order to better understand this argument
it is useful to think about the extreme cases, the one in which the total
width of the potential is much smaller than
, the local distribution will tend to shift sideways and
fall into one of the wells. In order to better understand this argument
it is useful to think about the extreme cases, the one in which the total
width of the potential is much smaller than ![]() and the local
distribution is highly squeezed within it, and the one in which the total
width of the potential is much larger than
and the local
distribution is highly squeezed within it, and the one in which the total
width of the potential is much larger than ![]() and the local
distribution is completely free to move within the potential and
therefore to fall into one of the two wells. This estimate gives us the
relation
and the local
distribution is completely free to move within the potential and
therefore to fall into one of the two wells. This estimate gives us the
relation
![]() for the
critical values of the parameters or, more precisely,
for the
critical values of the parameters or, more precisely,
![]() , where
, where ![]() is some
positive constant of the order of
is some
positive constant of the order of ![]() that can only be obtained by a more
complete calculation, and which means that
that can only be obtained by a more
complete calculation, and which means that
![]() . We have therefore an equation
determining the pairs of values
. We have therefore an equation
determining the pairs of values
![]() ,
,
indicating that the locus of the phase transition is a critical line with
a negative slope, which extends from the Gaussian point
![]() all the way to infinity, within the quadrant
all the way to infinity, within the quadrant
![]() in the parameter plane of the model. Of course it
is unlikely that the critical curve is exactly a straight line, because
we did not take into consideration, in this qualitative argument, the
changes in the depth of the wells due to the variation of the parameters,
but we will see later that a straight line is in fact quite a reasonable
approximation. Observe that the symmetrical phase occupies all the
quadrant
in the parameter plane of the model. Of course it
is unlikely that the critical curve is exactly a straight line, because
we did not take into consideration, in this qualitative argument, the
changes in the depth of the wells due to the variation of the parameters,
but we will see later that a straight line is in fact quite a reasonable
approximation. Observe that the symmetrical phase occupies all the
quadrant
![]() and part of the quadrant
and part of the quadrant
![]() , differing therefore from the classical
expectation that making
, differing therefore from the classical
expectation that making ![]() would always break the symmetry. This
is, of course, a direct consequence of the exchange of the classical
point body by an extended quantum object within the potential well.
would always break the symmetry. This
is, of course, a direct consequence of the exchange of the classical
point body by an extended quantum object within the potential well.
We may now draw a critical diagram for the model, illustrating in
this way the two phases and the critical curve, like the one that can be
seen in figure 1.1.5. The half-axis
![]() and the lower half-plane
and the lower half-plane ![]() are not
included in the diagram, of course, since the model is unstable in these
regions. The choice of two functions
are not
included in the diagram, of course, since the model is unstable in these
regions. The choice of two functions ![]() and
and ![]() that
determines a particular continuum limit of the model corresponds to a
path drawn in this diagram, which may start at any point within the
stable region but which must necessarily end at some point of the
critical curve, which is the locus where we have
that
determines a particular continuum limit of the model corresponds to a
path drawn in this diagram, which may start at any point within the
stable region but which must necessarily end at some point of the
critical curve, which is the locus where we have
![]() in the limit. These paths are called flows, or renormalization flows of the model. The Gaussian point is the
critical point of the theory of the free field and the continuum limits
of that model are represented by flows that go along the semi-axis
in the limit. These paths are called flows, or renormalization flows of the model. The Gaussian point is the
critical point of the theory of the free field and the continuum limits
of that model are represented by flows that go along the semi-axis
![]() in the direction of
in the direction of ![]() . We can see here,
once again, that any limits staying within the quadrant
. We can see here,
once again, that any limits staying within the quadrant
![]() must approach the Gaussian point. Flows can approach
the same point of the critical line from either the symmetrical phase or
the broken-symmetrical phase, possibly producing different results.
must approach the Gaussian point. Flows can approach
the same point of the critical line from either the symmetrical phase or
the broken-symmetrical phase, possibly producing different results.
The slope of the critical curve at the Gaussian point is finite and
non-zero and can be calculated by a perturbative approximation, as we
shall see later in this chapter. The slope of the curve at the asymptotic
region is also finite and non-zero, and can be related to critical points
of other models of scalar fields, the so-called non-linear sigma models,
as we shall also see later on. In addition to this, the qualitative
properties of this curve can also be confirmed by means of another
process of approximation that we will examine in detail later on, namely
the so-called mean-field techniques. By and large the nature of the
critical curve is rather well established and understood in any dimension
![]() , and the analysis can be extended without any important
qualitative changes to the models
, and the analysis can be extended without any important
qualitative changes to the models
![]() for
for ![]() , as
well as to multi-component models which are invariant under larger
symmetry groups. In this last case the presence of more field components
does introduce some new elements into the structure, of course. Usually
more precise calculations of the position of the critical lines will
involve some rather intensive and possibly difficult computer work.
, as
well as to multi-component models which are invariant under larger
symmetry groups. In this last case the presence of more field components
does introduce some new elements into the structure, of course. Usually
more precise calculations of the position of the critical lines will
involve some rather intensive and possibly difficult computer work.
Observe that there are many other flows that approach the Gaussian point,
besides those defined directly by the free-field model. For example, we
have a class of flows that go along the vertical half-axis
![]() in the direction of
in the direction of ![]() . This class of
flows can produce trivial limits in which the resulting renormalized mass
is determined by the dimensionless coupling parameter
. This class of
flows can produce trivial limits in which the resulting renormalized mass
is determined by the dimensionless coupling parameter ![]() , instead
of by
, instead
of by ![]() . This phenomenon, which we can see here in a very simple
way, is also known by the name of ``dimensional transmutation''. It is
also possible to approach the Gaussian point from the broken-symmetrical
phase, from under the critical curve. In this way we may define trivial
limits in which the field, although free, has non-zero expectation values
. This phenomenon, which we can see here in a very simple
way, is also known by the name of ``dimensional transmutation''. It is
also possible to approach the Gaussian point from the broken-symmetrical
phase, from under the critical curve. In this way we may define trivial
limits in which the field, although free, has non-zero expectation values
![]() . Except in the case
. Except in the case ![]() any limits that are
candidates to not being trivial must approach some other point of the
critical curve, and not the Gaussian point. If all possible flows of the
model turn out to be trivial then we say that the model is trivial. Then,
except for the introduction of the concept of spontaneous symmetry
breaking, such models are just another way to produce the theory of the
free scalar field in the continuum limit. They may still be useful test
models on finite lattices, though.
any limits that are
candidates to not being trivial must approach some other point of the
critical curve, and not the Gaussian point. If all possible flows of the
model turn out to be trivial then we say that the model is trivial. Then,
except for the introduction of the concept of spontaneous symmetry
breaking, such models are just another way to produce the theory of the
free scalar field in the continuum limit. They may still be useful test
models on finite lattices, though.
Observe that what we have obtained here is a type of critical behavior
just like the one described in the section
in [5], where the quantity
![]() plays the role played by the magnetization
in the case of statistical mechanics, as shown in the first figure of
that section. However, we can do a little better here, and continue our
heuristic argument in order to get an estimate for
plays the role played by the magnetization
in the case of statistical mechanics, as shown in the first figure of
that section. However, we can do a little better here, and continue our
heuristic argument in order to get an estimate for ![]() as a function
of
as a function
of ![]() and
and ![]() . First of all let us point out that we should
be able to get only the absolute value of
. First of all let us point out that we should
be able to get only the absolute value of ![]() and not its sign, since
the symmetry can break to either side. Let us therefore estimate
and not its sign, since
the symmetry can break to either side. Let us therefore estimate
![]() and not
and not ![]() . It must be zero at the critical line, that
is, when the squared width of the potential,
. It must be zero at the critical line, that
is, when the squared width of the potential,
![]() , is equal
to the squared width of the local distribution,
, is equal
to the squared width of the local distribution,
![]() . It must also be equal to zero whenever the
potential is less wide than that, that is,
. It must also be equal to zero whenever the
potential is less wide than that, that is,
characterizing the symmetrical phase. To this we may add that, if the
potential is wider than the width of the local distribution, then the
distribution should be able to shift to one side by something like the
difference between the two, giving as the corresponding estimate for
![]() the value
the value
characterizing the broken-symmetrical phase. Note that this formula gives
the correct value ![]() at the critical line. It also gives the
correct value in the case of an extremely wide potential, in which case
at the critical line. It also gives the
correct value in the case of an extremely wide potential, in which case
![]() , which is always of the order of
, which is always of the order of ![]() , can be
neglected by comparison with
, can be
neglected by comparison with
![]() , and we should have the
average
, and we should have the
average ![]() of the local distribution sitting at the minimum of the
potential, that is,
of the local distribution sitting at the minimum of the
potential, that is,
![]() . In short, we have for
. In short, we have for
![]() the result
the result
whenever the quantity in parenthesis is negative, and zero otherwise.
Note that the quantity in parenthesis coincides with the equation of the
critical line, thus showing that indeed ![]() is zero over that
line. Note also that the result for
is zero over that
line. Note also that the result for ![]() contains
contains ![]() ,
possibly indicating that a calculation which is purely perturbative in
,
possibly indicating that a calculation which is purely perturbative in
![]() may not be sufficient to obtain this result.
may not be sufficient to obtain this result.
We may also obtain estimates for the dimensionless squared mass
![]() , using arguments similar to the ones above. Starting with
the symmetrical phase, which contains the possibility that
, using arguments similar to the ones above. Starting with
the symmetrical phase, which contains the possibility that ![]() ,
with
,
with ![]() , we know two things about
, we know two things about ![]() : first, it must be
zero over the critical line, and second it must be equal to
: first, it must be
zero over the critical line, and second it must be equal to ![]() when
when
![]() . Since the equation of the critical line contains a term
linear in
. Since the equation of the critical line contains a term
linear in ![]() , it is clear that in order to satisfy both these
criteria we must make
, it is clear that in order to satisfy both these
criteria we must make ![]() equal to that equation, thus obtaining
equal to that equation, thus obtaining
where the condition is the same as before, characterizing the symmetrical
phase. In the broken-symmetrical phase we must work a little more to get
the result. First of all, let us discuss why there should be a non-zero
physical mass in this case. This is so because, after the symmetry breaks
and the local distribution falls within one of the two wells, it will
become squeezed by it, leading to an increase in the renormalized mass,
is a way similar to what happens in the free theory. So it follows that
![]() should have its minimum of zero at the critical line and
increase when one goes away from it on either side.
should have its minimum of zero at the critical line and
increase when one goes away from it on either side.
In order to estimate the value that ![]() should have in the
broken-symmetrical phase, let us go deeply into it, making
should have in the
broken-symmetrical phase, let us go deeply into it, making
![]() , so that the potential is very wide and the local
distribution is sitting around one of the two local minima. Under these
conditions we may approximate the potential in the relatively small
region where the local distribution is significantly different from zero
by a parabola. If we calculate the second derivative of the potential at
the minimum, which gives the curvature of this parabola, we get for it
the value
, so that the potential is very wide and the local
distribution is sitting around one of the two local minima. Under these
conditions we may approximate the potential in the relatively small
region where the local distribution is significantly different from zero
by a parabola. If we calculate the second derivative of the potential at
the minimum, which gives the curvature of this parabola, we get for it
the value ![]() , which is positive because
, which is positive because ![]() is negative. By
comparison with the situation in free theory we see now that deep in the
broken-symmetrical phase we should have
is negative. By
comparison with the situation in free theory we see now that deep in the
broken-symmetrical phase we should have
![]() . Adding to
this that in this phase
. Adding to
this that in this phase ![]() still must be zero over the critical
line, we see that we must make
still must be zero over the critical
line, we see that we must make ![]() proportional to the equation
of the line, with a constant of proportionality that will bring about the
correct value in the deeply broken regime. With all this it is not
difficult to see that we must have
proportional to the equation
of the line, with a constant of proportionality that will bring about the
correct value in the deeply broken regime. With all this it is not
difficult to see that we must have
where the condition is once again the same as before, characterizing the
broken-symmetrical phase. Note that the value ![]() for the
curvature of the parabola near the minimum only goes to zero is we make
for the
curvature of the parabola near the minimum only goes to zero is we make
![]() and hence go back to the Gaussian point. Therefore the
potential never becomes infinitely flat around its local minima in the
broken-symmetrical phase, except in limits that approach the Gaussian
point. There are, therefore, no other possible continuum limits with
finite masses in this phase, except those that tend to the Gaussian point
or to some other point of the critical line.
and hence go back to the Gaussian point. Therefore the
potential never becomes infinitely flat around its local minima in the
broken-symmetrical phase, except in limits that approach the Gaussian
point. There are, therefore, no other possible continuum limits with
finite masses in this phase, except those that tend to the Gaussian point
or to some other point of the critical line.
As a last refining touch of our argument, we may point out its relation
to the question of the triviality of the model. Let us look back at
figure 1.1.3 and imagine that it represents
the critical situation, in which the potential is just wide enough not to
squeeze the local distribution. This means that the local distribution is
almost free to move, but there is no space for it to actually do so. In
this situation the squeezing action of the outer walls of the potential
and the spreading action of the central bump are exactly balanced, so
that the net action over the width of the local distribution vanishes.
However, even without changing the width, the potential can tend to
change the shape of the distribution. In fact, if we consider in
which parts of the local distribution the central bump and the outer
walls act, we realize that the bump tends to flatten and spread the top
of the Gaussian, while the two outer walls tend to increase the slopes on
the two sides of the distribution. This change of shape is exactly what
one would expect if the local distribution tended to be more like the
function
![]() than like a Gaussian.
than like a Gaussian.
In fact, one would expect ![]() to manifest itself by affecting
the form of the complete local distribution. Since
to manifest itself by affecting
the form of the complete local distribution. Since ![]() is
related to the second moment of the distribution, its width, it is
reasonable to expect that
is
related to the second moment of the distribution, its width, it is
reasonable to expect that ![]() is correspondingly related to the
fourth moment of the distribution, and hence to the shape of the curve
that describes it. However, our experience with
is correspondingly related to the
fourth moment of the distribution, and hence to the shape of the curve
that describes it. However, our experience with ![]() shows that,
due to the derivative term of the action, the local distribution has a
very rigid character in the continuum limit, as a consequence of the
requirements of propagation, which requires
shows that,
due to the derivative term of the action, the local distribution has a
very rigid character in the continuum limit, as a consequence of the
requirements of propagation, which requires ![]() to go to zero in
the limit. There is therefore legitimate doubt that we can have this
distribution significantly changed in shape in the continuum limit, to
allow for a non-zero value of
to go to zero in
the limit. There is therefore legitimate doubt that we can have this
distribution significantly changed in shape in the continuum limit, to
allow for a non-zero value of ![]() , without disturbing the
dynamics of propagation and thus ending up with infinitely massive
particles and no propagation. Note that if it is true that we must have
, without disturbing the
dynamics of propagation and thus ending up with infinitely massive
particles and no propagation. Note that if it is true that we must have
![]() in the limit, then it is imperative that
in the limit, then it is imperative that
![]() be zero exactly over the critical line, where we already
know that
be zero exactly over the critical line, where we already
know that ![]() is zero, otherwise there would be no possible
continuum limits except those going to the Gaussian point.
is zero, otherwise there would be no possible
continuum limits except those going to the Gaussian point.
Of course we cannot resolve this difficult matter with only heuristic
arguments. In fact, we will see that perturbation theory is also not
enough to handle this issue, and we will have to use computer simulations
in order to explore it. However, we can say that, if indeed it turns out
that we must have
![]() in the limit, then only
theories that can be non-trivial with
in the limit, then only
theories that can be non-trivial with ![]() going to zero still
have a chance of being truly interacting quantum theories. This involves
the scaling relations between
going to zero still
have a chance of being truly interacting quantum theories. This involves
the scaling relations between ![]() and its dimensionfull version
and its dimensionfull version
![]() . As is discussed in problem 1.1.8, in
the classical case, this leaves, of all polynomial models
. As is discussed in problem 1.1.8, in
the classical case, this leaves, of all polynomial models ![]() ,
,
![]() , in all dimensions
, in all dimensions
![]() , a single
possibility: the
, a single
possibility: the
![]() model in
model in ![]() .
.
We end this section with a short discussion of the continuum limit of the
classical theory, which requires rewriting the action of the model in
terms of dimensionfull quantities. If we recall our discussion about the
physical significance of the block variables in the section
in [6], we will see that it is the dimensionfull variables and parameters that have a more direct physical
relevance in the quantum theory. While the dimensionless local variables
and parameters, usually numbers of the order of ![]() that do not scale
significantly in the continuum limit, are convenient both for
establishing mathematical facts about the internal structure of the
models and for dealing with them in a practical way in computer
simulations, the dimensionfull variables include scale factors that cause
them to scale in the continuum limit in the correct way in order to
represent the superpositions of the dimensionless observables over the
large and increasing numbers of sites contained within the blocks. As we
discussed in that section, such superpositions constitute the only type
of quantity within the theory that can in fact be directly observed.
that do not scale
significantly in the continuum limit, are convenient both for
establishing mathematical facts about the internal structure of the
models and for dealing with them in a practical way in computer
simulations, the dimensionfull variables include scale factors that cause
them to scale in the continuum limit in the correct way in order to
represent the superpositions of the dimensionless observables over the
large and increasing numbers of sites contained within the blocks. As we
discussed in that section, such superpositions constitute the only type
of quantity within the theory that can in fact be directly observed.
The definition of the dimensionfull field in terms of the dimensionless
field in the
![]() model is the same as in the theory of
the free field,
model is the same as in the theory of
the free field,
![]() , since it is determined only by
the derivative term. We do not have in this case a mass term properly
speaking, since
, since it is determined only by
the derivative term. We do not have in this case a mass term properly
speaking, since ![]() can be both positive and negative, but in a way
similar to that of the theory of the free field we may introduce a
parameter
can be both positive and negative, but in a way
similar to that of the theory of the free field we may introduce a
parameter ![]() with dimensions of mass by means of the relation
with dimensions of mass by means of the relation
![]() . A simple analysis of the quartic term gives us,
finally, the definition of the dimensionfull coupling constant
. A simple analysis of the quartic term gives us,
finally, the definition of the dimensionfull coupling constant
![]() . The treatment of the sums over links and sites
and of the finite differences in the continuum limit of the classical
theory, in terms of integrals and derivatives, is identical to the one
discussed in the case of the free theory, so that we obtain for the
action
. The treatment of the sums over links and sites
and of the finite differences in the continuum limit of the classical
theory, in terms of integrals and derivatives, is identical to the one
discussed in the case of the free theory, so that we obtain for the
action ![]() in the continuum limit, in terms of the dimensionfull
quantities,
in the continuum limit, in terms of the dimensionfull
quantities,
![\begin{displaymath}
S[\phi]=\int_{V}{\rm d}^{d}x\left\{
\frac{1}{2}\sum_{\mu}\le...
...\phi^{2}(\vec{x})+\frac{\Lambda}{4}\phi^{4}(\vec{x})
\right\},
\end{displaymath}](img120.gif)
where the sign of the quadratic term depends on the sign of ![]() .
Observe that the relation existing between the parameters
.
Observe that the relation existing between the parameters ![]() and
and
![]() of the classical theory implies that, since
of the classical theory implies that, since ![]() must
remain finite in the limit,
must
remain finite in the limit, ![]() must behave in different and
definite ways in each space-time dimension. For
must behave in different and
definite ways in each space-time dimension. For ![]() it is necessary
that
it is necessary
that ![]() diverge to infinity in the limit in order that
diverge to infinity in the limit in order that ![]() be different from zero, which shows that these classical theories have a
rather singular behavior in this case. For
be different from zero, which shows that these classical theories have a
rather singular behavior in this case. For ![]() , on the other hand,
it is necessary that
, on the other hand,
it is necessary that
![]() in the limit in order for
in the limit in order for
![]() to remain finite, showing that in this case the behavior is the
reverse of that of the previous case. For
to remain finite, showing that in this case the behavior is the
reverse of that of the previous case. For ![]() we have that
we have that
![]() and therefore in this case it is not possible to make
any definite statement of this type. Given these scaling relations
between
and therefore in this case it is not possible to make
any definite statement of this type. Given these scaling relations
between ![]() and
and ![]() it is reasonable to think that the
dimensionfull renormalized coupling constant
it is reasonable to think that the
dimensionfull renormalized coupling constant ![]() should be
defined in terms of
should be
defined in terms of ![]() in an analogous way.
in an analogous way.
Our expectation is that, just as it is the constant ![]() that has
physical relevance in the classical theory, the constant
that has
physical relevance in the classical theory, the constant ![]() should play the same role in the quantum theory. As was already pointed
out, the analysis of the block propagator of the free theory in the
section in [6] indicated that it is the
dimensionfull quantities, based on the dimensionfull field
should play the same role in the quantum theory. As was already pointed
out, the analysis of the block propagator of the free theory in the
section in [6] indicated that it is the
dimensionfull quantities, based on the dimensionfull field ![]() , that
have direct physical relevance, being directly related to the quantities
which are observable in the quantum theory. Although we have only shown
this fact in the case of the free theory, we will assume that it is true
in general, a working hypothesis that we will only be able to confirm a
posteriori by the accumulation of calculational experience, numerical or
otherwise. We will see that this relation of scale between
, that
have direct physical relevance, being directly related to the quantities
which are observable in the quantum theory. Although we have only shown
this fact in the case of the free theory, we will assume that it is true
in general, a working hypothesis that we will only be able to confirm a
posteriori by the accumulation of calculational experience, numerical or
otherwise. We will see that this relation of scale between ![]() and
and ![]() will be very useful to enable us to understand
heuristically the behavior of the quantum models. Before anything else is
done, however, it will be necessary to define in a more precise way the
constant
will be very useful to enable us to understand
heuristically the behavior of the quantum models. Before anything else is
done, however, it will be necessary to define in a more precise way the
constant ![]() of the quantum theory, which we will do in the
third chapter of this book.
of the quantum theory, which we will do in the
third chapter of this book.
![\begin{displaymath}
S[\varphi]=\frac{1}{2}\sum_{\ell}(\Delta_{\ell}\varphi)^{2}
...
..._{s}\varphi^{2}(s)
+\frac{\lambda}{2p}\sum_{s}\varphi^{2p}(s),
\end{displaymath}](img127.gif)
verifying that the spontaneous symmetry breaking situation is
qualitatively similar to that of the
![]() model. Sketch
qualitatively the phase diagrams of these models and estimate whether the
critical curves in these cases are more or less steep than the critical
curve of the quartic model.
model. Sketch
qualitatively the phase diagrams of these models and estimate whether the
critical curves in these cases are more or less steep than the critical
curve of the quartic model.