Next: Interactions Between Particles Up: The Sigma-Model Limit Previous: The Mean Field Method Contents
We will perform in this section a few analytical calculations, in the
usual mean-field approximation with ![]() , of some observables of the
scalar field models, using the ideas presented in section 2.2.
The approximations with
, of some observables of the
scalar field models, using the ideas presented in section 2.2.
The approximations with ![]() , involving the extension of the method
which was also discussed in that section, are usually too complex for an
analytical treatment and are better characterized, therefore, as material
for performing stochastic simulations, which will be discussed in a
future volume. The calculations we will present here can be understood as
exact analytical solutions for the lattice systems with a single active
site. We will start with the Ising models, in which the calculations are
somewhat simpler.
, involving the extension of the method
which was also discussed in that section, are usually too complex for an
analytical treatment and are better characterized, therefore, as material
for performing stochastic simulations, which will be discussed in a
future volume. The calculations we will present here can be understood as
exact analytical solutions for the lattice systems with a single active
site. We will start with the Ising models, in which the calculations are
somewhat simpler.
A quantity of particular interest in the Ising models is the
magnetization, which is the order parameter of these models. It can be
defined as the expectation value ![]() of the field, which will be
pointing predominantly in the direction that we choose arbitrarily for
the symmetry breaking. This is the direction in which we will keep
oriented the fields at the border. We will calculate
of the field, which will be
pointing predominantly in the direction that we choose arbitrarily for
the symmetry breaking. This is the direction in which we will keep
oriented the fields at the border. We will calculate ![]() in the
mean-field approximation as a function of the parameter
in the
mean-field approximation as a function of the parameter ![]() and of
the dimension
and of
the dimension ![]() of space-time. As we saw before in
section 2.2, the parameter
of space-time. As we saw before in
section 2.2, the parameter ![]() can be understood as the
inverse of a fictitious temperature. For a given value of
can be understood as the
inverse of a fictitious temperature. For a given value of ![]() , the
critical point
, the
critical point ![]() is the value of the inverse temperature for
which the magnetization
is the value of the inverse temperature for
which the magnetization
![]() ceases to be zero, when we
``cool'' the system and therefore increase
ceases to be zero, when we
``cool'' the system and therefore increase ![]() . For the calculations
it is convenient to use the dimensionless field
. For the calculations
it is convenient to use the dimensionless field ![]() that was
introduced in section 2.2, so that for the purposes of this
section we will use, rather than
that was
introduced in section 2.2, so that for the purposes of this
section we will use, rather than
![]() , the
quantity
, the
quantity
![]() , where
, where
![]() .
It is
.
It is ![]() rather than
rather than ![]() that is more closely related to the
standard definition of the magnetization of statistical mechanics. As was
derived in that section, the action can be written in terms of
that is more closely related to the
standard definition of the magnetization of statistical mechanics. As was
derived in that section, the action can be written in terms of ![]() as
as
![\begin{displaymath}
S[\psi]=-\beta\sum_{\ell}\psi(\ell_{-})\psi(\ell_{+}),
\end{displaymath}](img440.gif)
while the constraint is written as
where the field ![]() is, therefore, either
is, therefore, either ![]() or
or ![]() . We now freeze
all the sites except one at the value
. We now freeze
all the sites except one at the value ![]() , arbitrarily
choosing the positive direction as the direction of orientation of the
fields. Therefore in our
, arbitrarily
choosing the positive direction as the direction of orientation of the
fields. Therefore in our ![]() mean-field approximation the relation
mean-field approximation the relation
![]() can be written as
can be written as
![\begin{displaymath}
\nu_{R}=\frac{\displaystyle \sum[\psi=\pm 1]\;\psi\;e^{2d \...
...i}}{\displaystyle \sum[\psi=\pm 1]\;e^{2d \beta\nu_{R}\psi}}.
\end{displaymath}](img445.gif)
Since the sum is over a single site, in this simple ![]() case we can
immediately write the result as
case we can
immediately write the result as
thus obtaining an algebraic equation that in principle gives us the
complete solution for ![]() in the
in the ![]() system. This equation can be
solved numerically in order to provide us with graphs of
system. This equation can be
solved numerically in order to provide us with graphs of ![]() as a
function of
as a
function of ![]() (problem 2.3.2). It can also
be used to determine the value of
(problem 2.3.2). It can also
be used to determine the value of ![]() at which
at which ![]() becomes
the only possible solution (problem 2.3.1), by the
use of series expansions. However, the simplest way to obtain the
critical points is to simply expand its right-hand side around
becomes
the only possible solution (problem 2.3.1), by the
use of series expansions. However, the simplest way to obtain the
critical points is to simply expand its right-hand side around
![]() . This is sufficient to determine the critical points because
the phase transition is of second order in these models and, therefore,
we have that
. This is sufficient to determine the critical points because
the phase transition is of second order in these models and, therefore,
we have that
![]() for
for
![]() . Expanding
and keeping only up to first-order terms
(problem 2.3.3) we get
. Expanding
and keeping only up to first-order terms
(problem 2.3.3) we get
A factor of ![]() cancels off and we are left with
cancels off and we are left with
After the cancellation of the trivial solution ![]() we may impose
the condition
we may impose
the condition ![]() in order to find the region where only this zero solution is possible. Observe that the equation above
does not depend on
in order to find the region where only this zero solution is possible. Observe that the equation above
does not depend on ![]() . Had we kept the higher-order terms of the
expansion, the condition
. Had we kept the higher-order terms of the
expansion, the condition ![]() would eliminate them at this point,
leaving only the equation above. Hence we obtain the mean-field
approximation for the critical points
would eliminate them at this point,
leaving only the equation above. Hence we obtain the mean-field
approximation for the critical points
This technique of expansion around the critical point is useful in cases in which the mean-field results cannot be obtained explicitly, or in which the exact solutions of the resulting equations are difficult to determine analytically.
In four dimensions this ![]() result is in fairly good agreement with the
numerical results obtained for larger values of
result is in fairly good agreement with the
numerical results obtained for larger values of ![]() . The agreement is
poorer in three dimensions, very poor is two dimensions, and the result
fails completely in one dimension, in which there is no critical point at
all. Observe that the success or lack thereof on the
. The agreement is
poorer in three dimensions, very poor is two dimensions, and the result
fails completely in one dimension, in which there is no critical point at
all. Observe that the success or lack thereof on the ![]() approximation
in reproducing well the results for large values of
approximation
in reproducing well the results for large values of ![]() is not a
diagnostic about the validity of the method itself, bur rather an
indication of whether or not the results for increasing values of
is not a
diagnostic about the validity of the method itself, bur rather an
indication of whether or not the results for increasing values of ![]() accumulate around some finite value of
accumulate around some finite value of ![]() . For
. For ![]() the values
the values
![]() for each lattice size diverge to
for each lattice size diverge to ![]() when
when
![]() , so that no finite lattice can represent well the
limit. In larger dimensions the critical points
, so that no finite lattice can represent well the
limit. In larger dimensions the critical points ![]() of the
finite lattices converge to finite values in the
of the
finite lattices converge to finite values in the
![]() limit, so that in these cases the approximation of the limiting result by
the results for finite lattices makes some sense, being better or worse
depending on the speed of convergence.
limit, so that in these cases the approximation of the limiting result by
the results for finite lattices makes some sense, being better or worse
depending on the speed of convergence.
Table 2.3.1 contains results for the critical points of
the Ising models for dimensions from ![]() up to
up to ![]() . For
. For ![]() the
result was obtained by means of extrapolations to the
the
result was obtained by means of extrapolations to the
![]() limit of the results of stochastic simulations with
periodical boundary conditions on lattices with
limit of the results of stochastic simulations with
periodical boundary conditions on lattices with ![]() from
from ![]() to
to ![]() . For
. For
![]() we quote the most precise result that we know
about [36]. For
we quote the most precise result that we know
about [36]. For ![]() we quote the well-known result
for the two-dimensional Ising model [37]. Since the
estimate from periodical simulations is obtained from the continuous and
differentiable curves of the magnetization as a function of
we quote the well-known result
for the two-dimensional Ising model [37]. Since the
estimate from periodical simulations is obtained from the continuous and
differentiable curves of the magnetization as a function of ![]() , the
error bars indicated are only approximate estimates. The entry
, the
error bars indicated are only approximate estimates. The entry ![]() indicates the case in which the theorems about long-distance
order [31] imply that there is no phase
transition, which is the same in which
indicates the case in which the theorems about long-distance
order [31] imply that there is no phase
transition, which is the same in which
![]() when
when
![]() in the simulations with self-consistent fixed
boundary conditions. The results of equation (2.3.2)
are also included, for comparison. As one can see, in
in the simulations with self-consistent fixed
boundary conditions. The results of equation (2.3.2)
are also included, for comparison. As one can see, in ![]() the
mean-field result deviates about 17% from the numerical results, while
for
the
mean-field result deviates about 17% from the numerical results, while
for ![]() it deviates by about 25%.
it deviates by about 25%.
Calculating the magnetization in an infinitesimal neighborhood of
![]() one can also obtain the mean-field approximation for the
corresponding critical exponent. The definition of this critical exponent
is as follows. If we have, close to the critical point in the
broken-symmetrical phase,
one can also obtain the mean-field approximation for the
corresponding critical exponent. The definition of this critical exponent
is as follows. If we have, close to the critical point in the
broken-symmetrical phase,
for some non-vanishing constant ![]() , then
, then ![]() is the critical
exponent of
is the critical
exponent of ![]() . Once more, this can be done using the complete
solution in terms of the hyperbolic functions
(problem 2.3.4), but the simplest way to
obtain the result is to expand equation (2.3.1) to
third order in
. Once more, this can be done using the complete
solution in terms of the hyperbolic functions
(problem 2.3.4), but the simplest way to
obtain the result is to expand equation (2.3.1) to
third order in ![]() (problem 2.3.3), thus
obtaining
(problem 2.3.3), thus
obtaining
Once more a factor of ![]() cancels out and we obtain
cancels out and we obtain
![\begin{displaymath}
1=2d \beta\left[1-\frac{4}{3}d^{2}\beta^{2}\nu_{R}^{2}\right].
\end{displaymath}](img467.gif)
Remembering that
![]() and considering that we are in the
vicinity of the critical point, with
and considering that we are in the
vicinity of the critical point, with
![]() , we may
write this as
, we may
write this as
This shows that the mean-field approximation for the critical exponent is
![]() , and determines the value of the constant
, and determines the value of the constant
![]() . This value for the critical exponent of the
magnetization is characteristic of the mean-field calculations with
. This value for the critical exponent of the
magnetization is characteristic of the mean-field calculations with
![]() .
.
Another mean-field calculation of interest is that of the critical curves
of the
![]() polynomial models, which are given by
equation of the type
polynomial models, which are given by
equation of the type
![]() . In this case we will use the
usual dimensionless field
. In this case we will use the
usual dimensionless field ![]() as our variable. If we define the
magnetization for this case as
as our variable. If we define the
magnetization for this case as
![]() we may
write, in the
we may
write, in the ![]() mean-field approximation,
mean-field approximation,
![\begin{displaymath}
v_{R}=\frac{\displaystyle \int_{-\infty}^{\infty}{\rm d}\var...
...\left[(d+\alpha/2)\varphi^{2}+(\lambda/4)\varphi^{4}\right]}}.
\end{displaymath}](img473.gif)
If we use here our ``radial-angular'' decomposition of ![]() into its
absolute value and its sign,
into its
absolute value and its sign,
![]() , with
, with ![]() ,
as was done in section 2.1, we may write this as
,
as was done in section 2.1, we may write this as
![\begin{displaymath}
v_{R}=\frac{\displaystyle \sum[\psi=\pm 1]\int_{0}^{\infty}{...
...\left[(d+\alpha/2)\varphi^{2}+(\lambda/4)\varphi^{4}\right]}}.
\end{displaymath}](img475.gif)
We may now execute the sum over the single active site and hence get
In this case it is also possible to perform the integrations analytically
in terms of special functions (problem 2.3.5) but,
close to the critical curve, it suffices to calculate the right-hand side
of this equation for small values of ![]() . Therefore, we expand
equation (2.3.5) to first order in
. Therefore, we expand
equation (2.3.5) to first order in ![]() and
obtain
and
obtain
![\begin{displaymath}
v_{R}=2d v_{R}\;\frac{\displaystyle \int_{0}^{\infty}{\rm d...
...\left[(d+\alpha/2)\varphi^{2}+(\lambda/4)\varphi^{4}\right]}}.
\end{displaymath}](img477.gif)
Just like before, a factor of ![]() cancels out and we obtain as our
mean-field result an equation giving implicitly the critical curve
cancels out and we obtain as our
mean-field result an equation giving implicitly the critical curve
![]() ,
,
Once more the integrations can be done, this time in terms of the
parabolic cylinder functions ![]() (problem 2.3.6), but this does not help us to solve
this equation in order to write the equation of the critical curve in
explicit form. The fact that the left-hand side of this equation is equal
to the mean-field value of the critical point
(problem 2.3.6), but this does not help us to solve
this equation in order to write the equation of the critical curve in
explicit form. The fact that the left-hand side of this equation is equal
to the mean-field value of the critical point ![]() of the
corresponding Ising model is not an accident, it is clearly related to
the fact that the
of the
corresponding Ising model is not an accident, it is clearly related to
the fact that the
![]() limits of the
limits of the
![]() models converge to the Ising models
(problem 2.3.7).
models converge to the Ising models
(problem 2.3.7).
Although we are not able to solve equation (2.3.6)
analytically in order to write the equation
![]() of the
critical curve in explicit form, it is possible to solve the asymptotic
form of the equation, for large values of
of the
critical curve in explicit form, it is possible to solve the asymptotic
form of the equation, for large values of ![]() (problem 2.3.8). Doing this we discover that in this
limit the critical curve is asymptotic to the straight line defined by
the equation
(problem 2.3.8). Doing this we discover that in this
limit the critical curve is asymptotic to the straight line defined by
the equation
where
![]() are the critical points of the corresponding
Ising models, so that the asymptote cuts the
are the critical points of the corresponding
Ising models, so that the asymptote cuts the ![]() axis at the point
axis at the point
![]() and forms with the negative
and forms with the negative ![]() semi-axis an angle
semi-axis an angle
![]() such that
such that
![]() . Expanding
equation (2.3.6) for small values of
. Expanding
equation (2.3.6) for small values of ![]() and
and
![]() one can also obtain the slope of the tangent line to the
critical curve at the Gaussian point (problem 2.3.9).
Doing this we obtain for this tangent line the equation
one can also obtain the slope of the tangent line to the
critical curve at the Gaussian point (problem 2.3.9).
Doing this we obtain for this tangent line the equation
We see that the asymptotic slope is ![]() , larger therefore than
the slope at the Gaussian point, which is
, larger therefore than
the slope at the Gaussian point, which is
![]() , by a factor
of
, by a factor
of ![]() , thus showing that the critical curve has its concavity turned
mostly upwards.
, thus showing that the critical curve has its concavity turned
mostly upwards.
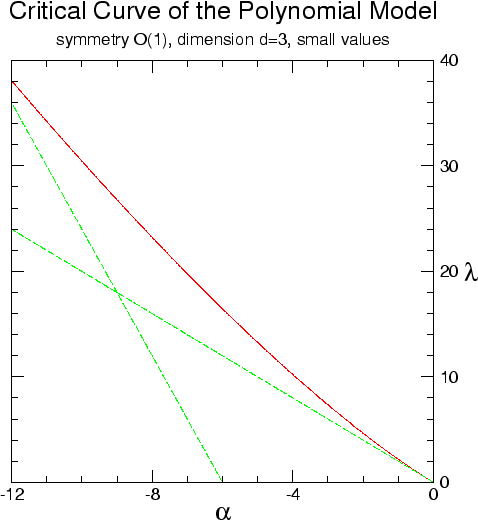 |
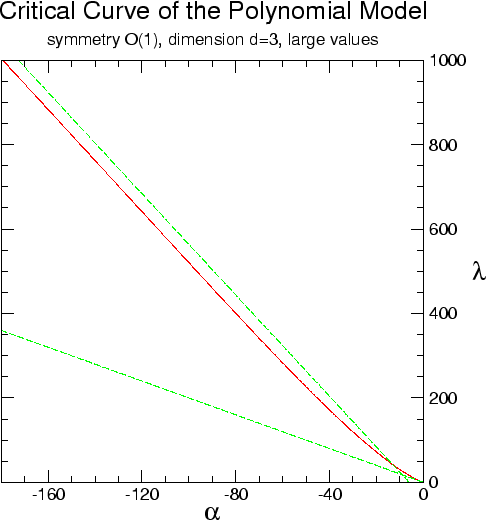 |
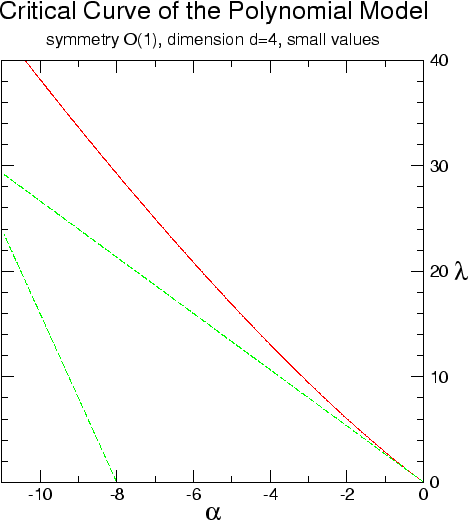 |
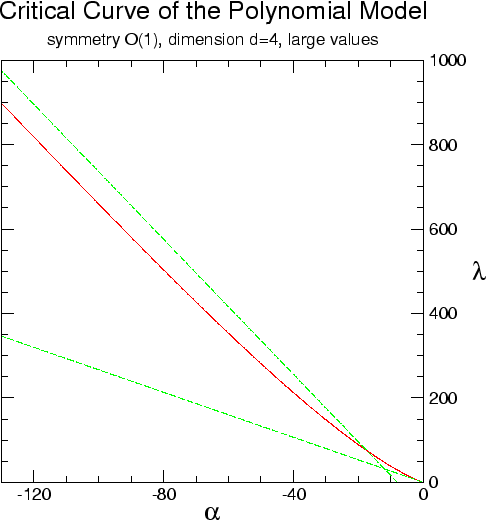 |
In order to get the graphs of the critical curve we are compelled to
solve the equation by numerical means. In fact, this can be done not only
for our ![]() case here, but for the
case here, but for the
![]() generalizations as well. A
curious fact is that it is in fact easier to do this for
generalizations as well. A
curious fact is that it is in fact easier to do this for
![]() and the
other even-
and the
other even-![]() cases than for
cases than for
![]() and the other odd-
and the other odd-![]() cases,
because in the even-
cases,
because in the even-![]() cases it turns out that the integrals can be
written in terms of the error function. For the odd-
cases it turns out that the integrals can be
written in terms of the error function. For the odd-![]() cases we must
use direct numerical integration in order to solve the equation, which is
a technique that can be used in all cases [38].
The graphs in figures from 2.3.1
to 2.3.4 show the critical curves
obtained by such numerical means in a few cases. Each graph shows also
the tangent line at the Gaussian point and the asymptotic line for large
values of
cases we must
use direct numerical integration in order to solve the equation, which is
a technique that can be used in all cases [38].
The graphs in figures from 2.3.1
to 2.3.4 show the critical curves
obtained by such numerical means in a few cases. Each graph shows also
the tangent line at the Gaussian point and the asymptotic line for large
values of ![]() .
.
Figure 2.3.1 shows the solution in the
case ![]() , for fairly small values of the parameters
, for fairly small values of the parameters ![]() and
and
![]() , while figure 2.3.2 shows the
same solution for larger values of the parameters.
Figures 2.3.3
and 2.3.4 show the corresponding data
for the case
, while figure 2.3.2 shows the
same solution for larger values of the parameters.
Figures 2.3.3
and 2.3.4 show the corresponding data
for the case ![]() . It should be noted that, as one can see in the two
graphs with the larger values of the parameters, the asymptotic lines
actually cross the critical curves. This implies that at some location
for even larger values of the parameters the critical curves must have
inflection points and reverse their concavities, presumably approaching
their asymptotes from below rather than from above. One can see, looking
directly at the data shown in the graphs, that the critical curves do in
fact slowly approach the asymptotes, but it seems that the location of
the inflection point is at very large values of the parameters, that so
far have not been probed numerically. It is interesting to observe that
this behavior seems to be characteristic of the
. It should be noted that, as one can see in the two
graphs with the larger values of the parameters, the asymptotic lines
actually cross the critical curves. This implies that at some location
for even larger values of the parameters the critical curves must have
inflection points and reverse their concavities, presumably approaching
their asymptotes from below rather than from above. One can see, looking
directly at the data shown in the graphs, that the critical curves do in
fact slowly approach the asymptotes, but it seems that the location of
the inflection point is at very large values of the parameters, that so
far have not been probed numerically. It is interesting to observe that
this behavior seems to be characteristic of the ![]() models. In the
models. In the
![]() models with
models with
![]() one does not see this type of crossing, and
the critical curves seem to approach their asymptotes from above.
one does not see this type of crossing, and
the critical curves seem to approach their asymptotes from above.
We are led to conclude that the mean-field approximation confirms the
basic properties of the critical curves that we discussed before in
sections 1.1 and 1.3. One can improve on the comparison
with the perturbative results by calculating the mean-field approximation
for the quantity
![]() over the critical
curve, where
over the critical
curve, where
![]() is zero. The mean-field
approximation for
is zero. The mean-field
approximation for ![]() is given by
is given by
![\begin{displaymath}
\sigma_{\rm MF}^{2}=\frac{\displaystyle \sum[\psi=\pm 1]\int...
...\left[(d+\alpha/2)\varphi^{2}+(\lambda/4)\varphi^{4}\right]}},
\end{displaymath}](img492.gif)
and if we execute the sum over the signs at the single active site we get
![\begin{displaymath}
\sigma_{\rm MF}^{2}=\frac{\displaystyle \int_{0}^{\infty}{\r...
...\left[(d+\alpha/2)\varphi^{2}+(\lambda/4)\varphi^{4}\right]}}.
\end{displaymath}](img493.gif)
At the critical curve, where ![]() , this reduces to
, this reduces to
![\begin{displaymath}
\sigma_{\rm MF}^{2}=\frac{\displaystyle \int_{0}^{\infty}{\r...
...\left[(d+\alpha/2)\varphi^{2}+(\lambda/4)\varphi^{4}\right]}}.
\end{displaymath}](img493.gif)
Note that the right-hand side of this equation is exactly equal to the right-hand side of equation (2.3.6), which determines the critical line, and that therefore we have
so that the equation of the tangent line to the mean-field critical curve at the Gaussian point can be written as
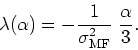
If we now recall the perturbative result for the equation of the tangent line to the critical curve at the Gaussian point, which can be obtained from equation (1.3.7), and can be written as
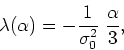
we see that the two results are identical except for the exchange of
![]() and
and
![]() . Therefore, the two results
for the slope of the critical curve at the Gaussian point coincide within
the expected level of precision of the mean-field approximation, since
the mean-field result is just an approximation, while the perturbative
result of the Gaussian approximation is, for this particular quantity,
presumably exact.
. Therefore, the two results
for the slope of the critical curve at the Gaussian point coincide within
the expected level of precision of the mean-field approximation, since
the mean-field result is just an approximation, while the perturbative
result of the Gaussian approximation is, for this particular quantity,
presumably exact.
We can also calculate the critical exponent of ![]() in the case of the
polynomial models. In order to do this it is necessary to expand
equation (2.3.5) up to a higher order in
in the case of the
polynomial models. In order to do this it is necessary to expand
equation (2.3.5) up to a higher order in ![]() , so
as to allow us to write the differential of
, so
as to allow us to write the differential of
![]() as a function of
as a function of ![]() e
e
![]() . This is the work
proposed in problem 2.3.10, and it can be shown
that it is possible to write the differential of
. This is the work
proposed in problem 2.3.10, and it can be shown
that it is possible to write the differential of ![]() as
as
where the coefficients ![]() e
e ![]() are finite and
non-vanishing expressions in the vicinity of the critical curve. The fact
that we are able to write the differential of
are finite and
non-vanishing expressions in the vicinity of the critical curve. The fact
that we are able to write the differential of ![]() directly in
terms of the differentials of
directly in
terms of the differentials of ![]() and
and ![]() with coefficients
that are finite and not zero over the critical curve is sufficient to
show that the critical exponent of
with coefficients
that are finite and not zero over the critical curve is sufficient to
show that the critical exponent of ![]() is, once more,
is, once more, ![]() .
.
In conclusion, we have discovered that the mean-field method is related,
through its generalizations, to systems on finite lattices with fixed and
self-consistent boundary conditions. These systems define a second family
of continuum limits for the models, which does not necessarily have to be
identical to the one defined by the systems with periodical boundary
conditions. Although the two families of limits have, by and large,
similar properties, many of the details are not identical and some
quantities of interest may, in fact, depend on the boundary conditions.
For example, it may be that only part of the discrepancies shown in
table 2.3.1 for the critical points of the Ising models
is due to the fact that we are using the ![]() mean-field approximation
in the right-hand column. Another part of the discrepancies may be due to
the fact that we are comparing results for systems with very different
boundary conditions, since the left-hand column refers to systems with
periodical boundary conditions. A situation like this is probably more
likely to be realized for the finer, more delicate observables, such as
the critical exponents and correlation functions, than for the more basic
objects such as the critical points.
mean-field approximation
in the right-hand column. Another part of the discrepancies may be due to
the fact that we are comparing results for systems with very different
boundary conditions, since the left-hand column refers to systems with
periodical boundary conditions. A situation like this is probably more
likely to be realized for the finer, more delicate observables, such as
the critical exponents and correlation functions, than for the more basic
objects such as the critical points.
The choice of boundary conditions is an important subject within the structure of the quantum theory, just as it is in the classical theory. It should be noted that there are other ways, besides the one that we examined here, to implement fixed boundary conditions, some of which may be physically more natural and compelling from the point of view of quantum field theory. One example of this kind of thing was proposed in the last chapter of a previous volume of this series of books [35]. Other ideas related to that one may be discussed in future volumes.
![\begin{displaymath}
\sum_{k=0}^{\infty}\frac{(2d \beta\nu_{R})^{2k+1}}{(2k+1)!}
\left[(2k+1)-2d \beta\right]=0.
\end{displaymath}](img505.gif)
Observe that all the factors in each term of this series are always
positive except for the last one on the right. Use this fact to determine
the interval of values of ![]() for which it is possible to have
for which it is possible to have
![]() and therefore
and therefore ![]() different from zero as a
solution of this equation, and thus determine the mean-field critical
points
different from zero as a
solution of this equation, and thus determine the mean-field critical
points ![]() of the Ising models.
of the Ising models.
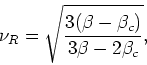
which has the correct behavior for ![]() close to
close to ![]() and that
tends to
and that
tends to ![]() for
for
![]() .
.
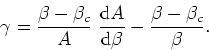
In the vicinity of the critical point we have
![]() and
and
![]() , so that we may write for
, so that we may write for ![]()
In order to calculate
![]() , differentiate
equation (2.3.1) with respect to
, differentiate
equation (2.3.1) with respect to ![]() , and thus obtain
the result
, and thus obtain
the result
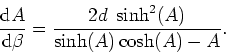
Use this in the expression for ![]() and expand it to second order
around the critical point, then use the result
and expand it to second order
around the critical point, then use the result
![]() , in
order to obtain for
, in
order to obtain for ![]() the expression
the expression
Note that, given the second-order nature of the phase transition in these
models, we know that ![]() must be within the interval
must be within the interval ![]() .
Examine the behavior of this expression in the cases
.
Examine the behavior of this expression in the cases
![]() and
and ![]() , and show by reduction to absurd that the only
possible value for the critical exponent is
, and show by reduction to absurd that the only
possible value for the critical exponent is ![]() . Substitute this
value in the equation above and obtain the value of the constant
. Substitute this
value in the equation above and obtain the value of the constant ![]() ,
thus reproducing equation (2.3.4) which was
derived in the text.
,
thus reproducing equation (2.3.4) which was
derived in the text.
![\begin{displaymath}
\frac{1}{2d}=\frac{\displaystyle \sum_{k=0}^{\infty}\frac{(2...
...\left[(d+\alpha/2)\varphi^{2}+(\lambda/4)\varphi^{4}\right]}}.
\end{displaymath}](img525.gif)
The integrals may now be written in terms of the parabolic cylinder
functions ![]() [15], so use them to
write the final form of the equation
[15], so use them to
write the final form of the equation
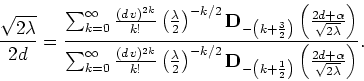
Observe that this result is the same of problem 2.3.5
if we truncate the two series that appear there, leaving only their first
terms, those with ![]() .
.
![\begin{displaymath}
\int_{0}^{\infty}{\rm d}\varphi\;\varphi^{2}
\;e^{-\left[(d+...
...{-\left[(d+\alpha/2)\varphi^{2}+(\lambda/4)\varphi^{4}\right]}
\end{displaymath}](img530.gif)
and differentiate implicitly in terms of ![]() e
e
![]() , applying the resulting coefficients at the Gaussian point.
The integrals that appear in these coefficients are expressible in terms
of the
, applying the resulting coefficients at the Gaussian point.
The integrals that appear in these coefficients are expressible in terms
of the ![]() function [14], so use them
to obtain
function [14], so use them
to obtain
Integrate this first-order differential equation for
![]() with the boundary condition
with the boundary condition ![]() , thus obtaining the final
result
, thus obtaining the final
result
Obtain the same result in another way, using in
equation (2.3.8) the asymptotic expansion of
![]() [25], since for
[25], since for
![]() the arguments of the
the arguments of the ![]() functions that appear in that
equation go to infinity.
functions that appear in that
equation go to infinity.
![\begin{eqnarray*}
\lefteqn{v_{R}\int_{0}^{\infty}{\rm d}\varphi\;\cosh(B)
\;e^{-...
...^{-\left[(d+\alpha/2)\varphi^{2}+(\lambda/4)\varphi^{4}\right]},
\end{eqnarray*}](img535.gif)
where
![]() . Then differentiate in terms of
. Then differentiate in terms of
![]() and
and
![]() , keeping in mind that
, keeping in mind that ![]() is a
function of
is a
function of ![]() and
and ![]() , in order to write the differential of
, in order to write the differential of
![]() in terms of its gradient as
in terms of its gradient as
where the coefficients are given by
![\begin{eqnarray*}
C_{0} & = & \int_{0}^{\infty}{\rm
d}\varphi\;e^{-\left[(d+\alp...
...ht]} & &
\times\left[v\;\cosh(B) -\;\varphi\;\sinh(B)\right].
\end{eqnarray*}](img537.gif)
Next expand the hyperbolic functions in each one of these coefficients
for small values of ![]() , that is, in the vicinity of the critical curve.
Observe that it is enough to expand
, that is, in the vicinity of the critical curve.
Observe that it is enough to expand ![]() e
e ![]() to first order but
that
to first order but
that ![]() must be expanded to the next non-vanishing order, because
the equation of the critical curve implies that the terms of orders zero
and one of its expansion cancel each other. In this way, obtain the
differential of
must be expanded to the next non-vanishing order, because
the equation of the critical curve implies that the terms of orders zero
and one of its expansion cancel each other. In this way, obtain the
differential of ![]() as
as
where the coefficients, which define the gradient of ![]() , are
given by
, are
given by
![\begin{eqnarray*}
C_{\alpha} & = & \frac{\displaystyle \frac{1}{3d}\int_{0}^{\in...
...-\left[(d+\alpha/2)\varphi^{2} +(\lambda/4)\varphi^{4}\right]}}.
\end{eqnarray*}](img541.gif)
Stating from these expressions verify that ![]() and
and ![]() are finite and non-vanishing numbers in the vicinity of the critical
curve. This suffices to show that the critical exponent of
are finite and non-vanishing numbers in the vicinity of the critical
curve. This suffices to show that the critical exponent of ![]() is
once again
is
once again ![]() when we approach the critical curve in the
parameter plane of the model, from any direction within the
broken-symmetrical phase. Verify also that these two coefficients are
negative, showing that the gradient of
when we approach the critical curve in the
parameter plane of the model, from any direction within the
broken-symmetrical phase. Verify also that these two coefficients are
negative, showing that the gradient of ![]() is oriented in the
expected direction.
is oriented in the
expected direction.