The Mean Field Method

In this section we will introduce the mean-field approximation method. This is an approximation process which is not perturbative, not being based on the Gaussian model. It is a traditional approximation method of statistical mechanics, which is also useful for obtaining non-perturbative approximations in quantum field theory. It is easy to use it to obtain approximations for local quantities defined on lattice sites, such as, for example the expectation value of the field. It is a well-known fact that the results of the method tend to improve with the increasing dimension of the space where the models are defined. Usually the results are reasonably good in three dimensions and even better in four dimensions, while the method often fails completely in one and two dimensions. There are even some speculations that, for some quantities, the method becomes exact in sufficiently large dimensions. In its usual formulation this method does not establish a series of successive approximations, but rather a single approximation, making it difficult to evaluate the errors involved in this approximation. We will introduce here an extension of the method, that improves the situation and allows us to understand its bad performance for small dimensions.

The formulation we will present is specifically for systems defined on the Euclidean lattice, with interactions only between next neighbors. As we will see, it is intimately related to stochastic simulations of the systems on finite lattices in which one uses a certain type of fixed boundary conditions, which we denominate self-consistent boundary conditions. These structures on finite lattices constitute an extension of the usual mean-field method and, unlike the usual method, they give us a whole series of successive approximations. The first of them will be the usual approximation, while the subsequent approximations converge to the exact solution of the models within a finite box with fixed boundary conditions, as the lattice spacing is decreased. This extension of the method is similar, but not identical, to other well-known extensions of the traditional method in statistical mechanics, such as the Oguchi method and the Bethe, Peierls, Weiss and Kikuchi [29] method. This approximation method can be used both in the polynomial models and in the sigma models, we will assume only that we have an $O(1)$ model of scalar fields, on a lattice of dimension $d$, with the usual forms of the action. As we saw in sections 1.1 and 2.1, the action of any of these models can always be separated in two parts, a strictly local one and one involving only interactions between next neighbors, which originates from the usual kinetic term and which can be written in the form of a coupling term containing products of fields at neighboring sites. This is the type of separation of the action that will be of interest in this section.

In its original formulation, applied to a statistical-mechanic system that does not necessarily have to involve only interaction between next neighbors, the mean-filed method consists of the replacement of the interactions of a given site with all the others by an interaction between that given site and a background field that does not undergo statistical fluctuations. In a situation like this we would be typically dealing with the electromagnetic interactions between the charges located at a given site and all the other charges distributed across the crystalline lattice of a solid, whose effects on the site at issue are felt through the electromagnetic fields that each charge gives rise to. What one does in this type of approximation is to replace the fluctuating electromagnetic field generated by the set of all the other charges by a mean field that does not fluctuate. This mean field is defined at each site, representing the average collective effect of all the other sites over the charges located at that point. Naturally, in order for this scheme to be useful it is necessary that we be able to calculate the mean field in terms of the charges distributed across the crystalline lattice. The calculation of this mean field clearly involves two aspects: first, there is a sum over the volume of the lattice, in order to take into account the effect of all the other sites, which are at various distances from the site at issue; second, there is a temporal average in order to eliminate the statistical fluctuations of the field, which can be exchanged for an ensemble average, according to the usual procedure of statistical mechanics.

A realization of this idea in a model defined on the lattice, like the ones we want to deal with here, must take into account only the interactions of a given site with its next neighbors. On a cubical lattice, like the ones we have been using, we can imagine that we define at each site an average field that represents the effect of the $2d$ next neighbors of the site. Of course in this case we are not dealing with electromagnetic interactions but with the self-interactions of the scalar field. Since this mean field does not fluctuate, from the point of view of quantum field theory it is not dynamical, and hence it should be treated like an external field $j_{\rm MF}$, that couples to the field $\varphi$ of the site at issue by means of an action term of the type $j_{\rm MF}\varphi$. Naturally, in order for this scheme to be useful it is necessary to adopt some criterion to allow the calculation of the value of $j_{\rm MF}$ in terms of the collection of fields, now uncoupled, that exist at the neighboring sites. The usual mean-field method on a lattice of arbitrary size consists of the replacement, in the action, of the interaction terms of each site with its next neighbors by an interaction term of the site with a non-dynamical external field, whose value is equal to the sum of the ensemble averages of the dynamical field at the neighboring sites,

$$\sum_{\vec{n}_{\ell}}^{2d}\varphi(\vec{n})\varphi(\vec{n}_{\... ...{n}_{\ell})\rangle =2d\;\varphi(\vec{n})\langle\varphi\rangle,$$

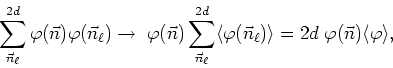
where the sum runs over the $2d$ links $\ell$ that connect the site at the position $\vec{n}$ to its next neighbors at the positions $\vec{n}_{\ell}$, and where $\langle\varphi\rangle$ is the average value of the field at any of the neighboring sites, assuming that they are all equivalent by discrete translation invariance. This means that we are using for the external field the value $j_{\rm MF}=2d\langle\varphi\rangle$. The calculation of this average value is made, in the context of this method, a-posteriori and in a self-consistent way: one calculates the average value at the active site located at $\vec{n}$ and imposes that this value be equal to the average value at the neighboring sites.

Figure 2.2.1: Lattice with $N=1$ and fixed boundary conditions, related to the usual mean-field approximation.

In this way we replace the detailed interactions between the field at each site and the fields at the neighboring sites by an interaction at each site with a background field, which does not fluctuate, thus rendering the problem mathematically more tractable. It is interesting to observe that the spirit of this approximation is somewhat different from the spirit of the usual approximation in statistical mechanics, in which we consider the interaction of the dynamical variables with an external mean field, ignoring completely that the interactions are established through the links of the lattice. Observe that, in our case here, the dimension of the lattice appears explicitly in the approximation. However, this distinction will only be really relevant when we consider the extension of the method to clusters of sites. For the case discussed so far, in which only the field at a single site is kept active, that is, undergoing statistical fluctuations, the two methods are identical. They are known in statistical mechanics as the constant coupling method, which was developed by Yvon, Nakamura, Kasteleijn, Van Kranendonk, Kikuchi and Callen [29].

This replacement of the interactions between next neighbors by an interaction with a non-dynamical field that undergoes no fluctuations is clearly a very radical change and it is rather surprising that it can produce good results, even if only for some observables. In particular, since the dynamical fields at each site interact only with the constant background field and no longer with each other, it is clear that the fields at the various sites will become completely uncorrelated from each other in this approximation, so that the calculation of correlation functions is out of the question. There is, however, an alternative interpretation of the method, which will allow us to extend it to clusters of active sites and hence to recover the correlations among sites. This alternative interpretation, which changes nothing in the mathematics involved, is that the fields at all the sites are frozen at their average values, except for a single arbitrarily chosen site, which remains active. Since in the traditional mean-field method all the sites are equivalent and uncorrelated from each other, any result obtained for one of them is valid for all the others. Therefore, in the traditional method it is sufficient to keep a single active site, without any changes in the results, which establishes the equivalence of the two interpretations. In any of the two interpretations the dynamical fields interact only with a constant background field, independently of how we interpret this non-dynamical field, either as an external field or as the field of the neighboring sites.

Figure 2.2.2: Lattice with $N=2$ and fixed boundary conditions, which constitutes the first extension of the mean-field method.

The resulting structure, in this second interpretation, is a lattice with $N=1$ and a border where the field is kept fixed at its average value, just like the lattices with fixed boundary conditions that we have seen before in [32], [33] and [34], which are represented as in the diagram in figure 2.2.1, including the active site and the border sites. In any of the two interpretations the mathematical consequence of the approximation is that the infinite-dimensional functional integral on the lattice is replaced by a one-dimensional integral over the dynamical field at the only remaining active site,

$$\frac{\displaystyle \int[{\bf d}\varphi]\;{\cal O}[\varphi]\... ...}{\displaystyle \int{\rm d}\varphi\;e^{-S_{\rm MF}(\varphi)}},$$ (2.2.1)

where $S_{\rm MF}$ is the mean-field approximation for the lattice action and ${\cal O}(\varphi)$ is some observable that depends only on the field at the single remaining active site. It is usually possible to calculate analytically the resulting integral, which establishes the usefulness of the method in its conventional form.

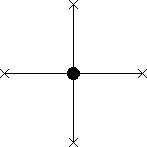
This second interpretation of the method suggests at once the definition of a series of approximations of the continuous system, of which the usual mean-field method is the first. Just consider lattices in which more than one site is left active, within a central cluster, while the fields at the borders are kept fixed. For example, we may consider a sequence $N=1,2,3,\ldots$ of cubical lattices, such that the second approximation, with $N=2$, is given by the lattice illustrated in figure 2.2.2, with $2^{d}$ sites, all in direct contact with the border.

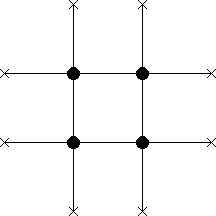
This extension of the mean-field method is similar to the method of clusters of Bethe, Peierls, Weiss and Kikuchi in statistical mechanics, in which groups of connected sites are considered. The first cluster considered in this method is the Bethe-Peierls cluster, which is shaped like a diamond as shown, within the context of our lattice representation, by the diagram in figure 2.2.3, including the border sites, which are not part of the original cluster method. Larger clusters with formats similar to this one may also be considered and used for analytical calculations. However, the amount of analytical work involved is usually quite large, to achieve only modest gains in the quality of the results obtained.

In the general case our extension is not identical to the traditional cluster method, because in our case the interaction of the cluster with the mean field is established only through the border, not by means of an external mean field that acts also on the internal sites of the cluster, which have no direct contact with the border. This kind of internal site appears in the Bethe-Peierls cluster and also in the cubical clusters starting from $N=3$, as illustrated in the diagram in figure 2.2.4. The two methods also differ regarding the type of self-consistency condition which is imposed. In the case of the Bethe-Peierls cluster, rather than adjusting the external mean field so that it becomes consistent with the average value of the fields at the active sites, what is done is to adjust it so that the average of the field at the central site is identical to the average of the field at the other $2d$ sites of the cluster, which are all equivalent to each other due to the symmetry of the cluster. Hence, what one actually imposes in this case is that the normal derivative of the average value of the field vanish at the border.

Figure 2.2.3: Modified lattice used in the Bethe-Peierls cluster method.

It is clear that the $N\rightarrow\infty$ limit of our sequence of cubical clusters produces exactly the continuum limit within a finite cubical box with a certain type of self-consistent boundary conditions. Let us now discuss, in greater detail, the self-consistency condition to be imposed on the border sites. The usual $N=1$ mean-field approximation is sufficient for the calculation of strictly local quantities, defined at a single site. These calculations may always be performed by freezing the fields at the sites of the border at some arbitrary value, thus leaving a single active site. One calculates then the average value of the field at the active site, by means of the integral that appear in equation (2.2.1), using ${\cal O}(\varphi)=\varphi$. Having done this, one compares the result obtained, which will depend on the value that was chosen for the fields at the border, with that value. Of course in general they will be different and the self-consistency problem is to find the value to be used at the border that reproduces exactly the same value for the average value of the dynamical field at the active site. The determination of the value of the mean field by a self-consistent procedure like this was first introduced in the case of the constant coupling method of statistical mechanics.

Figure 2.2.4: Lattice with $N=3$ and fixed boundary conditions, which constitutes the second extension of the mean-field method.

In an analytical calculation one can simply impose this condition a posteriori, so that it results in an algebraic equation for the average value of the field. Once this equation is solved and the average value of the field is found in terms of the parameters of the model, mean-field approximations for other quantities may also be obtained. The same self-consistency condition can also be imposed in the context of a Monte Carlo simulation in which the filed at the border is kept at a constant value, without fluctuations, either for $N=1$ or for larger values of $N$. In this numerical approach a negative feedback mechanism can be used to slowly adjust the value of the field at the border so that it and the average value of the field measured in the interior of the lattice converge to a common limiting value. We denominate this special type of fixed boundary conditions self-consistent boundary conditions.

The stochastic simulation with $N=1$ is equivalent to a Monte Carlo calculation of the integral that appears in equation (2.2.1). In this case the feedback mechanism can be implemented is a very simple way. One puts at the border fields a tentative value and lets the dynamical field fluctuate. One then measures the average value of the fluctuating field at the active site. If this average value differs from the tentative value at the border, the value at the border is modified so as to coincide with the value measured in the interior. This is done many times at regular intervals, so that eventually the adjustment of the value at the border becomes negligible and the border fields stay at the desired value. From this moment on one can start measuring whatever observables one may be interested in. For lattices larger than that of the case $N=1$ a similar mechanism may be used, but this time there are several possible variations of the procedure. For example, we may measure and feed back to the border the average value calculated for the spacial average of the fields over all the internal sites or, alternatively, we may use a spacial average over only the internal sites which are in direct contact with the border, thus implementing a self-consistency condition in the spirit of the Bethe-Peierls condition, involving the normal derivative at the border.

One of the most interesting properties of these systems with fixed but self-consistent boundary conditions relates to their characteristics of critical behavior. Usually we build the models and their corresponding stochastic simulations on finite lattices with periodical boundary conditions^2.1. These systems suffer from the inconvenience that there is no true critical behavior on finite lattices of this kind, that is, in systems with a finite number of degrees of freedom and no external boundary [30]. For example, if we calculate by means of stochastic simulations on finite lattices the expectation value $v_{R}$ of the field in the Ising models, a quantity which is analogous to the magnetization, as a function of the inverse temperature $\beta$, we typically obtain curves $v_{R}(\beta)$ that are continuous, differentiable and monotonically increasing. There are no sharp transitions except in the $N\rightarrow\infty$ limit, which makes it considerably more difficult to extract from these simulations the critical values of the parameters of the models by means of extrapolations of the finite-lattice results to the $N\rightarrow\infty$ limit.

In contrast to this, the self-consistent lattice systems display sharp transitions and complete critical behavior even on finite lattices. In the case $N=1$ the fact that the curve of the magnetization displays a sharp transition at a certain critical value of $\beta$, a point where it is not differentiable, can be verified analytically. In numerical simulations the sharpness of the transitions is limited, of course, by the technical and numerical limitations of the computer simulations but, with increasing expenditure of computer resources, the transitions can, at least in principle, be made as sharp as one desires for any given $N$, quite unlike the case of periodical simulations. These self-consistent simulations are, therefore, potentially better for the calculation of critical quantities. With simulations for larger values of $N$ we can not only improve the calculation of local quantities such as the expectation value of the field, we can also calculate significant approximations for non-local quantities, such as the correlation functions for the theory defined within a finite box. This is, therefore, a very useful extension of the mean-field method. Clearly, there is a numerical price to be paid for the sharpness of the transitions obtained in this way. The feedback mechanism can consume a large amount of computer resources if we want really very sharp results, specially in simulations that already suffer from the notorious critical slowing down problems near the critical region. Fortunately, there exist currently algorithms that avoid completely this kind of problem for the scalar models that we are examining here.

Observe that we have here a set of systems with a finite number of degrees of freedom that still display complete critical behavior. How to reconcile this fact with the previously mentioned fact that there is no true critical behavior in systems with a finite number of degrees of freedom? What happens is that the relevant results contained in [30] are not relevant for the self-consistent systems, because they assume that one is discussing systems with a finite number of degrees of freedom and no external couplings, which implies that one must use periodical boundary conditions in order to avoid the border. In our fixed-boundary systems there is an additional element, which is precisely the interaction with the border sites, for which there is a self-consistent condition. In a heuristic and intuitive way, we may think of these systems as finite systems that have, however, a ``window to infinity''. The self-consistent boundary conditions act in fact as a kind of semi-transparent window opening onto an infinite outer lattice that surrounds our finite lattice, letting in some information about the infinite lattice of which our finite lattice is a cutout. It would be possible, in fact, to consider other types of boundary fixed conditions, more complex, sophisticated and transparent than the one we are considering here. For example, instead of keeping the boundary fields completely fixed at their mean values, we might consider letting them fluctuate around the mean value in some controllable way. In the future we may discuss in more detail a proposal along these general lines. But before that we must illustrate the method by means of some specific calculations with self-consistent boundary conditions.

Our extension of the method to lattices of arbitrary size provides us with an explanation of why the usual mean-field method fails completely for most models in dimensions $d=1$ and $d=2$. For this purpose it is necessary to remember that these are models that do not display phase transition in the $N\rightarrow\infty$ limit. In fact, there are theorems [31] that show that models with only next-neighbor couplings cannot have ordered phases, with oriented fields, in the $N\rightarrow\infty$ limit, in dimension $d=1$, for any symmetry groups they may be invariant by. For dimension $d=2$ the same is true for models invariant by continuous symmetry groups, such as $SO(\mathfrak{N})$ for $\mathfrak{N}>1$. For discrete symmetry groups the existence of oriented phases is possible in $d=2$, as shown by the Ising model, with the discrete symmetry group $O(1)=\mathbb{Z}_{2}$. There are no theorems like these for $d\geq 3$, cases in which the models usually display well-defined phase transitions in the $N\rightarrow\infty$ limit.

Let us see how these theorems are realized for the models defined on finite lattices of increasing size. The situation is similar in the cases of periodical boundary conditions and of fixed boundary conditions, but it is easier to give the explanation in the case of fixed boundary conditions. In this case one verifies that the models always display a phase transition on finite lattices, for any model and any space-time dimension. In this way a certain $\beta_{c}(N)$ is defined on each finite lattice, which is the critical point for that lattice size, assuming that we use as an example a sigma or Ising model. In the cases in which there is a phase transition in the $N\rightarrow\infty$ limit $\beta_{c}(N)$ tends to a finite value $\beta_{c}^{*}$ when $N\rightarrow\infty$. In the cases in which there is no phase transition in the limit what happens is that $\beta_{c}(N)$ increases without limit when $N$ goes to infinity. Since in all cases we have the non-oriented phase for $\beta<\beta_{c}$, in these cases this random phase is the only one that remains in the $N\rightarrow\infty$ limit.

Thus we see that, if there is a phase transition for some well-defined finite $\beta_{c}^{*}$ in the $N\rightarrow\infty$ limit, then the $N=1$ approximation, which also displays a well-defined phase transition, will not be qualitatively different from the limit, although it may be quantitatively quite different, thus giving rise to an approximation that is interpreted as successful. In contrast to this, in the case in which there is no phase transition in the limit $N\rightarrow\infty$ the $N=1$ approximation, because it always displays a well-defined phase transition, becomes qualitatively different from the limit and is thus interpreted as a complete failure. Observe that the $N=1$ approximation fails precisely in the cases in which the system does not display critical behavior in the limit of large values of $N$, cases which are not, therefore, of much interest for us.

The situation regarding the realization of the theorems is not very different for periodical boundary conditions, except for the fact that in this case there are no well-defined critical points on finite lattices. However, in order to tackle this case, we must first dispel a common misconception regarding finite lattice systems with periodical boundary conditions. Although it is true that if one measures the expectation value of the field $v_{R}$ in such systems one gets zero within errors, this does not really mean that the single phase existing on finite lattices is the symmetrical phase. The reason why one gets zero for $v_{R}$ in these circumstances is not that the field configurations are typically non-oriented, but rather that the average value us washed out by the wandering of the direction of alignment. The best way to describe what happens is to say that the system is always in the broken-symmetrical phase on finite lattices, and that it only becomes symmetrical in a certain region of its parameter space in the $N\rightarrow\infty$ limit.

One can verify this fact in at least three ways, which we now describe shortly. First, one can include in the action a constant external action $j$ and verify that the resulting value of $v_{R}$ does not vanish in the limit in which $j\rightarrow 0$. Second, one can consider looking at the expectation value of the average of the field over the lattice, which is just the zero mode, the zero-momentum Fourier transform $\widetilde\varphi (\vec{0})$ which is like the magnetization in statistical mechanics; if one measures both its expectation value and the expectation value of its square, one gets zero for the first but not for the second, meaning that the field configurations are typically oriented, and that the direction of this orientation drifts. Third, one can eliminate the drift on finite lattices by hand by freezing the zero mode of the field in an arbitrarily chosen direction, and then verifying that one gets explicitly a non-vanishing average magnetization; this changes nothing in the $N\rightarrow\infty$ limit, since in this limit the drift is frozen in any case.

Getting back to our explanation of the realization of the theorems for the models defined on finite periodical lattices, in this case the system is always in a single broken-symmetrical phase, and taking due care with the drift of the zero-mode one can measure $v_{R}$ as a function of $\beta$. The function $v_{R}(\beta)$ turns out to be a continuous and differentiable function, which is never zero, being typically small in the range of the parameters of the model where the symmetrical phase will appear in the $N\rightarrow\infty$ limit, and typically large in the complementary range. What happens in the $N\rightarrow\infty$ limit, when there is a phase transition, is that the curve $v_{R}(\beta)$ gradually changes and thus approaches a continuous but non-differentiable curve in the limit. The point where the curve becomes non-differentiable is the critical point and, in this case, it appears at finite values of the parameters. In the cases in which the system does not display a phase transition in the limit the curve not only changes shape, but also moves to arbitrarily large values of beta, so that once more all that remains in the limit is a symmetrical, non-oriented phase.

Finally, observe that we are not stating here that the continuum limits of the periodical systems and of the self-consistent systems are completely identical, because some of the observables may depend on the boundary conditions adopted, which are different in either case. These are two different classes of continuum limits, whose properties can be somewhat different. Usually the more basic observables of the system, such as the values of the parameters at the critical points, the renormalized masses and the expectation values of the fields, will not depend significantly on the boundary conditions, but observables with a subtler type of behavior, such as the critical exponents, may very well depend strongly on the boundary conditions. In fact, one can show that the critical exponents differ significantly in the two cases that we are discussing here. Besides the fact that fixing the field at the border does not make much physical sense in the context of quantum field theory, this is another reason why it is important to think about generalizations of the self-consistent boundary conditions described here, for example in order to allow the border fields to fluctuate, as was mentioned before in this section. This subject may be discussed in more detail in a future volume of this series.