Next: The Mean Field Method Up: The Sigma-Model Limit Previous: The Sigma-Model Limit Contents
In this section we will take the
![]() limit of the
limit of the
![]() model. This can be done for more general models than
the one-component
model. This can be done for more general models than
the one-component
![]() model we are examining here,
namely the multi-component
model we are examining here,
namely the multi-component
![]() models which are
invariant by the
models which are
invariant by the
![]() groups of transformations. In general the
groups of transformations. In general the
![]() limit of these models will take us to the
corresponding
limit of these models will take us to the
corresponding
![]() -invariant sigma models. In our case here, however,
we will deal only with the one-component
-invariant sigma models. In our case here, however,
we will deal only with the one-component
![]() , which is
invariant by the sign reflections. The simple discrete set of
transformations given by the identity and the reflection also forms a
group of transformations, a discrete group which is known by either
, which is
invariant by the sign reflections. The simple discrete set of
transformations given by the identity and the reflection also forms a
group of transformations, a discrete group which is known by either
![]() or
or
![]() . In this case the corresponding sigma model is
simply the Ising model which was mentioned
in [13]. In this way we will establish that we
can use the Ising model as a direct representation of the
infinite-coupling limit of the
. In this case the corresponding sigma model is
simply the Ising model which was mentioned
in [13]. In this way we will establish that we
can use the Ising model as a direct representation of the
infinite-coupling limit of the ![]() -symmetrical
-symmetrical
![]() model.
model.
 |
The Ising model can be obtained from the
![]() polynomial
model in the limit in which the coupling parameter
polynomial
model in the limit in which the coupling parameter ![]() tends to
positive infinity over negative-slope straight lines in the parameter
plane of the
tends to
positive infinity over negative-slope straight lines in the parameter
plane of the
![]() model. These lines must exist only for
model. These lines must exist only for
![]() , because otherwise they would cross the region where the
model is unstable. Also, their slopes must be strictly negative (not
zero) and finite, which rules out horizontal and vertical lines in the
parameter plane. Since the slopes must be strictly negative and finite,
in these limits we will have
, because otherwise they would cross the region where the
model is unstable. Also, their slopes must be strictly negative (not
zero) and finite, which rules out horizontal and vertical lines in the
parameter plane. Since the slopes must be strictly negative and finite,
in these limits we will have
![]() and
and
![]() in such a way that
in such a way that
![]() is a
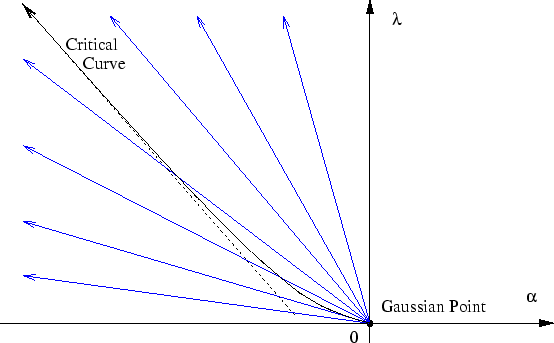
positive constant. Figure 2.1.1
illustrates the situation for lines starting from the Gaussian point.
Observe that in these limits only the slope of the lines really
matters. It makes no difference whether we use
is a
positive constant. Figure 2.1.1
illustrates the situation for lines starting from the Gaussian point.
Observe that in these limits only the slope of the lines really
matters. It makes no difference whether we use
![]() or
or
![]() for some finite constant
for some finite constant ![]() , because
the finite additional term becomes irrelevant in the limit. In fact, we
may take the limit over any curve that approaches asymptotically a
negative-slope straight line. An important example of this is the
critical curve of the
, because
the finite additional term becomes irrelevant in the limit. In fact, we
may take the limit over any curve that approaches asymptotically a
negative-slope straight line. An important example of this is the
critical curve of the
![]() model, which in the
model, which in the
![]() limit approaches the critical point of the
corresponding Ising model.
limit approaches the critical point of the
corresponding Ising model.
In order to establish this connection between the two models we start by
recalling that the action of the
![]() model without
external sources, as it was defined in section 1.1, is given by
model without
external sources, as it was defined in section 1.1, is given by
![\begin{displaymath}
S[\varphi]=\frac{1}{2}\sum_{\ell}(\Delta_{\ell}\varphi)^{2}
...
...um_{s}\varphi^{2}(s)
+\frac{\lambda}{4}\sum_{s}\varphi^{4}(s).
\end{displaymath}](img348.gif)
As we already discussed in section 1.1, we may now separate the
action of the model in two parts, a kinetic part ![]() containing only
the derivative terms,
containing only
the derivative terms,
![\begin{displaymath}
S_{K}[\varphi]=\frac{1}{2}\sum_{\ell}(\Delta_{\ell}\varphi)^{2},
\end{displaymath}](img349.gif)
and a potential part ![]() containing the polynomial terms,
containing the polynomial terms,
![\begin{displaymath}
S_{V}[\varphi]=\sum_{s}V(\varphi),\mbox{ where }
V(\varphi)=\frac{\alpha}{2}\varphi^{2}+\frac{\lambda}{4}\varphi^{4}.
\end{displaymath}](img350.gif)
The functional integrals that appear in the definition of the observables of the quantum theory may now be written as
so that, including the exponential of ![]() in the measure of the
distribution of the model, we may write this distribution as
in the measure of the
distribution of the model, we may write this distribution as
Since we may multiply this quantity by any constant independent of the fields without changing the observables, we may write the measure as
where
![]() is the local part of the
distribution, which we thus include in the measure, normalized as
is the local part of the
distribution, which we thus include in the measure, normalized as
Observe that the integration runs only over the positive values of
![]() and hence can be interpreted as an integration over the
absolute value of the field. With this the following normalization
condition for
and hence can be interpreted as an integration over the
absolute value of the field. With this the following normalization
condition for ![]() holds,
holds,
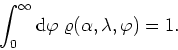
The integration over the absolute value of the field, when generalized to
the more complex models having
![]() symmetry, corresponds to the
separation of the integration variables into a radial part and an angular
part. In this way the arguments being presented here can be easily
generalized to that case. In general the radial variable will be the
modulus of the
symmetry, corresponds to the
separation of the integration variables into a radial part and an angular
part. In this way the arguments being presented here can be easily
generalized to that case. In general the radial variable will be the
modulus of the ![]() -dimensional field vector in the internal symmetry
space, which in our case here reduces to the absolute value of
-dimensional field vector in the internal symmetry
space, which in our case here reduces to the absolute value of
![]() . Also, in our discrete
. Also, in our discrete ![]() -symmetrical case the integral
over the angular part reduces to a sum over only two points,
corresponding to rotations by each one of the two angles
-symmetrical case the integral
over the angular part reduces to a sum over only two points,
corresponding to rotations by each one of the two angles ![]() and
and ![]() ,
and hence to the two possible signs,
,
and hence to the two possible signs, ![]() and
and ![]() .
Therefore, in our present case the integral over all the values of
.
Therefore, in our present case the integral over all the values of
![]() at each site is being decomposed in this way into an integral
over the positive values of
at each site is being decomposed in this way into an integral
over the positive values of ![]() and a sum over the two possible
signs. Since both
and a sum over the two possible
signs. Since both
![]() and
and ![]() are
even functions of
are
even functions of ![]() , they are in fact functions only of the
absolute value of
, they are in fact functions only of the
absolute value of ![]() , and independent of its sign, so it is not
necessary to make their dependence on the absolute value explicit. Given
all this, we may write the functional integrals as
, and independent of its sign, so it is not
necessary to make their dependence on the absolute value explicit. Given
all this, we may write the functional integrals as
where
![]() represents the sum over all the possibilities
for combinations of the sign of the field at each site, over all sites.
Writing this functional integral explicitly this once, for clarity, we
have
represents the sum over all the possibilities
for combinations of the sign of the field at each site, over all sites.
Writing this functional integral explicitly this once, for clarity, we
have
![\begin{displaymath}
\int[{\bf d}\varphi\;\varrho(\alpha,\lambda,\varphi)]\;e^{-S...
...[\alpha,\lambda,\varphi(s)]
\right\}\;e^{-S_{K}[\psi\varphi]},
\end{displaymath}](img365.gif)
where ![]() is a new variable holding the sign of the field at the
site
is a new variable holding the sign of the field at the
site ![]() , while
, while ![]() assumes only positive values, due to the limits
of integration adopted.
assumes only positive values, due to the limits
of integration adopted.
Let us now examine the behavior of
![]() when
when
![]() and
and
![]() , for some positive
, for some positive
![]() . Note that, since lines making angles
. Note that, since lines making angles ![]() and
and ![]() with the
with the
![]() coordinate axis are excluded, so are the corresponding values
coordinate axis are excluded, so are the corresponding values
![]() and
and ![]() . Executing the calculation of the integral
in the denominator we obtain (problem 2.1.1), in
terms of the parabolic cylinder functions
. Executing the calculation of the integral
in the denominator we obtain (problem 2.1.1), in
terms of the parabolic cylinder functions ![]() ,
,
Using the asymptotic form of
![]() (problem 2.1.2) and substituting
(problem 2.1.2) and substituting ![]() in
terms of
in
terms of ![]() , we may write the distribution
, we may write the distribution
![]() ,
for large values of
,
for large values of ![]() , as
, as
We see here that indeed we cannot have either ![]() or
or
![]() , because in either case
, because in either case ![]() would vanish identically
and hence would cease to be a normalizable statistical distribution.
Given a finite and non-zero value of
would vanish identically
and hence would cease to be a normalizable statistical distribution.
Given a finite and non-zero value of ![]() we also see that, when
we also see that, when
![]() ,
, ![]() tends to zero for all
tends to zero for all ![]() except for
except for
![]() , where it diverges as
, where it diverges as ![]() .
Hence, given a continuous and limited function
.
Hence, given a continuous and limited function ![]() and
considering the normalization of
and
considering the normalization of ![]() , one can verify that, in the
, one can verify that, in the
![]() limit
(problem 2.1.3),
limit
(problem 2.1.3),
In other words, the distribution
![]() tends to a
Dirac delta function,
tends to a
Dirac delta function,
The conclusion is that in this limit the expectation values of the polynomial model may be written as
![\begin{displaymath}
\langle{\cal O}\rangle_{N}=\frac{\displaystyle \sum[\psi=\pm...
...i\vert\;\delta(\varphi^{2}-\beta)] \;e^{-S_{K}[\psi\varphi]}},
\end{displaymath}](img381.gif)
where the remaining part of the measure can be written explicitly as
![\begin{displaymath}[{\bf d}\vert\varphi\vert\;\delta(\varphi^{2}-\beta)]=\prod_{s}{\rm
d}\vert\varphi(s)\vert\;\delta[\varphi^{2}(s)-\beta],
\end{displaymath}](img382.gif)
where the Dirac delta functions imply a condition of constraint on the
fields,
![]() , or
, or
![]() , since the sign of
, since the sign of
![]() is being considered explicitly and hence
is being considered explicitly and hence ![]() is positive.
We may now use the Dirac delta functions to perform all the integrations
over
is positive.
We may now use the Dirac delta functions to perform all the integrations
over ![]() , thus obtaining for the expectation values
, thus obtaining for the expectation values
![\begin{displaymath}
\langle{\cal O}\rangle_{N}=\frac{\displaystyle \sum[\psi=\pm...
...\displaystyle \sum[\psi=\pm
1]\;e^{-S_{K}[\sqrt{\beta}\psi]}}.
\end{displaymath}](img386.gif)
We may now examine the form of the action ![]() under these conditions,
in order to simplify it and exhibit it in a more familiar form. In terms
of the new variables
under these conditions,
in order to simplify it and exhibit it in a more familiar form. In terms
of the new variables ![]() and the parameter
and the parameter ![]() this action can be
written as
this action can be
written as
![\begin{displaymath}
S_{K}[\psi]=\frac{\beta}{2}\sum_{\ell}(\Delta_{\ell}\psi)^{2},
\end{displaymath}](img388.gif)
where the new field variables
![]() satisfy the
constraint
satisfy the
constraint ![]() , since they are just signs, and the parameter
, since they are just signs, and the parameter
![]() appears now multiplying the action, just like the parameter
appears now multiplying the action, just like the parameter
![]() of statistical mechanics. Although we may want to think of
of statistical mechanics. Although we may want to think of
![]() as the inverse of a fictitious temperature, in order to guide our
intuition about the behavior of the models, we should remember that our
as the inverse of a fictitious temperature, in order to guide our
intuition about the behavior of the models, we should remember that our
![]() is, in truth, related to the mass parameter
is, in truth, related to the mass parameter ![]() and the
coupling constant
and the
coupling constant ![]() , and not to any truly physical
temperature related to the dynamical system we are studying. The
phenomenon that something relating to a coupling constant appears
multiplying the action due to a scaling redefinition of the fields is
typical of the gauge theories, as we may see in future volumes.
, and not to any truly physical
temperature related to the dynamical system we are studying. The
phenomenon that something relating to a coupling constant appears
multiplying the action due to a scaling redefinition of the fields is
typical of the gauge theories, as we may see in future volumes.
Note that, although ![]() is a purely quadratic functional of
is a purely quadratic functional of
![]() , the model is not the free theory, due to the fact that the
field
, the model is not the free theory, due to the fact that the
field ![]() satisfies an equation of constraint, and is not, therefore,
a free real variable. This is a situation in which the non-linearities,
instead of being introduced by a term in the action, are introduced
instead by the measure of the functional integral, which is where the
constraint is implemented in the quantum theory. We may now perform one
more transformation of the action of the model, with the intention of
showing in a clearer way its relation with the Ising model of statistical
mechanics. If we expand the squares of the derivatives contained in the
action, we get
satisfies an equation of constraint, and is not, therefore,
a free real variable. This is a situation in which the non-linearities,
instead of being introduced by a term in the action, are introduced
instead by the measure of the functional integral, which is where the
constraint is implemented in the quantum theory. We may now perform one
more transformation of the action of the model, with the intention of
showing in a clearer way its relation with the Ising model of statistical
mechanics. If we expand the squares of the derivatives contained in the
action, we get
where
![]() and
and
![]() are the fields at the two
ends of the link
are the fields at the two
ends of the link ![]() . Using now the equation of constraint
. Using now the equation of constraint
![]() we see that the two terms containing the squares are
constant, independent of the fields, which means that they can be
neglected in the action without changing the observables. We are left,
therefore, with the bilinear term, and we write the action as
(problem 2.1.4)
we see that the two terms containing the squares are
constant, independent of the fields, which means that they can be
neglected in the action without changing the observables. We are left,
therefore, with the bilinear term, and we write the action as
(problem 2.1.4)
We have here an interaction between next neighbors involving the product
of unit spins, exactly like in the Ising model. Hence we see that the
infinite coupling limit of the ![]() polynomial model is indeed the
Ising model. Therefore, the expectation values of the polynomial model
can be written as expectation values in this model, by means of a simple
rescaling of the variable appearing within the observable,
polynomial model is indeed the
Ising model. Therefore, the expectation values of the polynomial model
can be written as expectation values in this model, by means of a simple
rescaling of the variable appearing within the observable,
![\begin{displaymath}
\langle{\cal O}[\varphi]\rangle_{N}=\frac{\displaystyle \sum...
...psi=\pm
1]\;e^{\beta\sum_{\ell}\psi(\ell_{-})\psi(\ell_{+})}}.
\end{displaymath}](img398.gif)
Observe that, once the
![]() limit is taken in the
way explained here, this relationship between the two classes of models
is exact and involves no approximations of any kind.
limit is taken in the
way explained here, this relationship between the two classes of models
is exact and involves no approximations of any kind.
It is important to discuss here the situation regarding the introduction of external sources into the model in this limit. The Ising model inherits from the polynomial model the introduction of external sources by means of a linear term in the action,
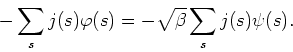
It follows therefore that, apart from a rescaling of the sources by
![]() , the introduction of external sources is to be done in the
usual way. In order to write this term in the form which is customary in
statistical mechanics, we define the external sources
, the introduction of external sources is to be done in the
usual way. In order to write this term in the form which is customary in
statistical mechanics, we define the external sources ![]() for the
Ising model as
for the
Ising model as
![]() , so that the external-source
term of the action acquires the form
, so that the external-source
term of the action acquires the form
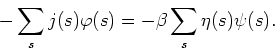
At first sight it might seem natural to include the source term of the
polynomial model in the potential part of the action, together with the
![]() and
and ![]() terms, and then to rework the derivation of the
large-coupling limit. However, this should not be done, for two reasons:
first, the external source term does not change in the limit and has in
fact no role to play in it; second, it is not simply a polynomial term in
terms, and then to rework the derivation of the
large-coupling limit. However, this should not be done, for two reasons:
first, the external source term does not change in the limit and has in
fact no role to play in it; second, it is not simply a polynomial term in
![]() , because its coefficient
, because its coefficient ![]() is not a constant like
is not a constant like ![]() or
or
![]() , but rather an arbitrary function of the sites. The
external-source term should therefore be left in the action, together
with the kinetic term
, but rather an arbitrary function of the sites. The
external-source term should therefore be left in the action, together
with the kinetic term ![]() , and should not be included in the measure
with the potential term
, and should not be included in the measure
with the potential term ![]() .
.
When the external-source term is treated in this way, the derivation of
the large-coupling limit proceeds exactly as before, nothing changes in
the derivation because no steps in it depend on other terms that the
complete action may contain, besides the potential term ![]() . We may
therefore introduce external sources into the resulting Ising model
exactly as we would do in the original polynomial model, and the whole
functional generator formalism is made available for the analysis of the
Ising model, without any change. Hence the Ising model is in fact an
exact and complete direct representation of the infinite-coupling limit
of the corresponding
. We may
therefore introduce external sources into the resulting Ising model
exactly as we would do in the original polynomial model, and the whole
functional generator formalism is made available for the analysis of the
Ising model, without any change. Hence the Ising model is in fact an
exact and complete direct representation of the infinite-coupling limit
of the corresponding
![]() polynomial model. This
relationship can be generalized to the multicomponent
polynomial model. This
relationship can be generalized to the multicomponent
![]() -invariant
polynomial models and the corresponding sigma models. It can also be
generalized to models with larger powers of the fields. It is possible to
show (problem 2.1.5) that the Ising model can also
be obtained as the
-invariant
polynomial models and the corresponding sigma models. It can also be
generalized to models with larger powers of the fields. It is possible to
show (problem 2.1.5) that the Ising model can also
be obtained as the
![]() limit of the
limit of the
![]() polynomial models, with
polynomial models, with
![]() , in a way
which is completely analogous to the
, in a way
which is completely analogous to the ![]() case that we examined here.
case that we examined here.
Another aspect which we must examine here is the one relating to the
superposition process involved in the definition of the block variables.
Once again this is inherited by the Ising model from the polynomial
model, so we still have a simple linear superposition of the fields
![]() at the various sites within the block. Note that although these
fundamental fields satisfy the constraint
at the various sites within the block. Note that although these
fundamental fields satisfy the constraint ![]() , the same will not
be true for the block variables. If we consider the process of linear
superposition of the fields within a block, in order to define a block
variable, it is evident (problem 2.1.6) that the
sum and the average of a collection of signs
, the same will not
be true for the block variables. If we consider the process of linear
superposition of the fields within a block, in order to define a block
variable, it is evident (problem 2.1.6) that the
sum and the average of a collection of signs ![]() will not itself
have unit absolute value. If the fields are distributed is a very random
way, without any appreciable alignment, their average will tend to have
an absolute value much smaller than
will not itself
have unit absolute value. If the fields are distributed is a very random
way, without any appreciable alignment, their average will tend to have
an absolute value much smaller than ![]() . Only in the opposite case, when
the fields are highly aligned, the absolute value of the average will
tend to
. Only in the opposite case, when
the fields are highly aligned, the absolute value of the average will
tend to ![]() . The absolute value of the sum may have any value, either
larger or smaller than
. The absolute value of the sum may have any value, either
larger or smaller than ![]() .
.
We see therefore that in general the introduction of external sources
will cause the block variables, which are the variables in terms of which
we should interpret the theory, to deform to any value, without
respecting an equation of constraint. In fact, they will behave much like
the corresponding variables of the polynomial models. In short, we see
that the constraint that appears for the fundamental field in the
large-coupling limit does not survive the block-variable superposition
process and that the Ising model we get in the limit is not fundamentally
different from the
![]() polynomial model it derives
from. Hence we confirm that the Ising models are not to be seen as a
completely different class of models, but as a way to examine directly
the behavior of the polynomial models in the
polynomial model it derives
from. Hence we confirm that the Ising models are not to be seen as a
completely different class of models, but as a way to examine directly
the behavior of the polynomial models in the
![]() limit. Since, as was mentioned before, the Ising models can also be
obtained as the limits of the
limit. Since, as was mentioned before, the Ising models can also be
obtained as the limits of the
![]() polynomial models for
any
polynomial models for
any ![]() , they become a tool for the examination of the
large-coupling limit of a large class of models.
, they become a tool for the examination of the
large-coupling limit of a large class of models.
We will finish this section with some comments about the critical
behavior of the models. As we shall see later, approximate calculations
based on the mean-field technique show that the Ising models have
well-defined critical points ![]() for dimensions
for dimensions ![]() . Since
they are the
. Since
they are the
![]() limits of the polynomial models,
we see that the perturbative Gaussian approximation also predicts
well-defined critical points for the Ising models, although they are
infinitely distant from the Gaussian point. In fact, the two predictions
do not differ very much from each other, and are both confirmed
qualitatively by the computer simulations. In each dimension
limits of the polynomial models,
we see that the perturbative Gaussian approximation also predicts
well-defined critical points for the Ising models, although they are
infinitely distant from the Gaussian point. In fact, the two predictions
do not differ very much from each other, and are both confirmed
qualitatively by the computer simulations. In each dimension ![]() we
have therefore the same situation, a critical line in the parameter plane
of the polynomial model, connecting at one end with the Gaussian point at
the origin, and connecting at the other end with the critical point of
the Ising model, over the arc at infinity.
we
have therefore the same situation, a critical line in the parameter plane
of the polynomial model, connecting at one end with the Gaussian point at
the origin, and connecting at the other end with the critical point of
the Ising model, over the arc at infinity.
The situation for ![]() is very peculiar in the case of the
is very peculiar in the case of the ![]() models
and deserves to be mentioned here. In this case the polynomial model does
not exist in the vicinity of the Gaussian point, except for the Gaussian
point itself. There is, therefore, no critical line connecting the
Gaussian point to the critical point of the two-dimensional Ising model,
which does exist, however, as is well known. In the corresponding
models
and deserves to be mentioned here. In this case the polynomial model does
not exist in the vicinity of the Gaussian point, except for the Gaussian
point itself. There is, therefore, no critical line connecting the
Gaussian point to the critical point of the two-dimensional Ising model,
which does exist, however, as is well known. In the corresponding
![]() model there is a convergent expansion near the
Gaussian point [28], which shows that
the observables are analytical functions of the parameters and that there
is therefore no critical behavior, as our perturbative results indicate.
However, it has also been shown that there is a phase transition in the
polynomial model for sufficiently large
model there is a convergent expansion near the
Gaussian point [28], which shows that
the observables are analytical functions of the parameters and that there
is therefore no critical behavior, as our perturbative results indicate.
However, it has also been shown that there is a phase transition in the
polynomial model for sufficiently large
![]() [28], indicating that there
should be a critical line starting somewhere within the critical diagram,
away from the Gaussian point, and extending from there to the critical
point of the Ising model over the arc at infinity. The details regarding
this peculiar situation are currently unknown.
[28], indicating that there
should be a critical line starting somewhere within the critical diagram,
away from the Gaussian point, and extending from there to the critical
point of the Ising model over the arc at infinity. The details regarding
this peculiar situation are currently unknown.
Going back to the cases ![]() , besides the indications that we saw
here, the computer simulations also indicate that the Ising models have
the same triviality behavior of the polynomial models, in the sense that
, besides the indications that we saw
here, the computer simulations also indicate that the Ising models have
the same triviality behavior of the polynomial models, in the sense that
![]() vanishes in the continuum limit. In all these models it
seems that the kinetic term of the action completely dominates the
dynamics, and that the potential terms are not sufficient to change
qualitatively the behavior dictated by the kinetic term. If even making
the coupling parameter
vanishes in the continuum limit. In all these models it
seems that the kinetic term of the action completely dominates the
dynamics, and that the potential terms are not sufficient to change
qualitatively the behavior dictated by the kinetic term. If even making
the coupling parameter ![]() tend to infinity we cannot obtain truly
interacting models, it becomes clear that a deeper structural change of
the models is necessary. This is exactly what one does when one discusses
gauge theories involving vector fields, in which the interactions are
introduced precisely through the kinetic term. There still is, however, a
rather long path to follow before we get to that.
tend to infinity we cannot obtain truly
interacting models, it becomes clear that a deeper structural change of
the models is necessary. This is exactly what one does when one discusses
gauge theories involving vector fields, in which the interactions are
introduced precisely through the kinetic term. There still is, however, a
rather long path to follow before we get to that.