



Next: Fluxogramas
Up: geral
Previous: Conclusões e Perspectivas
Contents
Para a análise dos observáveis ação e número de partículas
apresentamos a seguir os resultados obtidos com os mesmos parâmetros e
a mesma estatística considerados na seção 5.2.1, agora para o modo
(0,0,1,1), nas figuras (A.1) a
(A.8). Em todos os casos os resultados concordam com os
já apresentados no texto.
A figura (A.9) apresenta o comportamento de
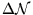 como função do ângulo
como função do ângulo 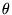 para N crescente, reproduzindo o
mesmo comportamento da figura(5.9).
para N crescente, reproduzindo o
mesmo comportamento da figura(5.9).
Para a análise da energia apresentamos os gráficos
(A.10) a (A.13) para o modo (1,0,0,0),
tipo space-like. Note que (a menos de um fator imaginário devido
aos espaço Euclidiano), o valor absoluto de E0 é positivo nesta
situação. No modo apresentado no texto (0,0,0,1) este valor é negativo
já que ele é um modo tipo time-like).
Figure:
Gráfico do valor esperado da ação como função do número de
partículas na teoria livre, calculados para o modo (0,0,1,1). Os
resultados foram obtidos por simulação estocástica em uma rede com 4
vértices no espaço-tempo quadridimensional.
 |
Figure:
Gráfico do número de partículas obtido por simulações
estocásticas como função do número de partículas analítico na teoria
livre, para o modo (0,0,1,1). Estamos considerando uma rede com 4
vértices no espaço-tempo quadridimensional.
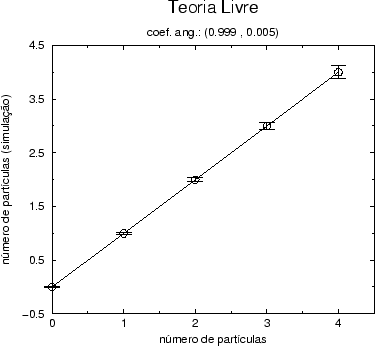 |
Figure:
Gráfico do valor esperado da ação como função do número de
partículas na teoria interagente com 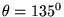 e r=1, calculados
para o modo (0,0,1,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1, calculados
para o modo (0,0,1,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
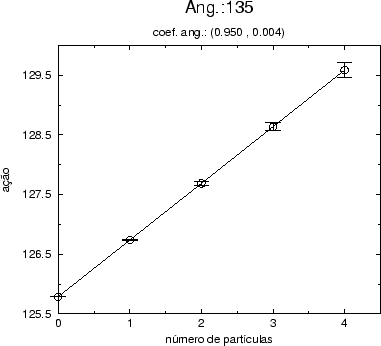 |
Figure:
Gráfico do número de partículas obtido por simulações
estocásticas como função do número de partículas analítico na teoria
interagente com  e r=1, para o modo (0,0,1,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1, para o modo (0,0,1,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
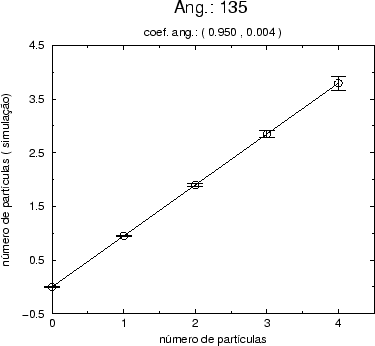 |
Figure:
Gráfico do valor esperado da ação como função do número de
partículas na teoria interagente com  e r=1, calculados
para o modo (0,0,1,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1, calculados
para o modo (0,0,1,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
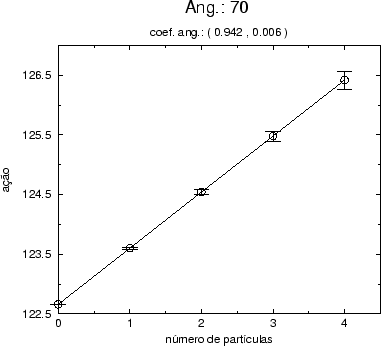 |
Figure:
Gráfico do número de partículas obtido por simulações
estocásticas como função do número de partículas analítico na teoria
interagente com 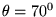 e r=1, para o modo (0,0,1,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1, para o modo (0,0,1,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
 |
Figure:
Gráfico do valor esperado da ação como função do número de
partículas na teoria interagente com  e r=1, calculados
para o modo (0,0,1,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1, calculados
para o modo (0,0,1,1). Os resultados foram obtidos por simulação
estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
 |
Figure:
Gráfico do número de partículas obtido por simulações
estocásticas como função do número de partículas analítico na teoria
interagente com  e r=1, para o modo (0,0,1,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
e r=1, para o modo (0,0,1,1). Estamos
considerando uma rede com 4 vértices no espaço-tempo
quadridimensional.
 |
Figure:
Gráfico do coeficiente angular da escada do número de
partículas
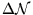 como função do ângulo
como função do ângulo
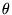 para o modo (0,0,1,1), com d=4 e N=4. Temos aqui um
indicativo de que o número de partículas torna-se inteiro (
para o modo (0,0,1,1), com d=4 e N=4. Temos aqui um
indicativo de que o número de partículas torna-se inteiro (
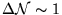 )
nas imediações da linha crítica do modelo
)
nas imediações da linha crítica do modelo
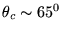 .
.
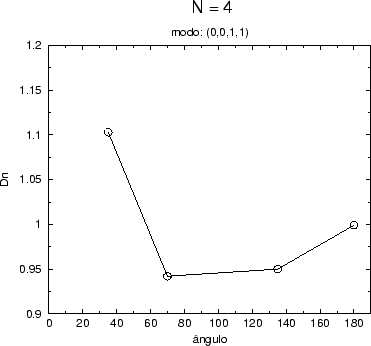 |
Figure:
Gráfico da energia como função do número de partículas na teoria
livre, calculados para o modo (1,0,0,0). Os resultados foram obtidos
por simulação estocástica em uma rede com 4 vértices no espaço-tempo
quadridimensional.
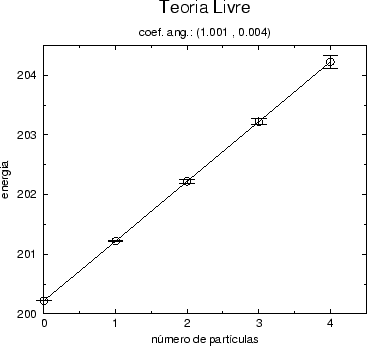 |
Figure:
Gráfico da energia como função do número de partículas na teoria
interagente com  e r=1, calculados para o modo
(1,0,0,0). Os resultados foram obtidos por simulação estocástica em
uma rede com 4 vértices no espaço-tempo quadridimensional.
e r=1, calculados para o modo
(1,0,0,0). Os resultados foram obtidos por simulação estocástica em
uma rede com 4 vértices no espaço-tempo quadridimensional.
 |
Figure:
Gráfico da energia como função do número de partículas na teoria
interagente com  e r=1, calculados para o modo
(1,0,0,0). Os resultados foram obtidos por simulação estocástica em
uma rede com 4 vértices no espaço-tempo quadridimensional.
e r=1, calculados para o modo
(1,0,0,0). Os resultados foram obtidos por simulação estocástica em
uma rede com 4 vértices no espaço-tempo quadridimensional.
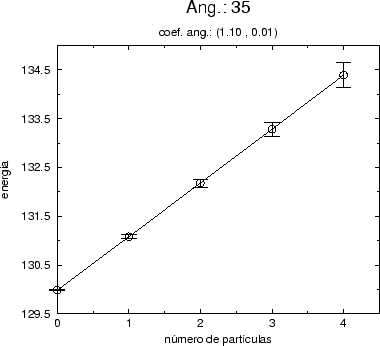 |
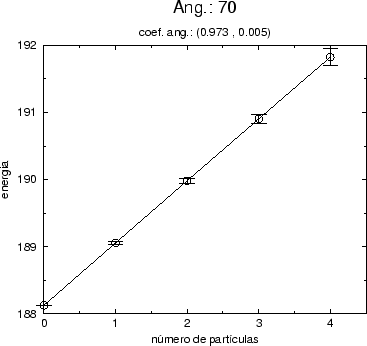
Figure:
Gráfico da energia como função do número de partículas na teoria
interagente com 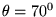 e r=1, calculados para o modo
(1,0,0,0). Os resultados foram obtidos por simulação estocástica em
uma rede com 4 vértices no espaço-tempo quadridimensional.
e r=1, calculados para o modo
(1,0,0,0). Os resultados foram obtidos por simulação estocástica em
uma rede com 4 vértices no espaço-tempo quadridimensional.
 |




Next: Fluxogramas
Up: geral
Previous: Conclusões e Perspectivas
Contents
![]() como função do ângulo
como função do ângulo ![]() para N crescente, reproduzindo o
mesmo comportamento da figura(5.9).
para N crescente, reproduzindo o
mesmo comportamento da figura(5.9).












