Next: Analytic Criterion for Real Up: Fourier Theory on the Previous: Weakening the Convergence Hypothesis
Again we start with an arbitrary integrable DP real function ![]() that has zero average value, with
that has zero average value, with
![]() . Let us now assume
that this function is such that the corresponding Fourier coefficients
. Let us now assume
that this function is such that the corresponding Fourier coefficients
![]() satisfy the condition that
satisfy the condition that
for all real ![]() . What this means is that
. What this means is that ![]() may or may not go to
zero as
may or may not go to
zero as ![]() , may approach a non-zero real number, and may even
diverge to infinity as
, may approach a non-zero real number, and may even
diverge to infinity as ![]() , so long as it does not do so
exponentially fast. This includes therefore not only the sequences of
Fourier coefficients corresponding to all possible convergent Fourier
series, but many sequences that correspond to Fourier series that diverge
almost everywhere. In fact, it even includes sequences of coefficients
that cannot be obtained at all from a real function, such as the sequence
, so long as it does not do so
exponentially fast. This includes therefore not only the sequences of
Fourier coefficients corresponding to all possible convergent Fourier
series, but many sequences that correspond to Fourier series that diverge
almost everywhere. In fact, it even includes sequences of coefficients
that cannot be obtained at all from a real function, such as the sequence
![]() for all
for all ![]() , which is associated to the Dirac delta
``function''
, which is associated to the Dirac delta
``function''
![]() , as shown in [1] and as will be
discussed in Section 5 of this paper. It is therefore a very
weak condition indeed.
, as shown in [1] and as will be
discussed in Section 5 of this paper. It is therefore a very
weak condition indeed.
Before anything else, let us establish a preliminary result, namely that the condition in Equation (3) implies that we also have
for all real powers ![]() . This is just a formalization of the well-known
fact that the negative-exponent real exponential function goes to zero
faster than any positive power goes to infinity, as
. This is just a formalization of the well-known
fact that the negative-exponent real exponential function goes to zero
faster than any positive power goes to infinity, as ![]() . We may
write the function of
. We may
write the function of ![]() on the left-hand side as
on the left-hand side as
Recalling the properties of the logarithm, we now observe that, given an
arbitrary real number ![]() , there is always a sufficiently large value
, there is always a sufficiently large value
![]() of
of ![]() above which
above which ![]() . A simple proof can be found in
Appendix A. Due to this we may write, for all
. A simple proof can be found in
Appendix A. Due to this we may write, for all ![]() ,
,
since the exponential is a monotonically increasing function. If we choose
![]() , which is positive and not zero, we get that, for all
, which is positive and not zero, we get that, for all
![]() ,
,
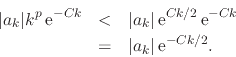
According to our hypothesis about the coefficients ![]() , the
, the
![]() limit of the expression in the right-hand side is zero for
any strictly positive value of
limit of the expression in the right-hand side is zero for
any strictly positive value of ![]() , so that taking the
, so that taking the ![]() limit we establish our preliminary result,
limit we establish our preliminary result,
for all real ![]() and all real
and all real ![]() . If we now construct the complex
power series
. If we now construct the complex
power series ![]() as before, using the coefficients
as before, using the coefficients ![]() , we are in
a position to show that it is absolutely convergent inside the open unit
disk. In order to do this we consider the real power series
, we are in
a position to show that it is absolutely convergent inside the open unit
disk. In order to do this we consider the real power series
![]() of the absolute values of the terms of the series
of the absolute values of the terms of the series
![]() , which we write as
, which we write as
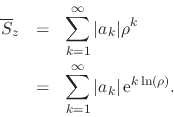
Since ![]() inside the open unit disk, the logarithm shown is strictly
negative, and we may put
inside the open unit disk, the logarithm shown is strictly
negative, and we may put ![]() with real
with real ![]() . We can now see
that, according to our hypothesis about the coefficients
. We can now see
that, according to our hypothesis about the coefficients ![]() , the
terms of this series go to zero exponentially fast as
, the
terms of this series go to zero exponentially fast as ![]() . This
already suffices to establish its convergence, but we may easily make this
more explicit, writing
. This
already suffices to establish its convergence, but we may easily make this
more explicit, writing
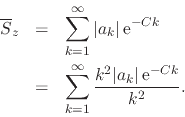
According to our preliminary result in Equation (4) the
numerator shown goes to zero as ![]() , and therefore above a
sufficiently large value
, and therefore above a
sufficiently large value ![]() of
of ![]() it is less that one, so we may
write that
it is less that one, so we may
write that
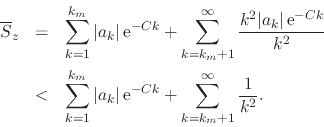
The first term on the right-hand side is a finite sum and therefore is
finite, and the second term can be bounded from above by a convergent
asymptotic integral on ![]() , so that we have
, so that we have
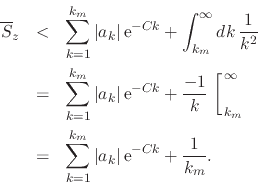
It follows that
![]() , which is a real sum of positive terms,
so that its partial sums form a monotonically increasing sequence, is
bounded from above and is therefore convergent. It then follows that
, which is a real sum of positive terms,
so that its partial sums form a monotonically increasing sequence, is
bounded from above and is therefore convergent. It then follows that
![]() is absolutely convergent and therefore convergent. Since this is
valid for all
is absolutely convergent and therefore convergent. Since this is
valid for all ![]() , we may conclude that
, we may conclude that ![]() converges on the open
unit disk. We may now recover
converges on the open
unit disk. We may now recover ![]() as the
as the ![]() limit of the
real or imaginary part of
limit of the
real or imaginary part of ![]() , as the case may be, almost everywhere on
the unit circle, as was mentioned before and shown in [1].
, as the case may be, almost everywhere on
the unit circle, as was mentioned before and shown in [1].
This provides therefore a very general condition on the Fourier coefficients of the real functions that ensures that the correspondence established in [1] holds. This then ensures that the real functions can be recovered from, and therefore can be represented by, their Fourier coefficients. Note that the condition in Equation (3) can be considered as an even weaker form of the condition discussed in the previous section. We are therefore ready to state our first important conclusion:

Note that, although we formulated this condition in terms of the Fourier
coefficients ![]() of a given DP real function, the fact that
of a given DP real function, the fact that ![]() are the Fourier coefficients of the function has in fact not been used at
all. Therefore, the conclusion is valid for any sequence of coefficients
that satisfies Equation (3), regardless of whether or not
they can be obtained as the Fourier coefficients of some real function.
are the Fourier coefficients of the function has in fact not been used at
all. Therefore, the conclusion is valid for any sequence of coefficients
that satisfies Equation (3), regardless of whether or not
they can be obtained as the Fourier coefficients of some real function.