Analytic Criterion for Real Functions

Finally, let us establish a simple analytic condition over the real functions that ensures that they are representable by their Fourier coefficients. If we assume that $f(\theta)$ is absolutely integrable, so that the integral

$$\frac{1}{\pi} \int_{-\pi}^{\pi}d\theta\, \vert f(\theta)\vert = F$$

exists and is a finite real number $F$, then it follows that we have for the Fourier coefficients, taking as an example the case of the cosine series,

$$\begin{eqnarray*} \vert a_{k}\vert & = & \left\vert \frac{1}{\pi} \int_{-\p... ...\int_{-\pi}^{\pi}d\theta\, \vert f(\theta)\vert \\ & = & F, \end{eqnarray*}$$

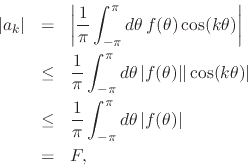
where we used the triangular inequalities. It follows that we have, for all $k\geq 1$,

$$\vert a_{k}\vert \leq F.$$

Since we thus see that the Fourier coefficients of $f(\theta)$ are bounded within the interval $[-F,F]$, for all $k\geq 1$, it follows that they cannot diverge to infinity as $k\to\infty$, and therefore that they satisfy our hypothesis in Equation (3), namely that

$$\lim_{k\to\infty} \vert a_{k}\vert\,{\rm e}^{-Ck} = 0,$$

for all real $C>0$. The same result can be established in a similar way for the case of the sine series, of course. It therefore follows that $f(\theta)$ is representable by its Fourier coefficients.

If we go back to a more general function $f(\theta)$ that has both even and odd parts, since the result holds for both parts, since we may also add a constant term without changing the result, and since we have limited ourselves to Lebesgue-measurable real functions within a compact interval, for which integrability and absolute integrability are one and the same concept, we are ready to state our second important conclusion:

$\parbox{\textwidth}{\bf\boldmath Any integrable real function $f(\th... ...val, regardless of whether or not the corresponding Fourier series converges.}$

It is an interesting observation that this provides an answer to the conjecture proposed in [1], about whether or not there are any integrable real functions such that their sequences of Fourier coefficients $a_{k}$ give rise to complex power series $S_{z}$ which are strongly divergent, that is, that have at least one singular point strictly within the open unit disk. The answer, according to the proof worked out here, is that there are none, as expected.