Discussion and Extensions

In their use of Fourier series for the solution of physical problems, physicists often, and quite successfully, simply ignore convergence issues of the Fourier series involved. With just a bit of common sense and a willingness to accept approximate results, they just plow ahead with their calculations, and that seldom leads them into serious trouble. This is true even if one includes the occasional appearance in these calculations of the Fourier series of singular objects such as Dirac's delta ``function'', since there is usually not much difficulty in interpreting the divergences in physical terms.

The results established here can be viewed as an explanation of this rather remarkable fact. Functions that are useful in physics applications are always at the very least Lebesgue-measurable, and most often at least locally integrable almost everywhere. Extremely pathological functions are not of any use in such circumstances. Therefore, for all real functions of interest in physics applications, there is in effect an underlying analytic structure that firmly anchors all the operations which are performed on the Fourier series, mapping them onto corresponding and much safer operations on the inner-analytic functions within the open unit disk. These operations may include anything from the basic arithmetic operations to integration and differentiation, and so on.

The representation of real functions by their Fourier coefficients, which in physics usually goes by the name of ``representation in momentum space'', often can be interpreted directly in terms of physical concepts. In fact, this alternative representation is frequently found to be the more important and fundamental one. In terms of the mathematical structure that we are dealing with here, it is clear that this state of affairs relates closely to the fact that the analytic structure within the open unit disk is quite clearly the more fundamental aspect of this whole mathematical structure. In the usual physics parlance, that analytic structure is an exact and universal ``regulator'' for all integrable real functions.

It may be possible to further extend the result presented in the previous section. Observe that if the real function $f(\theta)$ is limited and integrable, then its Fourier coefficients $a_{k}$ are also limited, and thus it is obvious that they satisfy the condition in Equation (3), so that they do not diverge exponentially fast with $k$. However, the function does not have to be limited in order for the coefficients to satisfy that condition. The function may diverge to infinity at an isolated point, so long as the asymptotic integral around that point exists. If the function diverges to infinity at a point $\theta_{0}$ in such a way that the integrals

$$\begin{eqnarray*} I_{\ominus} & = & \int_{\theta_{\ominus}}^{\theta_{0}}d\the... ... & = & \int_{\theta_{0}}^{\theta_{\oplus}}d\theta\, f(\theta), \end{eqnarray*}$$

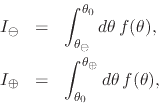
exist and are finite for some $\theta_{\ominus}$ and $\theta_{\oplus}$, with $\theta_{\ominus}<\theta_{0}<\theta_{\oplus}$, and where there are no other hard singularities of $f(\theta)$ within the intervals $[\theta_{\ominus},\theta_{0})$ and $(\theta_{0},\theta_{\oplus}]$, then the function is integrable and thus representable by its Fourier coefficients. One may also have a finite number of such isolated points without disturbing these properties. One may even consider the inclusion of a denumerable infinity of such points, so long as the numerical series resulting from the sum of the contributions of all the singular points to the integral is absolutely convergent, since otherwise the function cannot be considered to be integrable.

Another interesting extension of the results presented in the two previous sections would be one leading of the inclusion in the structure of singular objects which are not real functions, such as extended functions or distributions in the sense of Schwartz [4], represented by their distribution kernels, such as Dirac's delta ``function''. This extension seems to be relatively straightforward, and these objects are routinely dealt with, without too much trouble, in physics applications. These singular objects are also associated to inner analytic functions.

Note that, since the Fourier coefficients of any absolutely integrable real function are necessarily limited, these sequences of coefficients form only a small subset of the set of all the sequences of coefficients that satisfy the condition stated in Equation (3), since many sequences of coefficients which are not limited may satisfy that condition. This shows once again that the condition on the coefficients is in fact very weak. Besides, that condition may be applied to any sequence of real coefficients, whether or not they are the Fourier coefficients of a real function. Therefore, the condition includes much more than just real functions, since there may be many sequences of coefficients $a_{k}$ that satisfy it but that are not obtainable from a real function on the unit circle, as its sequence of Fourier coefficients.

In other words, there are inner analytic functions within the open unit disk that correspond to definite sequences of coefficients $a_{k}$ satisfying our hypothesis, but that are not related to a real function on the unit circle. These inner analytic functions have at least one hard singularity over the unit circle, such as a simple pole, or harder. A hard singularity is defined in [2] as a point at which the limit of the inner-analytic function does not exist, or diverges to infinity. A related gradation in terms of degrees of hardness is also defined there. One important example of this is the inner analytic function associated to the Dirac delta ``function'', which was given in [1]. Given a point $z_{1}$ on the unit circle, the very simple analytic function

$$w_{\delta}(z) = \frac{1}{2\pi} - \frac{1}{\pi}\, \frac{z}{z-z_{1}},$$

which has a simple pole on the unit circle, is an extended inner analytic function, that is, an inner analytic function rotated by the angle $\theta_{1}$ associated to $z_{1}=\exp(\mbox{\boldmath$\imath$}\theta_{1})$ and with the constant shown added to it. This analytic function within the open unit disk is such that the delta ``function'' can be obtained as the limit to the unit circle of its real part,

$$\delta(\theta-\theta_{1}) = \lim_{\rho\to 1} \Re[w_{\delta}(z)],$$

as was shown in [1] with basis on the properties that define the delta ``function''. It would be interesting to further investigate this extension, which would probably include every integrable object which is not a real function. In particular, it would be interesting to investigate whether or not there is a condition such as the condition of absolute integrability which is a sufficient condition, and possibly also a necessary condition, for the representability of such objects by their Fourier coefficients.