Next: Representability by the Fourier Up: Fourier Theory on the Previous: Introduction
Let ![]() be a DP real function that has zero average value, with
be a DP real function that has zero average value, with
![]() . We will assume that
. We will assume that ![]() is an integrable
function, so that its Fourier coefficients
is an integrable
function, so that its Fourier coefficients ![]() and
and ![]() exist, since they are given by
exist, since they are given by
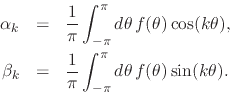
Note that ![]() because
because ![]() is assumed to be a
zero-average function. We will name such coefficients
is assumed to be a
zero-average function. We will name such coefficients ![]() , for
, for
![]() , irrespective of whether
, irrespective of whether ![]() is even or
odd, and thus of whether it gives origin respectively to a cosine or sine
series. Let us assume that the
is even or
odd, and thus of whether it gives origin respectively to a cosine or sine
series. Let us assume that the ![]() coefficients satisfy the following
hypothesis: given a sequence
coefficients satisfy the following
hypothesis: given a sequence ![]() of coefficients, there exists a
positive real function
of coefficients, there exists a
positive real function ![]() with the property that
with the property that
and such that for all ![]()
What this means is that we assume that the ratio of the absolute values of
two consecutive coefficients is bounded from above by a function that
tends to one in the ![]() limit. Note that the
limit. Note that the ![]() limit
of the ratio of coefficients itself may not even exist. Note also that, if
this condition holds for a given DP real function, then it automatically
holds for the corresponding FC real function as well, since both have the
same coefficients and the condition is imposed only on these coefficients.
Following the development described in [1], given
limit
of the ratio of coefficients itself may not even exist. Note also that, if
this condition holds for a given DP real function, then it automatically
holds for the corresponding FC real function as well, since both have the
same coefficients and the condition is imposed only on these coefficients.
Following the development described in [1], given ![]() with such properties we may now construct the two DP trigonometric series
with such properties we may now construct the two DP trigonometric series
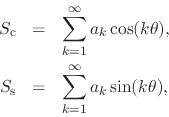
which are the FC series of one another, and then the complex power series
![\begin{eqnarray*}
S_{z}
& = &
\sum_{k=1}^{\infty}
a_{k}\rho^{k}
\left[
\co...
...(k\theta)
\right]
\\
& = &
\sum_{k=1}^{\infty}
a_{k}z^{k},
\end{eqnarray*}](img22.png)
where
![]() , with
, with ![]() , so that
, so that ![]() and
and
![]() are respectively the real and imaginary parts of
are respectively the real and imaginary parts of ![]() for
for
![]() . Note that the condition expressed by
Equations (1) and (2) does not, by
itself, imply the convergence of the series
. Note that the condition expressed by
Equations (1) and (2) does not, by
itself, imply the convergence of the series ![]() and
and ![]() on
the unit circle, since sequences of coefficients
on
the unit circle, since sequences of coefficients ![]() that do not go to
zero as
that do not go to
zero as ![]() may satisfy it. Therefore, many sequences of
coefficients leading to Fourier series that diverge on the unit circle
satisfy that condition. If we now use the ratio criterion to analyze the
convergence of the power series
may satisfy it. Therefore, many sequences of
coefficients leading to Fourier series that diverge on the unit circle
satisfy that condition. If we now use the ratio criterion to analyze the
convergence of the power series ![]() inside the open unit disk, we get
inside the open unit disk, we get
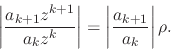
Our hypothesis about the ratio of the ![]() coefficients now leads to
the relation, inside the open unit disk,
coefficients now leads to
the relation, inside the open unit disk,
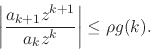
Now, given any value of ![]() , since the limit of
, since the limit of ![]() for
for
![]() is one, it follows that the same limit of
is one, it follows that the same limit of ![]() is
strictly less than one. Therefore, we may conclude that there is a value
is
strictly less than one. Therefore, we may conclude that there is a value
![]() of
of ![]() such that, if
such that, if ![]() , then
, then ![]() , so that the
ratio is less that one, thus implying that we have
, so that the
ratio is less that one, thus implying that we have
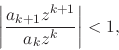
for ![]() . This implies that the ratio criterion is satisfied and
therefore that the series
. This implies that the ratio criterion is satisfied and
therefore that the series ![]() converges at such points. Since this is
true for any
converges at such points. Since this is
true for any ![]() , we may conclude that the power series
, we may conclude that the power series ![]() converges on the open unit disk. Therefore, the series converges to a
complex analytic function
converges on the open unit disk. Therefore, the series converges to a
complex analytic function ![]() there, which is an inner analytic
function according to the definition given in [1].
there, which is an inner analytic
function according to the definition given in [1].
The results established in [1] then imply that ![]() can
now be obtained almost everywhere over the unit circle as the
can
now be obtained almost everywhere over the unit circle as the ![]() limit of the real or imaginary part of
limit of the real or imaginary part of ![]() , as the case may be. Note
that the series
, as the case may be. Note
that the series ![]() , and hence the series
, and hence the series ![]() and
and ![]() ,
may still be divergent over the whole unit circle. This does not affect
the recovery of the real function from its Fourier coefficients in the
manner just described. We have therefore shown that the correspondence
established in [1] holds without the hypothesis that
,
may still be divergent over the whole unit circle. This does not affect
the recovery of the real function from its Fourier coefficients in the
manner just described. We have therefore shown that the correspondence
established in [1] holds without the hypothesis that ![]() and
and ![]() be convergent together on at least at one point of
the unit circle, so long as the Taylor-Fourier coefficients
be convergent together on at least at one point of
the unit circle, so long as the Taylor-Fourier coefficients ![]() satisfy the weaker condition expressed by Equations (1)
and (2).
satisfy the weaker condition expressed by Equations (1)
and (2).