Next: Weakening the Convergence Hypothesis Up: Fourier Theory on the Previous: Fourier Theory on the
In a previous paper [1] we have developed a correspondence
between, on one side, the Fourier series and Fourier coefficients of real
functions on the interval ![]() and, on the other side, a complex
analytic structure within the open unit disk, consisting of a set of inner
analytic functions and their complex Taylor series. The reader is referred
to that paper for the definition of many of the concepts and notations
used in this one. In many cases this correspondence leads to the
formulation of expressions involving modified trigonometric series that
can converge very fast to a given real function, even when the Fourier
series of that function diverges or converges very slowly, as shown
in [2].
and, on the other side, a complex
analytic structure within the open unit disk, consisting of a set of inner
analytic functions and their complex Taylor series. The reader is referred
to that paper for the definition of many of the concepts and notations
used in this one. In many cases this correspondence leads to the
formulation of expressions involving modified trigonometric series that
can converge very fast to a given real function, even when the Fourier
series of that function diverges or converges very slowly, as shown
in [2].
In order to establish the correspondence described above,
in [1] we assumed that the Definite Parity (DP) real functions
![]() under examination are such that their Fourier series and the
corresponding Fourier Conjugate (FC) series converge together on at least
one point on the interval
under examination are such that their Fourier series and the
corresponding Fourier Conjugate (FC) series converge together on at least
one point on the interval ![]() , a domain which, in the context of
the correspondence to be established, is mapped onto the unit circle of
the complex plane. In this paper we will show that one can relax that
hypothesis, replacing it by a much weaker one.
, a domain which, in the context of
the correspondence to be established, is mapped onto the unit circle of
the complex plane. In this paper we will show that one can relax that
hypothesis, replacing it by a much weaker one.
Following the development in [1], we will deal here only with
real functions that have definite parity properties, which we will call
Definite Parity real functions or DP real functions for short. Since any
real function ![]() in the interval
in the interval ![]() , without any
restriction, can be separated into even and odd parts,
, without any
restriction, can be separated into even and odd parts,
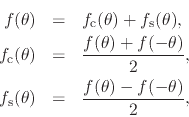
where
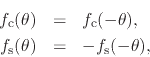
we can restrict the discussion to Definite Parity (DP) real functions
without any loss of generality. This condition implies that the
corresponding inner analytic function ![]() has the property that it
reduces to a real function on the interval
has the property that it
reduces to a real function on the interval ![]() of the real axis, as
discussed in [1]. For simplicity, we will also assume that
of the real axis, as
discussed in [1]. For simplicity, we will also assume that
![]() is a zero-average function, since adding a constant function
to
is a zero-average function, since adding a constant function
to ![]() is a trivial operation that does not significantly affect
the issues under discussion here. This condition implies that the
corresponding inner analytic function
is a trivial operation that does not significantly affect
the issues under discussion here. This condition implies that the
corresponding inner analytic function ![]() has the property that
has the property that
![]() , as discussed in [1].
, as discussed in [1].
In Subsection ![]() of [1] we have shown that, if there is any
singularity of an analytic function
of [1] we have shown that, if there is any
singularity of an analytic function ![]() inside the open unit disk, then
the sequence of Taylor-Fourier coefficients of its Taylor series diverges
to infinity exponentially fast on the unit circle, as a function of the
series index. In this paper we will discuss the converse of this
statement. We will show here that the mere absence of an
exponentially-fast divergence of the sequence of Fourier coefficients on
the unit circle is enough to ensure the convergence of the corresponding
complex power series inside the open unit disk, thus leading to the
definition of a corresponding inner analytic function.
inside the open unit disk, then
the sequence of Taylor-Fourier coefficients of its Taylor series diverges
to infinity exponentially fast on the unit circle, as a function of the
series index. In this paper we will discuss the converse of this
statement. We will show here that the mere absence of an
exponentially-fast divergence of the sequence of Fourier coefficients on
the unit circle is enough to ensure the convergence of the corresponding
complex power series inside the open unit disk, thus leading to the
definition of a corresponding inner analytic function.
A note about the concept of integrability of real functions is in order at this point. What we mean by integrability in this paper is integrability in the sense of Lebesgue, with the use of the usual Lebesgue measure. We will assume that all the real functions at issue here are measurable in the Lebesgue measure. Therefore whenever we speak of real functions, it should be understood that we mean Lebesgue-measurable real functions. We will use the following result from the theory of measure and integration: for real functions defined within a compact interval, which are Lebesgue measurable, integrability and absolute integrability are equivalent conditions [3]. Therefore we will use the concepts of integrability and of absolute integrability interchangeably.