A Property of the Logarithm

Let us show that the logarithm has the property that given an arbitrary real number $A>0$, there is always a sufficiently large value $k_{m}$ of the integer $k$ above which $\ln(k)<Ak$. We simply promote $k$ to a continuous real variable $x>0$ and consider the function

$$h(x) = Ax-\ln(x).$$

Is is quite clear that this function diverges to positive infinity as $x\to 0$. If we calculate the first and second derivatives of $h(x)$ we get

$$\begin{eqnarray*} h'(x) & = & A-\frac{1}{x}, \\ h''(x) & = & \frac{1}{x^{2}}. \end{eqnarray*}$$

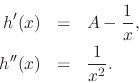
It is now clear that there is a single critical point where the first derivative is zero, that is where $h'(x_{0})=0$, given by $x_{0}=1/A$. At this point we have for the second derivative

$$h''(x_{0}) = A^{2},$$

which is positive, implying that the critical point is a local minimum. Since there is no other minimum, maximum or inflection point, it becomes clear that the function must decrease from positive infinity as $x$ increases from zero, go through the point of minimum at $x_{0}$, and then increase without limit as $x\to\infty$. At this point of minimum we have for the function itself,

$$h(x_{0}) = 1+\ln(A).$$

It follows that, if $h(x_{0})>0$, then we must have $h(x)>0$ for all $x>0$. This corresponds to $A>1/e$. On the other hand, if $h(x_{0})\leq 0$, then there are two solutions $x_{1}$ and $x_{2}$ of the equation $h(x)=0$, that coincide if $h(x_{0})=0$. This corresponds to $0<A\leq 1/e$. In this case the function is positive within the interval $(0,x_{1})$, negative within $(x_{1},x_{2})$ and positive for $x>x_{2}$.

Therefore, for all possible values of $A$ there is a value $x_{m}$ of $x$, either $x_{m}=0$ or $x_{m}=x_{2}$, such that for $x>x_{m}$ the function $h(x)$ is positive, and therefore

$$Ax > \ln(x).$$

Translating the statement back in terms of $k$, we have that given any real number $A>0$, there is a minimum value $k_{m}$ of the integer $k$ such that $Ak>\ln(k)$. Thus the required statement is established.