Non-Integrable Real Functions on Differentiable Curves

In this section we will show how one can generalize the proof of existence of the Dirichlet problem on the unit disk, given by Theorem 2 in Section 3, to the case in which we have, as the boundary condition, non-integrable real functions $f_{b}(\lambda)$ defined on boundaries given by differentiable curves $C_{b}$ on the plane. We will be able to do this if the non-integrable real functions, despite being non-integrable over the whole curves $C_{b}$, are however locally integrable almost everywhere on those curves, and if, in addition to this, the non-integrable hard singularities of the inner analytic functions involved have finite degrees of hardness. The definition of the concept of local integrability almost everywhere is similar to that given for the unit circle by Definition 2, in Section 3. In our case here the precise definition of local integrability almost everywhere is as follows.

Definition 4   : A real function $f(\lambda)$ is locally integrable almost everywhere on the curve $C$ described by the arc-length parameter $\lambda$ if it is integrable on every closed interval $[\lambda_{\ominus},\lambda_{\oplus}]$ contained within that domain, that does not contain any of the points where the function has non-integrable hard singularities, of which there is a finite number.

The proof will follow the general lines of the one given for integrable real functions in Section 5, with the difference that, since the real functions $f_{b}(\lambda)$ are assumed to be non-integrable on $C_{b}$, but locally integrable almost everywhere there, instead of showing that the corresponding functions $f_{a}(\theta)$ on the unit circle $C_{a}$ are integrable there, we will show that they are locally integrable almost everywhere there. In addition to this, instead of using the result for integrable real function on the unit circle, which was given by Theorem 1 in Section 2, we will use the corresponding result for non-integrable real functions which are locally integrable almost everywhere on the unit circle, which was given by Theorem 2 in Section 3. Since that result depends also on the non-integrable hard singularities of the real functions having finite degrees of hardness, we will also show that the hypothesis that the functions $f_{b}(\lambda)$ have this property implies that the corresponding functions $f_{a}(\theta)$ have the same property as well. In order to do this we will use the technique of piecewise integration which was introduced and employed in [#!CAoRFIV!#], where it played a crucial role.

We will start by showing the following preliminary fact about a real function $f_{a}(\theta)$ defined from a real function $f_{b}(\lambda)$ which is locally integrable almost everywhere on $C_{b}$, and which has non-integrable hard singularities at the finite set of points $z_{b,j}$, for $j\in\{1,\ldots,M\}$.

Lemma 3   : Given a real function $f_{b}(\lambda)$ which is integrable on a given closed interval $I_{b}$ on $C_{b}$, it follows that the corresponding function $f_{a}(\theta)$ defined on the unit circle $C_{a}$ by $f_{a}(\theta)=f_{b}(\lambda)$ is integrable on the corresponding closed interval $I_{a}$ on $C_{a}$, which is mapped from $I_{b}$ by the inverse conformal transformation $\gamma^{(-1)}(z_{b})$.

Since $f_{b}(\lambda)$ is integrable on $I_{b}$ we have that

$$\int_{I_{b}}\vert d\lambda\vert\, \vert f_{b}(\lambda)\vert$$ (37)

exists and is finite. If we now consider the integral

$$\int_{I_{a}}\vert d\theta\vert\, \vert f_{a}(\theta)\vert,$$ (38)

and transform variables from $\theta$ to $\lambda$, recalling that $f_{a}(\theta)=f_{b}(\lambda)$, we get

$$\int_{I_{a}}\vert d\theta\vert\, \vert f_{a}(\theta)\vert ... ...ac{d\theta}{d\lambda} \right\vert \vert f_{b}(\lambda)\vert.$$ (39)

The absolute value of the derivative shown exists and is finite on $I_{b}$, given that

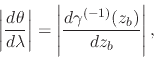$$\left\vert \frac{d\theta}{d\lambda} \right\vert = \left\vert \frac{d\gamma^{(-1)}(z_{b})}{dz_{b}} \right\vert,$$ (40)

where $\gamma^{(-1)}(z_{b})$ is analytic on $C_{b}$ and therefore differentiable there. We also have that $f_{b}(\lambda)$ is integrable on $I_{b}$. It follows that, since the integrand in the right-hand side of Equation (39) is the product of a limited real function with an integrable real function, and therefore is itself an integrable real function, the integral in Equation (39) exists and is finite, thus implying that $f_{a}(\theta)$ is integrable on the closed interval $I_{a}$. This establishes Lemma 3.

As an immediate consequence of this preliminary result, under the conditions that we have here, the hypothesis that $f_{b}(\lambda)$ is locally integrable almost everywhere on $C_{b}$, with the exclusion of the finite set of points $z_{b,j}$, implies that $f_{a}(\theta)$ is locally integrable almost everywhere on $C_{a}$, with the exclusion of the corresponding finite set of points $z_{a,j}$.

We must now discuss the issue of the degrees of hardness of the non-integrable hard singularities of the function $f_{a}(\theta)$ on $C_{a}$. Since by hypothesis $f_{b}(\lambda)$ has non-integrable hard singularities at the points $z_{b,j}$, it clearly follows that $f_{a}(\theta)$ also has hard singularities at the corresponding points $z_{a,j}$, which may be non-integrable ones. In order to discuss their degrees of hardness we will use the technique of piecewise integration, that is, we will consider sectional integrals of $f_{a}(\theta)$ on closed intervals contained within a neighborhood of the point $z_{a,j}$ where it has a single isolated hard singularity. Let us show the following preliminary fact about a real function $f_{a}(\theta)$ defined from a real function $f_{b}(\lambda)$ which is locally integrable almost everywhere on $C_{b}$, and which has non-integrable hard singularities with finite degrees of hardness at the finite set of points $z_{b,j}$.

Lemma 4   : Given a real function $f_{b}(\lambda)$ which has an isolated non-integrable hard singularity with finite degree of hardness at a point $z_{b,j}$ on $C_{b}$, it follows that the corresponding function $f_{a}(\theta)$ defined on the unit circle $C_{a}$ by $f_{a}(\theta)=f_{b}(\lambda)$ has an isolated non-integrable hard singularity with finite degree of hardness at the corresponding point $z_{a,j}$ on $C_{a}$.

Since the real functions must diverge to infinity at non-integrable hard singular points, the fact that $f_{a}(\theta)$ has an isolated hard singularity on $z_{a,j}$ is immediate. Since these singularities are all isolated from each other, there is on $C_{b}$ a neighborhood of the point $z_{b,j}$ within which there are no other non-integrable hard singularities of $f_{b}(\lambda)$. Since the conformal mapping is continuous, it follows that there is on $C_{a}$ a neighborhood of the corresponding point $z_{a,j}$ within which there are no other hard singularities of $f_{a}(\theta)$. Given that the point $z_{a,j}$ corresponds to the angle $\theta_{j}$, let the closed interval $[\theta_{\ominus,j},\theta_{\oplus,j}]$ contain the point $z_{a,j}$ and be contained in this neighborhood, so that we have

$$\theta_{\ominus,j}<\theta_{j}<\theta_{\oplus,j},$$ (41)

where the sole hard singularity of $f_{a}(\theta)$ which is contained within this interval is the one at the point $\theta_{j}$. Let us now consider a pair of closed intervals contained within this neighborhood, one to the left and one to the right of the point $\theta_{j}$, so that we have

$$I_{\ominus,j} = [\theta_{\ominus,j},\theta_{j}-\varepsilon_{\ominus,j}],$$

$$I_{\oplus,j} = [\theta_{j}+\varepsilon_{\oplus,j},\theta_{\oplus,j}],$$ (42)

where $\varepsilon_{\ominus,j}$ and $\varepsilon_{\oplus,j}$ are two sufficiently small positive real numbers, so that we also have

$$\theta_{\ominus,j} < \theta_{j}-\varepsilon_{\ominus,j},$$

$$\theta_{j}+\varepsilon_{\oplus,j} < \theta_{\oplus,j}.$$ (43)

Let us now consider sectional primitives of the real function $f_{a}(\theta)$ on these two intervals. Since the singularity of $f_{a}(\theta)$ at $\theta_{j}$ may not be integrable, we cannot integrate across the singularity, but we may integrate within these two lateral closed intervals, thus defining two sectional primitives of $f_{a}(\theta)$, one to the left and another one to the right of $\theta_{j}$,

$$f_{a,\ominus}^{-1\prime}(\theta) = \int_{\theta_{0,\ominus,j}}^{\theta} d\theta_{\ominus}\, f_{a}(\theta_{\ominus}),$$

$$f_{a,\oplus}^{-1\prime}(\theta) = \int_{\theta_{0,\oplus,j}}^{\theta} d\theta_{\oplus}\, f_{a}(\theta_{\oplus}),$$ (44)

where $f_{a}^{-1\prime}(\theta)$ is the notation for a primitive of $f_{a}(\theta)$ with respect to $\theta$, where $\theta_{0,\ominus,j}$ and $\theta_{0,\oplus,j}$ are two arbitrary reference points, one within each of the two lateral closed intervals, and where we have

$$<tex2html_comment_mark>\renewedcommand{arraystretch}{2.0} ... ... \theta_{0,\oplus,j} & \leq & \theta_{\oplus,j}. \end{array}$$

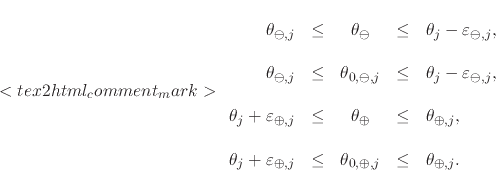If we change variables from $\theta$ to $\lambda$ on the two sectional integrals in Equation (44), we get

$$f_{a,\ominus}^{-1\prime}(\theta) = \int_{\lambda_{0,\ominus,j}}^{\lambda} d\lambda_{\ominus}\, \frac{d\theta}{d\lambda}(\lambda_{\ominus})\, f_{b}(\lambda_{\ominus}),$$

$$f_{a,\oplus}^{-1\prime}(\theta) = \int_{\lambda_{0,\oplus,j}}^{\lambda} d\lambda_{\oplus}\, \frac{d\theta}{d\lambda}(\lambda_{\oplus})\, f_{b}(\lambda_{\oplus}),$$ (45)

where $\lambda_{0,\ominus,j}$ and $\lambda_{0,\oplus,j}$ are the reference points on $C_{b}$ corresponding respectively to $\theta_{0,\ominus,j}$ and $\theta_{0,\oplus,j}$. Since the derivative $d\theta/d\lambda$ which appears in these integrals is finite everywhere on $C_{b}$, and therefore limited, due to the fact that the inverse conformal transformation $\gamma^{(-1)}(z_{b})$ is analytic and hence differentiable on the curve $C_{b}$, it follows that there are two real numbers $R_{m}$ and $R_{M}$ such that

$$R_{m} \leq \frac{d\theta}{d\lambda}(\lambda) \leq R_{M}$$ (46)

everywhere on $C_{b}$. Note that, since the conformal transformation, besides being continuous and differentiable, is also invertible on $C_{b}$, the derivative above cannot change sign and thus cannot be zero. Therefore, the two bounds $R_{m}$ and $R_{M}$ may be chose to have the same sign. By exchanging the derivative by these extreme values we can obtain upper and lower bounds for the sectional integrals, and therefore we get for the sectional primitives in Equation (46),

$$<tex2html_comment_mark>\renewedcommand{arraystretch}{2.0} ... ...da} d\lambda_{\oplus}\, f_{b}(\lambda_{\oplus}). \end{array}$$

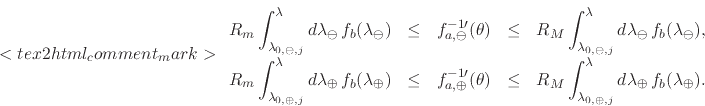We now recognize the integrals that appear in these expressions as the sectional primitives of the function $f_{b}(\lambda)$, so that we get

$$<tex2html_comment_mark>\renewedcommand{arraystretch}{2.0} ... ...\leq & R_{M}\, f_{b,\oplus}^{-1\prime}(\lambda). \end{array}$$

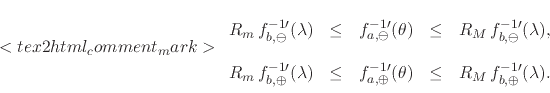These expressions are true so long as $\varepsilon_{\ominus,j}$ and $\varepsilon_{\oplus,j}$, as well as the corresponding quantities $\delta_{\ominus,j}$ and $\delta_{\oplus,j}$ on $C_{b}$, are not zero, but since the singularities at $z_{b,j}$ are non-integrable hard ones, we cannot take the limit in which these quantities tend to zero. Note that, since $R_{m}$ and $R_{M}$ have the same sign, if the sectional primitives of the function $f_{b}(\lambda)$ diverge to infinity in this limit, then so do the sectional primitives of the function $f_{a}(\theta)$. Therefore, we may conclude that the hard singularity of $f_{a}(\theta)$ is also a non-integrable one. Since we may take further sectional integrals of these expressions, without affecting the inequalities, it is immediately apparent that, after a total of $n$ successive piecewise integrations, we get for the $n^{\rm th}$ sectional primitives

$$<tex2html_comment_mark>\renewedcommand{arraystretch}{2.0} ... ...\leq & R_{M}\, f_{b,\oplus}^{-n\prime}(\lambda). \end{array}$$

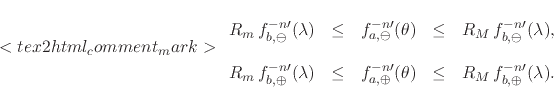Since the non-integrable hard singularity of $f_{b}(\lambda)$ at the point $\lambda_{j}$ which corresponds to $\theta_{j}$ has a finite degree of hardness, according to the definition of the degrees of hardness, which was given in [#!CAoRFI!#] and discussed in detail for the case of real functions in [#!CAoRFIV!#], there is a value of $n$ such that the limit in which $\delta_{\ominus,j}\to 0$ and $\delta_{\oplus,j}\to 0$ can be taken for the sectional primitives $f_{b,\ominus}^{-n\prime}(\lambda)$ and $f_{b,\oplus}^{-n\prime}(\lambda)$, thus implying that the $n^{\rm th}$ piecewise primitive $f_{b}^{-n\prime}(\lambda)$ of $f_{b}(\lambda)$ is an integrable real function on the whole interval $[\lambda_{\ominus,j},\lambda_{\oplus,j}]$ that corresponds to $[\theta_{\ominus,j},\theta_{\oplus,j}]$, with a borderline hard singularity, with degree of hardness zero, at the point $\lambda_{j}$. It follows from the inequalities, therefore, that the corresponding limit in which $\varepsilon_{\ominus,j}\to 0$ and $\varepsilon_{\oplus,j}\to 0$ can be taken for the functions $f_{a,\ominus}^{-n\prime}(\theta)$ and $f_{a,\oplus}^{-n\prime}(\theta)$, thus implying that the $n^{\rm th}$ piecewise primitive $f_{a}^{-n\prime}(\theta)$ of $f_{a}(\theta)$ is also an integrable real function on the whole interval $[\theta_{\ominus,j},\theta_{\oplus,j}]$, with a borderline hard singularity, with degree of hardness zero, at $\theta_{j}$. Therefore, the non-integrable hard singularity of $f_{a}(\theta)$ at $\theta_{j}$ has a finite degree of hardness, to wit the same degree of hardness $n$ of the corresponding non-integrable hard singularity of $f_{b}(\lambda)$ at $\lambda_{j}$. This establishes Lemma 4.

We have therefore established that, so long as $f_{b}(\lambda)$ is locally integrable almost everywhere on $C_{b}$, and so long as its non-integrable hard singularities have finite degrees of hardness, these same two facts are true for $f_{a}(\theta)$ on $C_{a}$. Since we thus see that the necessary properties of the real functions are preserved by the conformal transformation, we are therefore in a position to use the result of Theorem 2 in Section 3 in order to extend the existence theorem of the Dirichlet problem to non-integrable real functions which are, however, integrable almost everywhere on $C_{b}$, still for the case of differentiable curves.

In this section, using once again the results from the previous sections, we will establish the following theorem.

Theorem 5   : Given a differentiable simple closed curve $C$ of finite total length on the complex plane $z=x+\mbox{\boldmath$\imath$}y$, given the invertible conformal transformation $\gamma(z)$ whose derivative has no zeros on the closed unit disk, that maps it from the unit circle, and given a real function $f(\lambda)$ on that curve, that satisfies the list of conditions described below, there is a solution $u(x,y)$ of the Dirichlet problem of the Laplace equation within the interior of that curve, that assumes the given values $f(\lambda)$ almost everywhere at the curve.

Proof 5.1   :

Similarly to what was done in the two previous cases, in Sections 5 and 6, the proof consists of using the conformal transformation between the closed unit disk and the union of the curve $C$ with its interior, which according to the analysis in Section 4 always exists, to map the given boundary condition on $C$ onto a corresponding boundary condition on the unit circle, then using the proof of existence established before by Theorem 2 in Section 3 for the closed unit disk to establish the existence of the solution of the corresponding Dirichlet problem on that disk, and finally using once more the conformal transformation to map the resulting solution back to $C$ and its interior, thus obtaining the solution of the original Dirichlet problem. The list of conditions on the real functions is now the following.

1. The real function $f(\lambda)$ is locally integrable almost everywhere on $C$, including the cases in which this function is globally integrable there.

2. The number of hard singularities on the unit circle of the corresponding inner analytic function $w(z)$ on the unit disk is finite.

3. The hard singularities of the corresponding inner analytic function $w(z)$ have finite degrees of hardness.

The rest of the proof is identical to that of the two previous cases, in Sections 5 and 6. Therefore, once again we may conclude that, due to the existence theorem of the Dirichlet problem on the unit disk of the plane $z_{a}$, which in this case was established by Theorem 2 in Section 3, we know that there is an inner analytic function $w_{a}(z_{a})$ such that its real part $u_{a}(\rho,\theta)$ is harmonic within the open unit disk and satisfies $u_{a}(1,\theta)=f_{a}(\theta)$ almost everywhere at the boundary $C_{a}$. Just as before, we get on the $z_{b}$ plane the complex function $w_{b}(z_{b})$ which is analytic in the interior of the curve $C_{b}$. Therefore, the real part $u_{b}(x,y)$ of $w_{b}(z_{b})$ is harmonic and thus satisfies

$$\nabla^{2}u_{b}(x,y) = 0$$ (47)

in the interior of $C_{b}$, while we also have that

$$u_{b}(x,y)=f_{b}(\lambda),$$ (48)

almost everywhere on $C_{b}$. This establishes the existence, by construction, of the solution of the Dirichlet problem on the $z_{b}$ plane, under our current hypotheses. This completes the proof of Theorem 5.

In this way we have generalized the proof of existence of the Dirichlet problem from the unit circle to all differentiable simple closed curves with finite total lengths on the plane, for boundary conditions given by non-integrable real functions which are locally integrable almost everywhere and have at most a finite set of hard singular points.