Next: Integrable Real Functions on Up: Complex Analysis of Real Previous: Conformal Transformations to Other
In this section we will show how one can generalize the proof of existence of the solution of the Dirichlet problem on the unit disk, given by Theorem 1 in Section 2, to the case in which we have, as the boundary condition, integrable real functions defined on boundaries given by differentiable curves on the plane. In order to do this, the first thing we must do here is to establish the precise definition of the Dirichlet problem in this case.
Given a simple closed curve ![]() on the complex plane, described by a real
arc-length parameter
on the complex plane, described by a real
arc-length parameter ![]() , and a real function
, and a real function ![]() defined
on it, the existence problem of the Dirichlet boundary value problem of
the Laplace equation on this curve and its interior is to show that a
function
defined
on it, the existence problem of the Dirichlet boundary value problem of
the Laplace equation on this curve and its interior is to show that a
function ![]() exists such that it satisfies
exists such that it satisfies
| (20) |
within the interior of ![]() , and such that it also satisfies
, and such that it also satisfies
| (21) |
for
![]() on
on ![]() , thus corresponding to
, thus corresponding to ![]() , almost everywhere
over that curve.
, almost everywhere
over that curve.
Therefore, using the notation established in Section 4, let
![]() be a differentiable simple closed curve on the complex
be a differentiable simple closed curve on the complex ![]() plane, with finite total length, and let us assume that a Dirichlet
boundary value problem for the Laplace equation is given on the region
whose boundary is the curve
plane, with finite total length, and let us assume that a Dirichlet
boundary value problem for the Laplace equation is given on the region
whose boundary is the curve ![]() , that is, let there be given also an
integrable real function
, that is, let there be given also an
integrable real function
![]() on
on ![]() , that is, a function
such that the integral
, that is, a function
such that the integral
| (22) |
exists and is finite. The problem is then to establish the existence of a
function ![]() that satisfies
that satisfies
![]() in the
interior of the curve
in the
interior of the curve ![]() and that assumes the values
and that assumes the values
![]() almost everywhere over that curve. In order to do this using the conformal
transformation
almost everywhere over that curve. In order to do this using the conformal
transformation ![]() from the complex plane
from the complex plane ![]() to the complex
plane
to the complex
plane ![]() , we start by constructing a corresponding Dirichlet problem
on the unit disk of the
, we start by constructing a corresponding Dirichlet problem
on the unit disk of the ![]() plane, using the mapping between
plane, using the mapping between ![]() and
and ![]() provided by the conformal transformation
provided by the conformal transformation ![]() and
its inverse
and
its inverse
![]() . We define a corresponding real
function
. We define a corresponding real
function ![]() on the unit circle
on the unit circle ![]() by simply transferring
the values of
by simply transferring
the values of
![]() through the use of the conformal mapping
from point to point,
through the use of the conformal mapping
from point to point,
| (23) |
where ![]() describes a point on
describes a point on ![]() given by the complex number
given by the complex number
![]() ,
, ![]() describes the corresponding point on
describes the corresponding point on ![]() given by
the complex number
given by
the complex number
![]() , and
, and ![]() is the induced
real transformation, so that we have that
is the induced
real transformation, so that we have that
![]() and that
and that
![]() . We will start by establishing the following
preliminary fact about the real function
. We will start by establishing the following
preliminary fact about the real function ![]() defined as above
from an integrable real function
defined as above
from an integrable real function
![]() .
.
Given that
![]() is integrable on
is integrable on ![]() , we must show that
, we must show that
![]() defined by the composition of
defined by the composition of
![]() with
with
![]() , is also integrable, that is, it is integrable on
, is also integrable, that is, it is integrable on ![]() .
Since all real functions under discussion here are assumed to be
Lebesgue-measurable, and since for such measurable functions defined on
compact domains integrability and absolute integrability are equivalent
conditions [#!RARudin!#,#!RARoyden!#], given that
.
Since all real functions under discussion here are assumed to be
Lebesgue-measurable, and since for such measurable functions defined on
compact domains integrability and absolute integrability are equivalent
conditions [#!RARudin!#,#!RARoyden!#], given that
![]() is
integrable on
is
integrable on ![]() we have that the integral
we have that the integral
| (24) |
exists and is finite. We must now show that the integral
exists and is finite, which is equivalent to the statement that
![]() is integrable on
is integrable on ![]() . Changing variables on this
integral from
. Changing variables on this
integral from ![]() to
to ![]() , and using the fact that by definition
we have that
, and using the fact that by definition
we have that
![]() , we obtain
, we obtain
Since
![]() is integrable on
is integrable on ![]() , and since the absolute
value of the derivative shown exists and is finite, given that we have
, and since the absolute
value of the derivative shown exists and is finite, given that we have
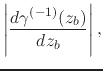 |
(27) |
where
![]() is analytic on
is analytic on ![]() and therefore
differentiable there, it follows that the absolute value of the derivative
which appears in the integrand on the right-hand side of
Equation (26) is a limited real function on
and therefore
differentiable there, it follows that the absolute value of the derivative
which appears in the integrand on the right-hand side of
Equation (26) is a limited real function on ![]() . Since
. Since
![]() is integrable on
is integrable on ![]() , from this it follows that the
whole integrand of the integral on the right-hand side of
Equation (26), which is the product of a limited real
function with an integrable real function, is itself an integrable real
function on
, from this it follows that the
whole integrand of the integral on the right-hand side of
Equation (26), which is the product of a limited real
function with an integrable real function, is itself an integrable real
function on ![]() , so that we may conclude that the integral in
Equation (25) exists and is finite, and therefore that
, so that we may conclude that the integral in
Equation (25) exists and is finite, and therefore that
![]() is an integrable real function on
is an integrable real function on ![]() . This
establishes Lemma 1.
. This
establishes Lemma 1.
In this section, using the results from the previous sections, we will establish the following theorem.
The proof consists of using the conformal transformation between the
closed unit disk and the union of the curve ![]() with its interior, a
transformation which according to the analysis in Section 4
always exists, to map the given boundary condition on
with its interior, a
transformation which according to the analysis in Section 4
always exists, to map the given boundary condition on ![]() onto a
corresponding boundary condition on the unit circle, then using the proof
of existence established before by Theorem 1 in
Section 2 for the closed unit disk to establish the existence of
the solution of the corresponding Dirichlet problem on that disk, and
finally using once more the conformal transformation to map the resulting
solution back to
onto a
corresponding boundary condition on the unit circle, then using the proof
of existence established before by Theorem 1 in
Section 2 for the closed unit disk to establish the existence of
the solution of the corresponding Dirichlet problem on that disk, and
finally using once more the conformal transformation to map the resulting
solution back to ![]() and its interior, showing in the process that one
obtains in this way the solution of the Dirichlet problem there. The list
of conditions on the real functions is now the following.
and its interior, showing in the process that one
obtains in this way the solution of the Dirichlet problem there. The list
of conditions on the real functions is now the following.
According to the preliminary result established in Lemma 1, if
the real function
![]() satisfies these conditions on
satisfies these conditions on ![]() ,
then
,
then ![]() is an integrable real function on
is an integrable real function on ![]() . Therefore,
due to the existence theorem of the Dirichlet problem on the unit disk of
the plane
. Therefore,
due to the existence theorem of the Dirichlet problem on the unit disk of
the plane ![]() , which was established by Theorem 1 in
Section 2, we know that there is an inner analytic function
, which was established by Theorem 1 in
Section 2, we know that there is an inner analytic function
![]() such that its real part
such that its real part
![]() is harmonic
within the open unit disk and also satisfies
is harmonic
within the open unit disk and also satisfies
![]() almost everywhere at the boundary
almost everywhere at the boundary ![]() .
Now, by composing
.
Now, by composing ![]() with the inverse conformal transformation
with the inverse conformal transformation
![]() we get on the
we get on the ![]() plane the complex function
plane the complex function
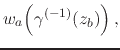 |
(28) |
which corresponds to simply transferring back the values of
![]() , by the use of the conformal mapping from point to point,
while we also have, of course, the corresponding inverse real
transformation at the boundary,
, by the use of the conformal mapping from point to point,
while we also have, of course, the corresponding inverse real
transformation at the boundary,
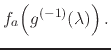 |
(29) |
Given that the composition of two analytic functions is also analytic, in
their chained domain of analyticity, and since
![]() is
analytic in the interior of the curve
is
analytic in the interior of the curve ![]() , and also since
, and also since
![]() is analytic in the interior of the curve
is analytic in the interior of the curve ![]() , we
conclude that
, we
conclude that ![]() is analytic in the interior of the curve
is analytic in the interior of the curve
![]() . Therefore, the real part
. Therefore, the real part ![]() of
of ![]() is
harmonic and thus satisfies
is
harmonic and thus satisfies
| (30) |
in the interior of ![]() , while by construction the fact that we have
, while by construction the fact that we have
![]() for the points given by
for the points given by
![]() almost everywhere on
almost everywhere on ![]() , where
, where ![]() ,
implies that we also have
,
implies that we also have
| (31) |
for the corresponding points given by
![]() almost everywhere on
almost everywhere on
![]() , and which thus correspond to
, and which thus correspond to ![]() . This establishes the
existence, by construction, of the solution of the Dirichlet problem on
the
. This establishes the
existence, by construction, of the solution of the Dirichlet problem on
the ![]() plane, under our current hypotheses. This completes the proof
of Theorem 3.
plane, under our current hypotheses. This completes the proof
of Theorem 3.
In this way we have generalized the proof of existence of the Dirichlet problem from the unit circle to all differentiable simple closed curves with finite total lengths on the plane, for boundary conditions given by integrable real functions.