Conformal Transformations to Other Curves

As we will see in the subsequent sections, it is possible to extend the proof of existence of the Dirichlet problem to boundaries other than the unit circle, through the use of conformal transformations. Therefore, as a preliminary to the proof of further versions of the existence theorem, in this section we will describe such conformal transformations and examine some of their well-known properties, targeting their use here. In order to do this, consider two complex variables $z_{a}$ and $z_{b}$ and the corresponding complex planes, a complex analytic function $\gamma(z)$ defined on the complex plane $z_{a}$ with values on the complex plane $z_{b}$, and its inverse function, which is a complex analytic function $\gamma^{(-1)}(z)$ defined on the complex plane $z_{b}$ with values on the complex plane $z_{a}$,

$$z_{b} = \gamma(z_{a}),$$

$$z_{a} = \gamma^{(-1)}(z_{b}).$$ (10)

Consider a bounded and simply connected open region $S_{a}$ on the complex plane $z_{a}$ and its image $S_{b}$ under $\gamma(z)$, which is a similar region on the complex plane $z_{b}$. It can be shown that if $\gamma(z)$ is analytic on $S_{a}$, is invertible there, and its derivative has no zeros there, then its inverse function $\gamma^{(-1)}(z)$ has these same three properties on $S_{b}$, and the mapping between the two complex planes established by $\gamma(z)$ and $\gamma^{(-1)}(z)$ is conformal, in the sense that it preserves the angles between oriented curves at points where they cross each other. Note that this mapping is a bijection between the two regions, and establishes an equivalence relation that can be extended in a transitive way to other regions.

Consider now that the regions under consideration are the interiors of simple closed curves. One of these curves will be the unit circle $C_{a}$ on the complex plane $z_{a}$, and the other will be a given curve $C_{b}$ on the complex plane $z_{b}$. We will assume that the curve $C_{b}$ has finite total length, for two reasons, one being to ensure that the interior of the curve is a bounded set, and the other being to ensure that the integrals of real functions over the curve $C_{b}$ are integrals over a finite-length, compact domain. Since $\gamma(z_{a})$, being analytic, is in particular a continuous function, the image on the $z_{b}$ plane of the unit circle $C_{a}$ on the $z_{a}$ plane must be a continuous closed curve $C_{b}$. We can also see that $C_{b}$ must be a simple curve, because the fact that $\gamma(z_{a})$ is invertible on $C_{a}$ means that it cannot have the same value at two different points of $C_{a}$, and therefore no two points of $C_{b}$ can be the same. Consequently, the curve $C_{b}$ cannot self-intersect.

We thus see that, so far, we are restricted to simple closed curves $C_{b}$ with finite total lengths. However, there are further limitations on the curves, implied by our hypotheses. Since the transformation is conformal and thus preserves angles, it follows that in this case the smooth unit circle $C_{a}$ is mapped onto another equally differentiable circuit $C_{b}$. One can see this by considering the angles between tangents to the curve $C_{b}$ at pairs of neighboring points, the corresponding elements on the curve $C_{a}$, and the limit of these angles when the two points tend to each other, given that the transformation is conformal. Therefore, with such limitations one cannot map the unit circle onto a square or any other polygon. This limitation can be lifted by allowing the derivative of $\gamma(z_{a})$ to have a finite number of isolated zeros on the curve $C_{a}$, which then implies that the derivative of $\gamma^{(-1)}(z_{b})$ will have a finite number of corresponding isolated singular points on $C_{b}$.

Let us assume that the unit circle $C_{a}$ is described by the real arc-length parameter $\theta$ on the $z_{a}$ plane, and that the curve $C_{b}$ is described by a corresponding real parameter $\lambda$ on the $z_{b}$ plane. Let us assume also that $\lambda$ is chosen in such a way that $\vert d\lambda\vert=\vert dz_{b}\vert$ over the curve $C_{b}$, just as $\vert d\theta\vert=\vert dz_{a}\vert$ over $C_{a}$, which means that $\lambda$ is also an arc-length parameter. Since every point $z_{a}$ on the curve $C_{a}$ is mapped by the conformal transformation onto a corresponding point $z_{b}$ on the curve $C_{b}$, and since a point $z_{a}$ on $C_{a}$ is described by a certain value of $\theta$, while the corresponding point $z_{b}$ on $C_{b}$ is described by a certain value of $\lambda$, it is clear that the complex conformal transformation induces a corresponding real transformation between the values of $\theta$ and the values of $\lambda$,

$$z_{b} = \gamma(z_{a}) \;\;\;\Rightarrow$$

$$\lambda = g(\theta),$$ (11)

where the real function $g(\theta)$ is continuous, differentiable and invertible on $C_{a}$. We will refer to the function $g(\theta)$ as the real transformation induced on the curve $C_{a}$ by the complex conformal transformation $\gamma(z_{a})$. The same is true for the inverse transformation, which induces the inverse function of $g(\theta)$, on the curve $C_{b}$,

$$z_{a} = \gamma^{(-1)}(z_{b}) \;\;\;\Rightarrow$$

$$\theta = g^{(-1)}(\lambda),$$ (12)

where the real function $g^{(-1)}(\lambda)$ is continuous and invertible on $C_{b}$, and also differentiable so long as $C_{b}$ is a differentiable curve. Before we proceed, we must now consider in more detail the question of what is the set of curves $C_{b}$ for which the structure described above can be set up. We assume that this curve is a simple closed curve of finite total length, and the question is whether or not this structure can be set up for an arbitrary such curve. Given the curve $C_{b}$, the only additional objects we need in order to do this is the conformal mapping $\gamma(z_{a})$ and its inverse $\gamma^{(-1)}(z_{b})$, between that curve and the unit circle $C_{a}$.

The existence of these transformation functions can be ensured as a consequence of the famous Riemann mapping theorem, and of the associated results relating to conformal mappings between regions of the complex plane. According to that theorem, a conformal transformation such as the one we described here exists between any bounded simply connected open set of the plane and the open unit disk. In addition to this, one can show that this conformal mapping can be extended to the respective boundaries as a continuous function so long as the boundary curve $C_{b}$ satisfies a certain condition [#!RMPQiu!#].

The condition on $C_{b}$ that implies the existence of the continuous extension to the boundary is that every point on that curve be what is called in the relevant literature a simple point. This means that no point of $C_{b}$ can be a multiple point, which in essence is a point on the boundary that is accessible from the interior via two or more independent continuous paths contained in the interior, that cannot be continuously deformed into each other without crossing the boundary. We can see, therefore, that this condition has a topological character. Note that the presence of a multiple point on the boundary means that, even if the open set under consideration is simply connected, its closure will not be. Therefore, one way to formulate this condition is to simply state that the closure of the bounded simply connected open set must also be simply connected.

Since the existence of a multiple point at the boundary means that this boundary is not a simple curve, it follows that, under the limitations over $C_{b}$ that we have here, the conformal mapping on the open unit disk can always be continuously extended to the unit circle, and hence from the interior of the curve $C_{b}$ to that curve, which is mapped from the unit circle. Therefore, we conclude that it is a known fact that such a conformal transformation exists for all possible simple closed curves $C_{b}$ with finite total lengths, and in particular for all such curves which are also differentiable, in which case the extension is also differentiable on the unit circle $C_{a}$. It is therefore not necessary to impose explicitly any additional hypotheses about the existence of the conformal transformation, regardless of whether or not the curves $C_{b}$ under consideration are differentiable.

Let us close this section with a discussion of the nature of the singularities that appear in the case of simple closed curves $C_{b}$ which are not differentiable at a finite set of points $z_{b,i}$, for $i\in\{1,\ldots,N\}$. The additional difficulty that appears in this case stems from the fact that, if the curve $C_{b}$ is not differentiable at the points $z_{b,i}$, then the derivative of the transformation $\gamma(z_{a})$ has isolated zeros at the corresponding points $z_{a,i}$ on the curve $C_{a}$, and therefore the derivative of the inverse transformation $\gamma^{(-1)}(z_{b})$ has isolated hard singularities at the points $z_{b,i}$. In order to see how this comes about we start by noting that, since we have that

$$\gamma^{(-1)}(\gamma(z_{a})) = z_{a},$$ (13)

for all $z_{a}$ on the closed unit disk, differentiating this equation we get, due to the chain rule,

$$\frac{d\gamma^{(-1)}}{dz_{b}}\, \frac{d\gamma}{dz_{a}}\, = 1.$$ (14)

Therefore, to every point $z_{a,i}$ on $C_{a}$ where the derivative of the transformation has a zero corresponds a point $z_{b,i}$ on $C_{b}$ where the derivative of the inverse transformation diverges to infinity. Taking absolute values we have, in terms of the arc-length parameters $\theta$ and $\lambda$,

$$\left\vert \frac{d\gamma^{(-1)}}{dz_{b}} \right\vert \left\vert \frac{d\gamma}{dz_{a}} \right\vert = \left\vert \frac{dz_{a}}{dz_{b}} \right\vert \left\vert \frac{dz_{b}}{dz_{a}} \right\vert$$

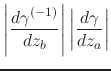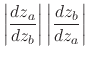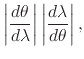$$= \left\vert \frac{d\theta}{d\lambda} \right\vert \left\vert \frac{d\lambda}{d\theta} \right\vert,$$ (15)

which implies that

$$\left\vert \frac{d\theta}{d\lambda} \right\vert \left\vert \frac{d\lambda}{d\theta} \right\vert = 1.$$ (16)

In fact, the real function in the left-hand side of this last equation has a removable singularity at every point where the first derivative in the product diverges and the second one is zero. Consequently, they can be removed by simply redefining the product by continuity at these points. When we approach one of the points $z_{a,i}$, which are characterized by the values $\theta_{i}$ of the parameter $\theta$, along the curve $C_{a}$, we have that

$$\theta \to \theta_{i},$$

$$\lambda \to \lambda_{i}$$

$$\Downarrow$$

$$\left\vert \frac{d\lambda}{d\theta} \right\vert \to 0,$$

$$\left\vert \frac{d\theta}{d\lambda} \right\vert \to \infty,$$ (17)

where the corresponding points $z_{b,i}$ are characterized by the values $\lambda_{i}$ of the parameter $\lambda$, along the curve $C_{b}$. Although the derivative $d\theta/d\lambda$ does, therefore, have hard singularities at $z_{b,i}$, we can show that these are still integrable singularities. We simply integrate the expressions in either side of Equation (16) absolutely over $C_{a}$, thus obtaining

$$\oint_{C_{a}}\vert d\theta\vert\, \left\vert \frac{d\thet... ...t \left\vert \frac{d\lambda}{d\theta} \right\vert = 2\pi.$$ (18)

If we now change variables in this integral from $\theta$ to $\lambda$, we get the integral over $C_{b}$

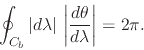$$\oint_{C_{b}}\vert d\lambda\vert\, \left\vert \frac{d\theta}{d\lambda} \right\vert = 2\pi.$$ (19)

This shows that the real function appearing as the integrand in this integral is an integrable real function on $C_{b}$. Therefore the hard singularities where the derivative $d\theta/d\lambda$ diverges to infinity are integrable hard singularities, which therefore have degree of hardness zero. These are also referred to as borderline hard singularities. Note that, as a consequence, the corresponding singularities of the inverse real transformation $g^{(-1)}(\lambda)$ itself must be soft ones, with degrees of softness equal to one.