Integrable Real Functions on the Unit Circle

In a previous paper [#!CAoRFI!#] we have shown that, given an integrable real function on the unit circle, one can define from it a unique inner analytic function whose real part reproduces that real function when restricted to the unit circle. What follows is an outline of the construction of this inner analytic function. Given the integrable real function $f(\theta)$, we define from it, by means of the usual integrals, the Fourier coefficients $\alpha_{0}$, $\alpha_{k}$ and $\beta_{k}$, for $k\in\{1,2,3,\ldots,\infty\}$, and from those coefficients we define the complex Taylor coefficients $c_{0}=\alpha_{0}/2$ and $c_{k}=\alpha_{k}-\mbox{\boldmath$\imath$}\beta_{k}$, for $k\in\{1,2,3,\ldots,\infty\}$. As was shown in [#!CAoRFI!#], the complex power series generated from these coefficients,

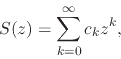$$S(z) = \sum_{k=0}^{\infty} c_{k}z^{k},$$ (4)

always converges to an inner analytic function $w(z)$ within the open unit disk,

$$w(z) = u(\rho,\theta)+\mbox{\boldmath$\imath$}v(\rho,\theta).$$ (5)

As was also shown in [#!CAoRFI!#], the $\rho\to 1_{(-)}$ limit of the real part $u(\rho,\theta)$ reproduces $f(\theta)$ at all points on the unit circle where $w(z)$ does not have hard singularities. It does have hard singularities at all points where $f(\theta)$ does, so we are led to impose that these must be finite in number. However, in some special cases $w(z)$ may have hard singularities at points where $f(\theta)$ does not, and therefore we are led to assume independently that the number of hard singularities of $w(z)$ is finite. For all integrable real functions $f(\theta)$ that correspond to inner analytic functions $w(z)$ which have at most a finite number of hard singularities on the unit circle, we have that

$$f(\theta) = \lim_{\rho\to 1_{(-)}}u(\rho,\theta),$$ (6)

almost everywhere. Since, being the real part of an analytic function, the real function $u(\rho,\theta)$ is a harmonic function defined on the plane, and thus satisfies the Laplace equation within the open unit disk,

$$\nabla^{2}u(\rho,\theta) = 0,$$ (7)

this construction establishes the existence of a solution of the Dirichlet problem on the unit disk or, more precisely, the existence of a solution of the Dirichlet boundary value problem of the Laplace equation on the unit disk. Given the boundary condition $u(1,\theta)=f(\theta)$, the solution is $u(\rho,\theta)$, which by construction satisfies the Laplace equation within the open unit disk and which, also by construction, assumes the values $f(\theta)$ on the unit circle, at least almost everywhere.

Note that, since $f(\theta)$ may have isolated singular points where it diverges to infinity, at which it is, therefore, not well defined, it is clear that $u(\rho,\theta)$ can reproduce $f(\theta)$ only almost everywhere. However, $u(\rho,\theta)$ may fail to reproduce $f(\theta)$ at points other than its hard singularities, namely points where $w(z)$ has hard singularities but $f(\theta)$ happens to have soft ones, due to the way in which the complex singularities of $w(z)$ are oriented with respect to the directions tangent to the unit circle at these singular points. In this case the $\rho\to 1_{(-)}$ limit of $u(\rho,\theta)$ does not exist at such points, and therefore at these points it is not possible to recover the values of $f(\theta)$ in this way.

Note also that, if one introduces some removable singularities of $f(\theta)$ at some points on the unit circle, then this does not change the Fourier coefficients $\alpha_{0}$, $\alpha_{k}$ and $\beta_{k}$, for $k\in\{1,2,3,\ldots,\infty\}$, since these are given by integrals, which implies that it does not change the Taylor coefficients $c_{0}$ and $c_{k}$, for $k\in\{1,2,3,\ldots,\infty\}$, and therefore that it also does not change the corresponding inner analytic function $w(z)$. It follows that $u(\rho,\theta)$ cannot reproduce $f(\theta)$ at these points, if arbitrary real values are attributed to $f(\theta)$ at them. Therefore, we are led to also assume that $f(\theta)$ has no such removable singularities or, equivalently, we are led to assume that all such removable singularities have been removed, and the function redefined by continuity at these trivial singular points.

Here is, then, a complete and precise statement of the Dirichlet problem on the unit disk, followed by the complete set of assumptions to be imposed on $f(\theta)$ in order to ensure the existence of the solution of that problem.

Definition 1   : The Dirichlet Problem on the Unit Disk

Given the unit circle on the complex plane and a real function $f(\theta)$ defined on it, the existence problem of the Dirichlet boundary value problem of the Laplace equation on the unit disk is to show that a function $u(\rho,\theta)$ exists such that it satisfies

$$\nabla^{2}u(\rho,\theta) = 0,$$ (8)

within the open unit disk, and such that it also satisfies

$$u(1,\theta) = f(\theta),$$ (9)

almost everywhere on the unit circle.

In this section, using our results from previous papers, we will establish the following theorem.

Theorem 1   : Given a real function $f(\theta)$ at the boundary of the unit disk, that satisfies the list of conditions described below, there is a solution $u(\rho,\theta)$ of the Dirichlet problem of the Laplace equation within the open unit disk, that assumes the values $f(\theta)$ almost everywhere at its boundary, the unit circle.

Proof 1.1   :

According to the construction introduced in [#!CAoRFI!#] and reviewed above, which provides $u(\rho,\theta)$ starting from $f(\theta)$, the function $u(\rho,\theta)$ that results from that construction is a solution to this problem so long as $f(\theta)$ satisfies the following set of conditions, which ensure that the construction of the inner analytic function $w(z)$ from the real function $f(\theta)$ succeeds, and that the real part $u(\rho,\theta)$ of $w(z)$ reproduces $f(\theta)$ almost everywhere oven the unit circle in the $\rho\to 1_{(-)}$ limit. Apart from the global conditions that the real function $f(\theta)$ be a Lebesgue-measurable function and that it have no removable singularities, the conditions on $f(\theta)$ for this theorem are as follows.

1. The real function $f(\theta)$ is integrable on the unit circle.

2. The number of hard singularities of the corresponding inner analytic function $w(z)$ is finite.

This completes the proof of Theorem 1.

Note that the last condition implies, in particular, that the number of hard singularities of $f(\theta)$, where it is either discontinuous or diverges to infinity, is also finite. Note also that, since the function must be integrable, any hard singularities where it diverges to infinity must be integrable ones, in the real sense of the terms involved. This requires that these hard singularities be all isolated from each other, so that there is a neighborhood around each one of them within which the two lateral asymptotic limits of integrals can be considered. It is important to emphasize that the conditions above over the real functions $f(\theta)$ include functions which are non-differentiable at any number of points, discontinuous at a finite number of points, and unbounded at a finite number of points, thus constituting a rather large set of boundary conditions.