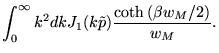 |
|||
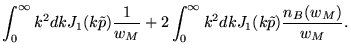 |
|||
| (A.21) |
Nesta seção iremos calcular a forma geral das integrais que aparecem no cálculo das amplitudes no espaço não comutativo. Vamos utilizar para isso algumas das técnicas sugeridas em [50]. Considere assim a seguinte definição:
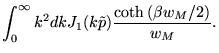 |
|||
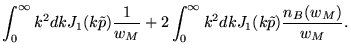 |
|||
| (A.21) |
onde ![]() é definido em (4.41) e
é definido em (4.41) e
![]() (esta integral aparece na Eq. (4.55)).
Além disso, utilizamos a decomposição da cotangente em
termos da funcão distribuição
(esta integral aparece na Eq. (4.55)).
Além disso, utilizamos a decomposição da cotangente em
termos da funcão distribuição
![]() para
obter separadamente as contribuições independente e dependente da
temperatura, respectivamente expressos por
para
obter separadamente as contribuições independente e dependente da
temperatura, respectivamente expressos por ![]() e
e
![]() .
.
Para o termo com ![]() temos
temos
| (A.22) |
Esta integral pode ser facilmente resolvida se utilizarmos alguns
resultados conhecidos a respeito das funções de Bessel ![]() [51], mais especificamente a seguinte relação:
[51], mais especificamente a seguinte relação:
Assim, considerando ![]() ,
, ![]() e
e
![]() podemos reescrever
podemos reescrever ![]() como:
como:
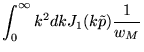 |
|||
![$\displaystyle M^2 \int_1^{\infty} dy \sqrt{y^2 -1} J_1[\tilde{p} M \sqrt{y^2 -1}]$](img872.png) |
|||
![$\displaystyle M^2 e^{- \tilde p M} \left[\frac{1}{\tilde p M} + \frac{1}{(\tilde p
M)^2}\right],$](img873.png) |
(A.24) |
que é exatamente o resultado considerado na Eq. (4.57).
No cálculo do termo dependente da temperatura vamos utilizar a seguinte igualdade para a função distribuição de Bose-Einstein:
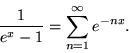 |
(A.25) |
Desta forma podemos reescrever
![]() como
como
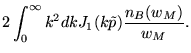 |
|||
![$\displaystyle M^2 \sum_0^{\infty} \int_1^{\infty} dy \sqrt{y^2 - 1} e^{-\beta M
n y } J_1[\tau
\beta M \sqrt{y^2 -1}].$](img877.png) |
(A.26) |
Novamente podemos utilizar a Eq. (A.23), considerando desta vez
![]() ,
,
![]() e
e
![]() . Assim chegamos
ao seguinte resultado:
. Assim chegamos
ao seguinte resultado:
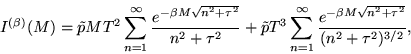 |
(A.27) |
que foi utilizado na Eq. (4.58).