| (A.1) |
O método que iremos utilizar é baseado na referência [39]. Começamos por utilizar a identidade:
de tal forma que substituindo este resultado na Eq. (A.1) obtemos:
![\begin{displaymath}
h_n(y) = \int_0^{\infty} dx \frac{x^n}{\sqrt{x^2 +
y^2}} \le...
...\infty} \frac{\sqrt{x^2+y^2}}{x^2 + y^2 + (2 \pi
m)^2}\right].
\end{displaymath}](img799.png) |
(A.3) |
Cada pedaço da expressão acima contém, em geral, uma
divergência para grandes valores de ![]() . Para garantir que
. Para garantir que ![]() seja finito, é necessário que estas divergências se
compensem no resultado final. Vamos lidar com esta dificuldade definindo uma
quantidade regularizada
seja finito, é necessário que estas divergências se
compensem no resultado final. Vamos lidar com esta dificuldade definindo uma
quantidade regularizada
![]() , como sendo:
, como sendo:
de tal forma que:
| (A.5) |
Usando a igualdade (A.2), podemos
reescrever
![]() como:
como:
![$\displaystyle \int_0^{\infty} dx \frac{x^{n -\epsilon}}{\sqrt{x^2 +
y^2}} \left...
...} + 2
\sum_{m=1}^{\infty} \frac{\sqrt{x^2+y^2}}{x^2 + y^2 + (2 \pi
m)^2}\right]$](img804.png) |
|||
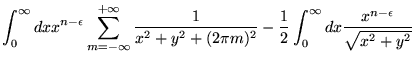 |
|||
| (A.6) |
onde definimos
![]() e
e
![]() respectivamente por:
respectivamente por:
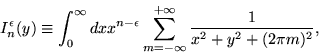 |
(A.7) |
e
Calculando
![]() temos:
temos:
Podemos reescrever a soma que aparece em (A.9) como sendo:
![$\displaystyle \sum_{m= -\infty}^{\infty} \left[y^2 + (2 \pi m)^2\right]^{\frac{n - 1 - \epsilon}{2}}$](img815.png) |
![$\displaystyle y^{n-1-\epsilon} + 2 \sum_{m=1}^{\infty} \left[y^2 + (2
\pi m)^2\right]^{\frac{n-1-\epsilon}{2}}$](img816.png) |
||
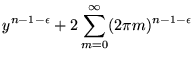 |
|||
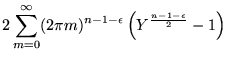 |
|||
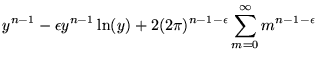 |
|||
 |
|||
| (A.10) |
onde na última passagem realizamos uma expansão em pequenos valores de
![]() . Além disso, definimos a variável
. Além disso, definimos a variável ![]() como:
como:
| (A.11) |
A seguir devemos expandir a expressão acima em torno ![]() (o que
corresponde no nosso caso ao regime de altas temperaturas). Chegamos
assim a:
(o que
corresponde no nosso caso ao regime de altas temperaturas). Chegamos
assim a:
![$\displaystyle \sum_{-\infty}^{\infty} \left[y^2 + (2 \pi m)^2\right]^{\frac{n - 1- \epsilon}{2}}$](img827.png) |
|||
| (A.12) |
onde ![]() são as funções Zeta de Riemann e estamos definindo:
são as funções Zeta de Riemann e estamos definindo:
e
| (A.13) |
Como as funções ![]() tem comportamentos distintos para
argumentos positivos e negativos, vamos considerar um caso particular,
por exemplo
tem comportamentos distintos para
argumentos positivos e negativos, vamos considerar um caso particular,
por exemplo ![]() . Neste caso, a soma torna-se:
. Neste caso, a soma torna-se:
Agora usando que:
| (A.15) |
e as seguintes relações para as funções Zeta de Riemann:
e
| (A.16) |
podemos reescrever
![]() com o uso das
Eqs. (A.9) e (A.14) como:
com o uso das
Eqs. (A.9) e (A.14) como:
Calculando
![]() a partir da Eq. (A.8), temos:
a partir da Eq. (A.8), temos:
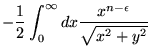 |
|||
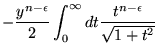 |
|||
![$\displaystyle - \frac{y^{n - \epsilon}}{4} \frac{\Gamma \left( \frac{n +1 -
\ep...
...- \epsilon}{2}\right)\sin \left[\pi \left(\frac{\epsilon
-n}{2}\right)\right]}.$](img850.png) |
(A.18) |
Em particular, para ![]() , obtemos:
, obtemos:
Finalmente, unindo (A.17) e (A.19) chegamos a:
| (A.20) |
que foi o resultado utilizado na Eq. (3.54).