The Critical Line

We will now calculate the Gaussian-Perturbative approximation for the particular observable ${\mathbf O}[\vec{\varphi}']=\varphi_{\mathfrak{N}}(n_{\mu}')$, at some arbitrary point $n_{\mu}'$. If we write the observable in terms of the shifted field we get

$$\begin{eqnarray*} {\mathbf O}[\vec{\varphi}'] & = & \varphi_{\mathfrak{N}}(n_{\mu}') \\ & = & \varphi_{\mathfrak{N}}'(n_{\mu}')+v_{0}. \end{eqnarray*}$$

In order to get the equation of the critical line we impose, in a self-consistent way, that we in fact have

$$\left\langle\varphi_{\mathfrak{N}}(n_{\mu}')\right\rangle = v_{0},$$

which is the same as stating that

$$\left\langle\varphi_{\mathfrak{N}}'(n_{\mu}')\right\rangle = 0.$$

In the first-order Gaussian-Perturbative approximation this becomes

$$\begin{eqnarray*} \left\langle\varphi_{\mathfrak{N}}'(n_{\mu}')\right\rangle &... ...{V}[\vec{\varphi}'] \right\rangle_{0} \right\} \\ & = & 0. \end{eqnarray*}$$

Since we have $\left\langle\varphi_{\mathfrak{N}}'(n_{\mu}')\right\rangle_{0}=0$, because this observable is field-odd and the Gaussian action $S_{0}[\vec{\varphi}']$ is field-even, we get for the critical line the simple equation, known as the tadpole equation,

$$\left\langle \varphi_{\mathfrak{N}}'(n_{\mu}')S_{V}[\vec{\varphi}'] \right\rangle_{0} = 0.$$

The expectation value shown here is calculated in Appendix A, given in Equation (A.4), and the result is

$$\left\langle \varphi_{\mathfrak{N}}'(n_{\mu}')S_{V}[\vec{\... ...thfrak{N}}^{2} \right] - j_{0} } {\alpha_{\mathfrak{N}}}.$$

The parameter $\alpha_{\mathfrak{N}}$ cancels off from our equation, and thus we are left with the result

$$j_{0} = v_{0} \left\{ \lambda v_{0}^{2} + \alpha + ... ...a_{0}^{2} + 3 \sigma_{\mathfrak{N}}^{2} \right] \right\},$$ (C.4)

in which we now isolated on the left-hand side the term with the external source. This gives the general relation between $j_{0}$ and $v_{0}$ at each point $(\alpha,\lambda)$ of the parameter space of the model. As we shall see later, from this result we can determine the critical behavior of the model and derive the equation of the critical line.

The quantity $\sigma_{0}$ is the width or variance of the local distribution of values of the field components $\varphi_{i}'(n_{\mu})$, with $i=1,\ldots,\mathfrak{N}-1$, in the measure of $S_{0}[\vec{\varphi}']$,

$$\begin{eqnarray*} \sigma_{0}^{2} & = & \left\langle \varphi_{i}'^{2}(n_{\mu}... ... \sum_{k_{\mu}}^{N^{d}} \frac{1}{\rho^{2}(k_{\mu})+\alpha_{0}}, \end{eqnarray*}$$

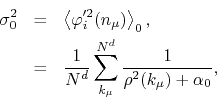
as one can see in Appendix B, Equation (B.6), and has the following interesting properties, so long as $d\geq 3$. First, it is independent of the position $n_{\mu}$, as translation invariance would require. Second, for $d\geq 3$ it has a finite and non-zero $N\to\infty$ limit, so long as $\alpha_{0}=a^{2}m_{0}^{2}$ with a finite value of $m_{0}$ in the limit. Finally, the value of $\sigma_{0}$ in the limit does not depend on the value of $m_{0}$ in that same limit. Analogously, the quantity $\sigma_{\mathfrak{N}}$ is associated to the remaining field component $\varphi_{\mathfrak{N}}'(n_{\mu})$ and to the mass parameter $\alpha_{\mathfrak{N}}$, and has these same properties. In fact, $\sigma_{0}$ and $\sigma_{\mathfrak{N}}$ have exactly the same value in the $N\to\infty$ limit.