Up: Gaussian-Perturbative Calculations with a Previous: The Expectation Value of
We give here a series of formulas and derivations involving Gaussian integrals, Gaussian expectation values and lattice sums, in the context the model discussed in this paper, which are used for the calculations presented. All these can be derived from the basic result in momentum space
where ![]() is either
is either ![]() or
or
![]() , depending on
the field component involved, and where
, depending on
the field component involved, and where
![]() are the
eigenvalues of the discrete Laplacian on the lattice, which are given by
are the
eigenvalues of the discrete Laplacian on the lattice, which are given by
Since in the measure of
![]() the modes are decoupled in
momentum space, the same expectation value with two different momenta
the modes are decoupled in
momentum space, the same expectation value with two different momenta
![]() and
and ![]() is zero by simple parity arguments. We use the
notation for the two-point functions in position space,
is zero by simple parity arguments. We use the
notation for the two-point functions in position space,
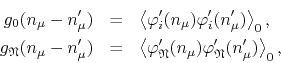
for
![]() . These are, of course, the inverse Fourier
transforms of the corresponding two-point functions in momentum space,
. These are, of course, the inverse Fourier
transforms of the corresponding two-point functions in momentum space,
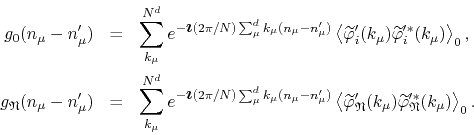
In order to write this explicitly we may use the Fourier transforms of the
fields, for example in the case of the
![]() field
component,
field
component,
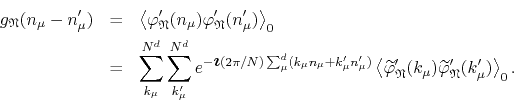
The expectation value in momentum space in non-zero only if we have
![]() , in which case we have the result, which can be
obtained from Equation (B.1) above,
, in which case we have the result, which can be
obtained from Equation (B.1) above,
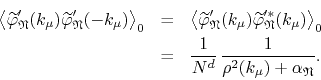
This eliminates one of the momentum-space sums, and thus we get
which is just the statement that
![]() is the
inverse Fourier transform of the momentum-space propagator. Note that this
is necessarily real, and that therefore the imaginary part of the
right-hand side vanishes. In a completely similar way, we have the
corresponding result for the other field
is the
inverse Fourier transform of the momentum-space propagator. Note that this
is necessarily real, and that therefore the imaginary part of the
right-hand side vanishes. In a completely similar way, we have the
corresponding result for the other field
![]() components, with
components, with
![]() ,
,
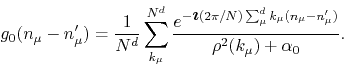
The following sum involving
![]() can also be easily
calculated, using once more the Fourier transforms,
can also be easily
calculated, using once more the Fourier transforms,
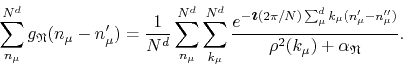
The orthogonality relation can be used to simplify this expression, and thus we get
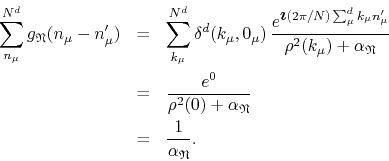
This is simply the zero-mode of the propagator. The same can be done for the other components of the field, so we conclude that
A similar sum with two chained factors of
![]() can
be calculated in a similar way. Using the Fourier expressions of
can
be calculated in a similar way. Using the Fourier expressions of
![]() and
and
![]() we get
we get
![\begin{eqnarray*}
\lefteqn
{
\sum_{n_{\mu}}^{N^{d}}
g_{0}(n_{\mu}-n_{\mu}')\...
...mu}''n_{\mu}'')}
}
{
[\rho^{2}(k_{\mu}'')+\alpha_{0}]^{2}
}.
\end{eqnarray*}](img367.png)
We see therefore that we get the sum expressed as a Fourier transform, with the general structure of a two-point function,
A similar result is true, of course, for the remaining field component
The squared dispersions, also referred to as widths or variances of the fields at a given site, are denoted as
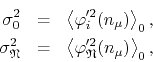
for
![]() . Using the expression of the two-point function in
terms of Fourier components we may write these explicitly as
. Using the expression of the two-point function in
terms of Fourier components we may write these explicitly as
In terms of these quantities the following decompositions of higher-point
functions can be established, always for
![]() ,
,
It is also not difficult to expand and calculate the following sums,
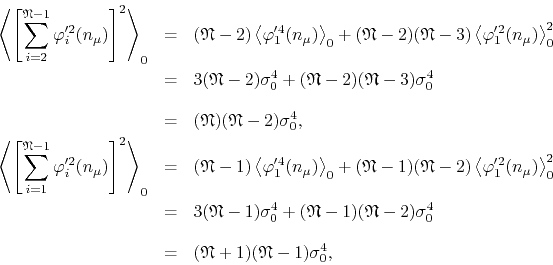
so that we get the results