The Expectation Value of $\varphi_{\mathfrak{N}}'(n_{\mu}')S_{V}[\vec{\varphi}']$

Let us now calculate the expectation value

$$\left\langle \varphi_{\mathfrak{N}}'(n_{\mu}')S_{V}[\vec{\varphi}'] \right\rangle_{0}.$$

Since $S_{0}[\vec{\varphi}']$ is field-even, all expectation values of field-odd observables are zero when calculated in its measure. Therefore it is necessary that the observables be field-even if their expectation values are to be non-zero. Since in this case we have an explicit factor of $\varphi_{\mathfrak{N}}'(n_{\mu}')$, it follows that only the field-odd part of $S_{V}[\vec{\varphi}']$ will contribute to this expectation value,

$$\left\langle \varphi_{\mathfrak{N}}'(n_{\mu}')S_{V}[\vec{\... ...'(n_{\mu}')S_{V,{\rm odd}}[\vec{\varphi}'] \right\rangle_{0}.$$

If we write the expectation value out, using the form of the action $S_{V,{\rm odd}}[\vec{\varphi}']$ given in Equation (A.1), we get

$$\begin{eqnarray*} \left\langle \varphi_{\mathfrak{N}}'(n_{\mu}')S_{V}[\vec{\va... ...)\varphi_{\mathfrak{N}}'(n_{\mu}') \right\rangle_{0} \right\}. \end{eqnarray*}$$

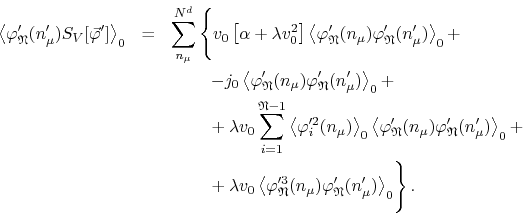
The expectation values in the first three terms turn out to be just the position-space propagator for the $\varphi_{\mathfrak{N}}'(n_{\mu})$ field component. From Appendix B, Equation (B.2), we get

$$g_{\mathfrak{N}}(n_{\mu}-n_{\mu}') = \frac{1}{N^{d}} \su... ..._{\mu}-n_{\mu}')}} {\rho^{2}(k_{\mu})+\alpha_{\mathfrak{N}}},$$

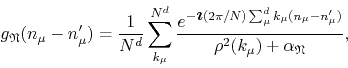
which is just the statement that $g_{\mathfrak{N}}(n_{\mu}-n_{\mu}')$ is the inverse Fourier transform of the momentum-space propagator. We also have the corresponding result for the other field $\mathfrak{N}-1$ components, with $i\neq\mathfrak{N}$,

$$\begin{eqnarray*} g_{0}(n_{\mu}-n_{\mu}') & = & \left\langle \varphi_{i}'(n_... ...^{d}k_{\mu}(n_{\mu}-n_{\mu}')}} {\rho^{2}(k_{\mu})+\alpha_{0}}. \end{eqnarray*}$$

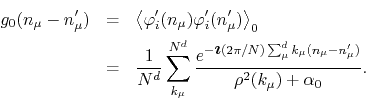
The second expectation value that we must calculate, with $i\neq\mathfrak{N}$, is simply

$$\begin{eqnarray*} g_{0}(0) & = & \left\langle \varphi_{i}'^{2}(n_{\mu}) \ri... ... \sum_{k_{\mu}}^{N^{d}} \frac{1}{\rho^{2}(k_{\mu})+\alpha_{0}}. \end{eqnarray*}$$

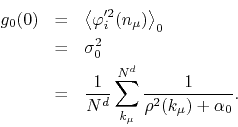
The third expectation value that we must calculate can be found in Appendix B, Equation (B.9), and can be shown to be given in terms of the first one by

$$\left\langle \varphi_{\mathfrak{N}}'^{3}(n_{\mu})\varphi_{... ...\sigma_{\mathfrak{N}}^{2}\,g_{\mathfrak{N}}(n_{\mu}-n_{\mu}').$$

We are thus left with a simpler form for the expectation value,

$$\begin{eqnarray*} \left\langle \varphi_{\mathfrak{N}}'(n_{\mu}')S_{V}[\vec{\va... ...m}{4ex} - j_{0} g_{\mathfrak{N}}(n_{\mu}-n_{\mu}') \right\}. \end{eqnarray*}$$

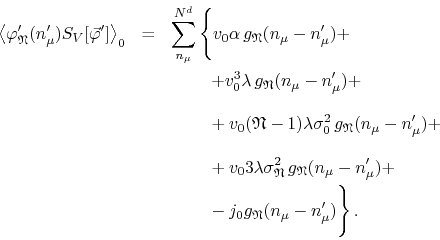
In all terms the only quantity still depending on $n_{\mu}$ is $g_{\mathfrak{N}}(n_{\mu}-n_{\mu}')$, so that we can write this equation as

$$\left\langle \varphi_{\mathfrak{N}}'(n_{\mu}')S_{V}[\vec{\... ...} \sum_{n_{\mu}}^{N^{d}} g_{\mathfrak{N}}(n_{\mu}-n_{\mu}').$$

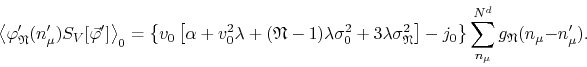
Using Equation (B.3), which gives this final sum, we may finally write

$$\left\langle \varphi_{\mathfrak{N}}'(n_{\mu}')S_{V}[\vec{\... ...thfrak{N}}^{2} \right] - j_{0} } {\alpha_{\mathfrak{N}}}.$$ (A.4)