The Expectation Value of $S_{V}[\vec{\varphi}']$

We now calculate the expectation value

$$\left\langle S_{V}[\vec{\varphi}'] \right\rangle_{0}.$$

Only the field-even part of the action will yield a non-zero result, so that we have

$$\left\langle S_{V}[\vec{\varphi}'] \right\rangle_{0} = ... ...t\langle S_{V,{\rm even}}[\vec{\varphi}'] \right\rangle_{0}.$$

Using the form of $S_{V,{\rm even}}[\vec{\varphi}']$ shown in Equation (A.2) we get for this expectation value

$$\begin{eqnarray*} \lefteqn { \left\langle S_{V}[\vec{\varphi}'] \right\rang... ...arphi_{\mathfrak{N}}'^{4}(n_{\mu}) \right\rangle_{0} \right\}. \end{eqnarray*}$$

Most of the remaining expectation values can be written in terms of $\sigma_{0}$ and $\sigma_{\mathfrak{N}}$, if we recall that it can be shown that for $i\neq\mathfrak{N}$ we have

$$\left\langle \varphi_{i}'^{4}(n_{\mu}) \right\rangle_{0} = 3\sigma_{0}^{2},$$

while for $i=\mathfrak{N}$ we have, in a similar way,

$$\left\langle \varphi_{\mathfrak{N}}'^{4}(n_{\mu}) \right\rangle_{0} = 3\sigma_{\mathfrak{N}}^{2},$$

as one can find in Appendix B, Equation (B.8). Given all this, we may write for our expectation value

$$\begin{eqnarray*} \left\langle S_{V}[\vec{\varphi}'] \right\rangle_{0} & = &... ...} + \frac{3\lambda}{4}\, \sigma_{\mathfrak{N}}^{4} \right\}. \end{eqnarray*}$$

The remaining expectation value of the sum shown can be found in Appendix B, Equation (B.15),

$$\left\langle \left[ \sum_{i=1}^{\mathfrak{N}-1} \varphi_... ...e{0em}{4ex} (\mathfrak{N}+1)(\mathfrak{N}-1) \sigma_{0}^{4}.$$

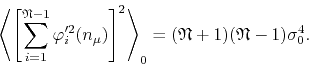
Using this result we get for our expectation value

$$\begin{eqnarray*} \left\langle S_{V}[\vec{\varphi}'] \right\rangle_{0} & = &... ...2} + \frac{3\lambda}{4}\, \sigma_{\mathfrak{N}}^{4} \right]. \end{eqnarray*}$$

Note that all the sums can now be done, so that we can write our result in the simpler form

$$\left\langle S_{V}[\vec{\varphi}'] \right\rangle_{0} = N^{d} \left[ \frac{\alpha-\alpha_{0}+\lambda v_{0}^{2}}{2}\, (\ma... ...pha_{\mathfrak{N}}+3\lambda v_{0}^{2}}{2}\, \sigma_{\mathfrak{N}}^{2} + \right.$$

$$\hspace{2.2em} \left. + \frac{\lambda}{4}\, (\mathfrak{N}^{2}-1) ... ...ma_{\mathfrak{N}}^{2} + \frac{3\lambda}{4}\, \sigma_{\mathfrak{N}}^{4} \right].$$ (A.5)