Next: The Expectation Value of Up: Calculation of Expectation Values Previous: The Expectation Value of
We now calculate the expectation value
Once more only the field-even part of the action will yield a non-zero result, so that we have
Using the form of
![]() shown in
Equation (A.3), and if we already replace the expectation values
of squared fields by
shown in
Equation (A.3), and if we already replace the expectation values
of squared fields by ![]() or
or
![]() whenever possible, as
well as replace
whenever possible, as
well as replace
![]() by
by
![]() , we get
, we get
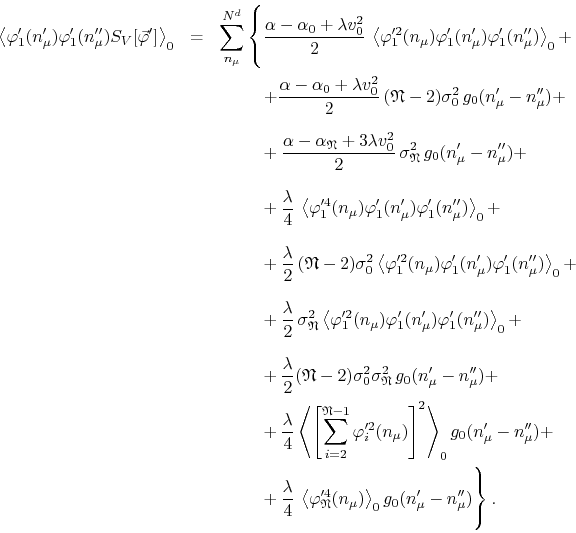
We may now use the known value of the expectation value of the squared sum. From Appendix B, Equation (B.14), we get
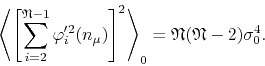
We may also use the fact that it can be shown that
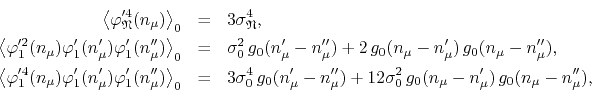
also found in Appendix B, Equations (B.8), (B.10) and (B.12), in order to write for our expectation value
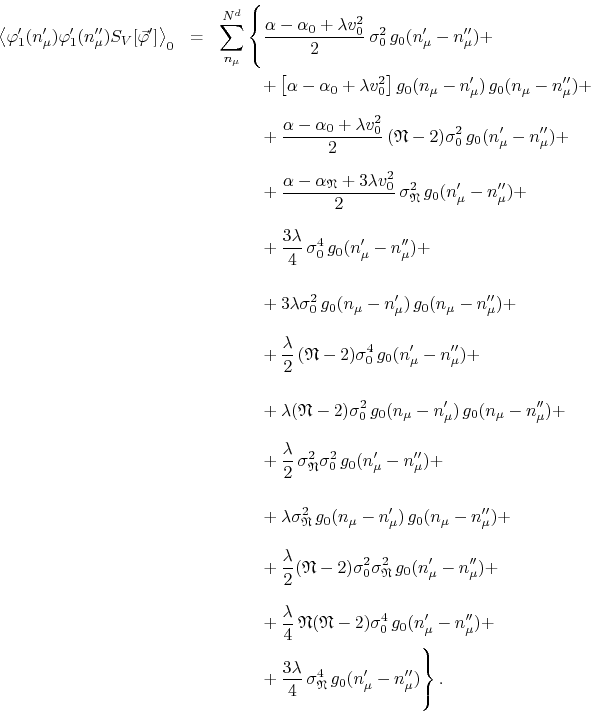
Next we group all terms containing
![]() and
simplify to get
and
simplify to get
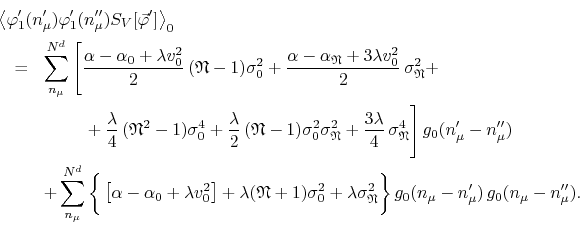
The sum over ![]() can now be done in all terms in the first group,
yielding
can now be done in all terms in the first group,
yielding
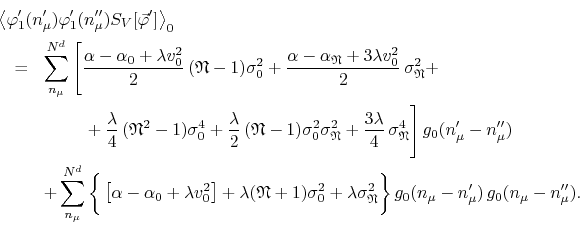
We must now perform the sum indicated. This is easily done using Fourier transforms. From Appendix B, Equation (B.4), we get
![\begin{displaymath}
\sum_{n_{\mu}}^{N^{d}}
g_{0}(n_{\mu}-n_{\mu}')\,
g_{0}(n_...
...mu}'-n_{\mu}'')}
}
{
[\rho^{2}(k_{\mu})+\alpha_{0}]^{2}
},
\end{displaymath}](img337.png)
which is expressed as a Fourier transform, with the general structure of a two-point function. We have therefore the final result,