Next: General Singularity Factorization Up: Fourier Theory on the Previous: Monotonicity Extensions
One of the interesting facts that follow from the analysis in the previous
paper [1] is that, since the limiting function of a DP Fourier
series is always given by the limit of the corresponding inner analytic
function from within the open unit disk to the unit circle, in any open
subset of that circle where ![]() is analytic it is also
is analytic it is also ![]() along
along ![]() . Therefore a DP Fourier series that converges in a
piecewise fashion between two consecutive singularities of
. Therefore a DP Fourier series that converges in a
piecewise fashion between two consecutive singularities of ![]() does so
to a piecewise section of a
does so
to a piecewise section of a ![]() function. This means that it
should be possible to recover the
function. This means that it
should be possible to recover the ![]() function involved in each
section, and also that it should be possible to represent them by series
that converge at a faster rate and can thus be differentiated at least a
few times. In this section we will show how one can accomplish the latter
goal.
function involved in each
section, and also that it should be possible to represent them by series
that converge at a faster rate and can thus be differentiated at least a
few times. In this section we will show how one can accomplish the latter
goal.
We start with a simple case, which in fact we have already demonstrated
completely in the previous section. The proof of convergence of DP Fourier
series with monotonic coefficients described in
Subsection 5.1 can be understood as a process of
factorization of the singularity of the inner analytic function ![]() .
Interpreted in terms of
.
Interpreted in terms of ![]() we may write the relation between that
series and the corresponding center series
we may write the relation between that
series and the corresponding center series ![]() as
as
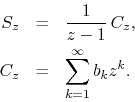
As we have shown before, since ![]() converges to an inner analytic
function
converges to an inner analytic
function ![]() , so does
, so does ![]() , and hence we have
, and hence we have
where ![]() converges to
converges to ![]() . What was done here is to factor
out of
. What was done here is to factor
out of ![]() a simple pole at the point
a simple pole at the point ![]() . Hence the original series
. Hence the original series
![]() , which is not absolutely or uniformly convergent and is associated
to an inner analytic function that has a borderline hard singularity at
, which is not absolutely or uniformly convergent and is associated
to an inner analytic function that has a borderline hard singularity at
![]() , is translated into a series
, is translated into a series ![]() which is absolutely and
uniformly convergent, and that is associated to an inner analytic function
that has a borderline soft singularity at that point. Note that the
which is absolutely and
uniformly convergent, and that is associated to an inner analytic function
that has a borderline soft singularity at that point. Note that the
![]() transformation does not change the maximum disk of
convergence or the location of any singularities. Just like logarithmic
integration, it just softens the existing singularities.
transformation does not change the maximum disk of
convergence or the location of any singularities. Just like logarithmic
integration, it just softens the existing singularities.