General Singularity Factorization

If we think about our general scheme of classification of singularities and modes of convergence, we can see that so long as that scheme holds this process of factoring out singularities should always work, regardless of any hypothesis about the coefficients, such as that they be monotonic. So long as the coefficients of the original DP trigonometric series lead to the construction of an inner analytic function, and so long as that inner analytic function has at most a finite set of dominant singularities over the unit circle, which are not infinitely hard ones such as essential singularities, it should be possible to do this, and hence produce another related series in which the dominant singularities are softened.

Here is how this procedure works. Given a certain DP Fourier series with coefficients $a_{k}$, we construct the series $S_{z}$ and thus the inner analytic function $w(z)$ and determine the set of dominant singularities that it has on the unit circle, which we assume are $N$ in number. Independently of the degree of hardness or softness of these singularities, we now introduce simple poles at each dominant singularity,

$$\begin{eqnarray*} S_{z} & = & \frac {(z-z_{1})\ldots(z-z_{N})} {(z-z_{1})\l... ... S_{z} \\ & = & \frac{1}{(z-z_{1})\ldots(z-z_{N})}\, C_{z}, \end{eqnarray*}$$

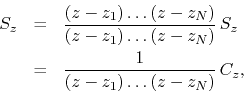
where the new series is defined by

$$C_{z} = P_{N}(z) S_{z},$$

where $P_{N}(z)$ is a polynomial of the order indicated,

$$P_{N}(z) = (z-z_{1})\ldots(z-z_{N}).$$

This polynomial and the original series $S_{z}$ can then be manipulated algebraically in order to produce an explicit expression for the new series $C_{z}$, which we will still call the center series of $S_{z}$. Let us show that $C_{z}$ converges to an inner analytic function $\gamma(z)$. Since $S_{z}$ converges to an analytic function $w(z)$ on the open unit disk, it is at once apparent that $C_{z}$ also converges to an analytic function on that disk, since $P_{N}(z)$ is a polynomial and hence an analytic function over the whole complex plane. Also, since $S_{z}=0$ at the point $z=0$, it follows at once that $C_{z}=0$ on that same point.

Let us now recall that $S_{z}$ is a power series generated by a FC pair of DP Fourier series, and therefore that its real and imaginary parts have definite parities. Therefore, the inner analytic function $w(z)$ that it converges to also has real and imaginary parts with definite parities. As we showed before, its real part is even on $\theta$, and its imaginary part is odd on $\theta$. Therefore, the singularities of the function $w(z)$ must come in pairs, unless they are located at $\theta=0$ or $\theta=\pm\pi$. This means that, if there is a singularity at a point $z_{1}$ on the unit circle away from the real axis, then there is an essentially identical one at $z_{1}^{*}$,

$$\begin{eqnarray*} z_{1} & = & \cos(\theta_{1}) + \mbox{\boldmath$\imath$} ... ...os(-\theta_{1}) + \mbox{\boldmath$\imath$} \sin(-\theta_{1}), \end{eqnarray*}$$

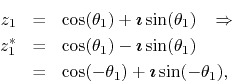
possibly with the overall sign reversed. It follows that, if we want to factor out the singularities on both points, we must choose the factors that constitute $P_{N}(z)$ in pairs of factors at complex-conjugate points, except possibly for a couple of points over the real axis. Assuming for example that $z_{2}$ is real, we have to use something like

$$P_{N}(z) = (z-z_{1}) (z-z_{1}^{*}) \times (z-z_{2}) \times (z-z_{3}) (z-z_{3}^{*}) \times \ldots\;.$$

If we restrict the polynomial to the real axis we get

$$P_{N}(x) = (x-z_{1}) (x-z_{1}^{*}) \times (x-z_{2}) \times (x-z_{3}) (x-z_{3}^{*}) \times \ldots\;.$$

If we now take the complex conjugate of $P_{N}(x)$ we see that in fact nothing changes,

$$P_{N}^{*}(x) = (x-z_{1}^{*}) (x-z_{1}) \times (x-z_{2}) \times (x-z_{3}^{*}) (x-z_{3}) \times \ldots\;.$$

Since we thus conclude that $P_{N}^{*}(x)=P_{N}(x)$, it follows that $P_{N}(x)$ is a real polynomial over the real axis. Since the series $S_{z}$ converges to an inner analytic function $w(z)$, which also reduces to a real function on the interval $(-1,1)$ of the real axis, it follows that $\gamma(z)$ reduces to a real function on the interval $(-1,1)$ of the real axis as well. This establishes that the function $\gamma(z)$ has all the required properties and is therefore an inner analytic function.

Assuming that the series $S_{z}$ is convergent, and thus that $w(z)$ has at most borderline hard singularities, this new series $C_{z}$ generates a new inner analytic function $\gamma(z)$ that has only soft singularities and hence $C_{z}$ converges absolutely and uniformly to a continuous function. From that function and the explicit poles we can then reconstruct the original function, in a piecewise fashion between pairs of adjacent dominant singularities. If the series $S_{z}$ was already absolutely and uniformly convergent, the new center series $C_{z}$ will allow one to take one more derivative, compared with the situation regarding $S_{z}$.

Note that between two adjacent singularities the function $w(z)$ is analytic over sections of the unit circle, and hence piecewise $C^{\infty}$, so that this process can be taken, in principle, as far as one wishes, by the iteration of this procedure. In order to do this one has to re-examine the set of singularities of the resulting function $\gamma(z)$ because, with the softening of the dominant singularities, there may be now more singularities just as soft as those in the first set became. This will generate a new set of dominant singularities, and assuming that this set is also finite in number, one may iterate the procedure. The result will be a series that not only is absolutely and uniformly convergent, but is also one that can be differentiated one more time and still result in an equally convergent series.

Note also that we may as well start the process with a series that if flatly divergent, and that there is nothing to prevent us from recovering from it the original function, from which the coefficients were obtained. This can always be done, at least in principle, if the inner analytic function has at most a finite number of isolated singularities on the unit circle, each one with a finite degree of hardness. On the other hand, it cannot be done if there is an infinite number of dominant singularities, or if any individual singularity is an infinitely hard one, such as an essential singularity.

Arguably the most difficult step in this process is the determination of the singularities of the inner analytic function from the series. If there is enough information about the real function that originated it, or about the circumstances of the application involved, it may be possible to guess at the set of singularities. Otherwise, this information has to be obtained from the structure of the series itself.

However, this may not be such a grave difficulty as it might appear at first, since a given singularity structure characterizes a whole class of series, not a single series. For example, all series which have monotonic coefficients with step $1$ have a single dominant singularity at $z=1$. Series which have monotonic coefficients with step $1$ and a factor of $(-1)^{k}$ added to the coefficients have a single dominant singularity at $z=-1$. Series with monotonic coefficients with step $2$ have two dominant singularities, at $z=1$ and at $z=-1$. Series with monotonic coefficients with step $2$ and a factor of $(-1)^{j}$ added to the coefficients have two dominant singularities, at $z=\mbox{\boldmath$\imath$}$ and at $z=-\mbox{\boldmath$\imath$}$, and so on. In Appendix B we will give several simple examples of the construction of center series.

Observe also that this whole procedure is safe in the sense that if one guesses erroneously at the singularities, the worst that can happen is that no improvement in convergence is obtained. Besides, at least in principle the factorization process can be considered in reverse, in the sense that one may analyze the structure of the series $S_{z}$ in order to discover what set of factors would do the trick of resulting in a series $C_{z}$ with coefficients that go to zero faster than the original ones. If this problem is solvable, it in fact determines the location of the dominant singularities of the inner analytic function over the unit circle, by what turns out to have the nature of a purely algebraic method, leading to a polynomial $P_{N}(z)$ that implements the softening of the dominant singularities.