Next: Monotonicity Extensions Up: Monotonic Series Previous: Monotonic Series
Within the set of all series ![]() which are very weakly convergent,
there is a subset of series that all converge almost everywhere, as we
will now show. This is the class of series
which are very weakly convergent,
there is a subset of series that all converge almost everywhere, as we
will now show. This is the class of series ![]() that have coefficients
that have coefficients
![]() that converge monotonically to zero. This monotonicity of the
coefficients can, therefore, be used as a convergence test. No statement
at all has to be made about the speed of convergence to zero, but we may
as well focus our attention on series of type
that converge monotonically to zero. This monotonicity of the
coefficients can, therefore, be used as a convergence test. No statement
at all has to be made about the speed of convergence to zero, but we may
as well focus our attention on series of type ![]() , with
coefficients behaving as
, with
coefficients behaving as
![]() with
with ![]() , which
are those for which this analysis is most useful, since in this case the
sum
, which
are those for which this analysis is most useful, since in this case the
sum
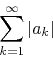
diverges to infinity and the series is therefore not absolutely or
uniformly convergent. For simplicity we will take the case in which
![]() for all
for all ![]() , but the argument can be easily generalized to
several other cases, as will be discussed later on. Let us consider then
the series
, but the argument can be easily generalized to
several other cases, as will be discussed later on. Let us consider then
the series
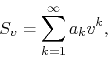
where ![]() for all
for all ![]() ,
,
![]() for all
for all ![]() and
and
Such a series can be shown to converge for ![]() by the use of
the Dirichlet test. For
by the use of
the Dirichlet test. For ![]() it diverges to positive infinity along
the real axis, and therefore satisfies the hypotheses defining a series of
type
it diverges to positive infinity along
the real axis, and therefore satisfies the hypotheses defining a series of
type ![]() in a regular integral-differential chain. It is not too
difficult to show that, for any non-zero value of
in a regular integral-differential chain. It is not too
difficult to show that, for any non-zero value of ![]() in the periodic
interval, the Dirichlet partial sums
in the periodic
interval, the Dirichlet partial sums
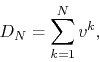
are contained within a closed disk of radius
centered at the point
of the complex plane, for all values of ![]() . The absolute values
. The absolute values ![]() of the Dirichlet partial sums are therefore bounded by a constant for all
of the Dirichlet partial sums are therefore bounded by a constant for all
![]() , and since the coefficients go monotonically to zero, the Dirichlet
test applies and the series
, and since the coefficients go monotonically to zero, the Dirichlet
test applies and the series ![]() is convergent.
is convergent.
We will, however, demonstrate the convergence in another way, which we
believe to be more fruitful, and more directly related to our problem
here. What we will do is to construct another expression, involving
another DP Fourier series, that converges to the same function and, unlike
![]() , does so absolutely and uniformly almost everywhere. Consider then
the following algebraic passage-work for our series, for
, does so absolutely and uniformly almost everywhere. Consider then
the following algebraic passage-work for our series, for ![]() ,
which is equivalent to
,
which is equivalent to ![]() . We start by multiplying and dividing the
series by the factor
. We start by multiplying and dividing the
series by the factor ![]() , and distributing the one in the numerator,
, and distributing the one in the numerator,
![\begin{eqnarray*}
S_{v}
& = &
\frac{v-1}{v-1}
\sum_{k=1}^{\infty}
a_{k}v^{k...
...fty}
a_{k}v^{k+1}
-
\sum_{k=1}^{\infty}
a_{k}v^{k}
\right].
\end{eqnarray*}](img112.png)
We now change the index of the first series, in order to be able to join the two resulting series,
![\begin{eqnarray*}
S_{v}
& = &
\frac{1}{v-1}
\left[
\,
\sum_{k=2}^{\infty}
...
...
a_{1}v
+
\sum_{k=2}^{\infty}
(a_{k-1}-a_{k})v^{k}
\right].
\end{eqnarray*}](img113.png)
If we now define the new coefficients ![]() and
and
![]() for
for ![]() , we have a new series
, we have a new series ![]() , which we
name the center series of
, which we
name the center series of ![]() , so that we have
, so that we have
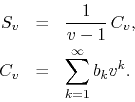
The name we chose for this series comes from the fact that it describes
the relatively small drift in the complex plane of the instantaneous
center of rotation of the convergence process of the ![]() series.
Specially for
series.
Specially for
![]() with the values of
with the values of ![]() closer to
zero, the convergence process of the
closer to
zero, the convergence process of the ![]() series proceeds in a long,
slow spiral around the limiting point, while that of the
series proceeds in a long,
slow spiral around the limiting point, while that of the ![]() series
goes more or less directly to it. Let us now show that
series
goes more or less directly to it. Let us now show that ![]() is
absolutely and thus uniformly convergent. We simply consider the series
is
absolutely and thus uniformly convergent. We simply consider the series
![]() of the absolute values of the terms of
of the absolute values of the terms of ![]() . Since
. Since
![]() , we get
, we get
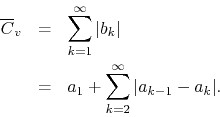
Since the coefficients ![]() decrease monotonically to zero, we have
decrease monotonically to zero, we have
![]() and thus we may write
and thus we may write
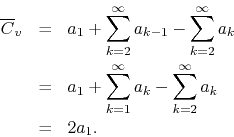
Since ![]() is some finite real number, this establishes an upper bound
for
is some finite real number, this establishes an upper bound
for
![]() . Since this series is a sum of positive terms and
thus monotonically increasing, this implies that it converges and
therefore that
. Since this series is a sum of positive terms and
thus monotonically increasing, this implies that it converges and
therefore that ![]() is absolutely convergent. Since the bound and
therefore the criterion of convergence are independent of
is absolutely convergent. Since the bound and
therefore the criterion of convergence are independent of ![]() , the
convergence is also uniform. Therefore, for
, the
convergence is also uniform. Therefore, for ![]() we may evaluate
we may evaluate
![]() by first evaluating
by first evaluating ![]() and then multiplying the result by the
simple pole
and then multiplying the result by the
simple pole ![]() .
.
This proves not only the absolute and uniform convergence of the series
![]() everywhere on the unit circle, it also implies the convergence of
the original series
everywhere on the unit circle, it also implies the convergence of
the original series ![]() at all points except the special point
at all points except the special point ![]() ,
which corresponds to
,
which corresponds to ![]() . Obviously the
. Obviously the ![]() series does not
converge absolutely or uniformly, but it does converge at all points
except
series does not
converge absolutely or uniformly, but it does converge at all points
except ![]() . We see therefore that the monotonicity of the coefficients
can be used as a test for simple point-wise convergence of the
. We see therefore that the monotonicity of the coefficients
can be used as a test for simple point-wise convergence of the ![]() series almost everywhere on the unit circle. The special point, were the
series almost everywhere on the unit circle. The special point, were the
![]() series diverges, is easily identified as the point where
series diverges, is easily identified as the point where ![]() has a borderline hard singularity, since a single logarithmic integration
of
has a borderline hard singularity, since a single logarithmic integration
of ![]() will necessarily result in a soft singularity there.
will necessarily result in a soft singularity there.
If we extend the series ![]() to a full complex power series
to a full complex power series ![]() on
the unit disk, just as we did before in the case of
on
the unit disk, just as we did before in the case of ![]() and
and ![]() ,
we immediately see that
,
we immediately see that
Note that ![]() satisfies all the necessary conditions for convergence
to an inner analytic function. Since
satisfies all the necessary conditions for convergence
to an inner analytic function. Since ![]() converges to an analytic
function on the open unit disk and
converges to an analytic
function on the open unit disk and ![]() is analytic on the whole
complex plane, it follows that
is analytic on the whole
complex plane, it follows that ![]() also converges to an analytic
function on that disk. In addition to this, since
also converges to an analytic
function on that disk. In addition to this, since ![]() reduces to a
real function on the real line and
reduces to a
real function on the real line and ![]() reduces to a real function on
the real interval
reduces to a real function on
the real interval ![]() , so does
, so does ![]() . Finally, it is clear that
since
. Finally, it is clear that
since ![]() is zero at
is zero at ![]() , so is
, so is ![]() . Therefore
. Therefore ![]() converges
to an inner analytic function
converges
to an inner analytic function ![]() , so that we have
, so that we have
Since ![]() is absolutely and uniformly convergent on the unit circle,
the function
is absolutely and uniformly convergent on the unit circle,
the function ![]() can have only soft singularities on that circle.
However,
can have only soft singularities on that circle.
However, ![]() diverges to infinity at one point on the unit circle and,
due to the extended version of Abel's theorem [2], it follows
that
diverges to infinity at one point on the unit circle and,
due to the extended version of Abel's theorem [2], it follows
that ![]() must have a hard singularity at that point. We see therefore
that in this case the multiplication by
must have a hard singularity at that point. We see therefore
that in this case the multiplication by ![]() has the same effect of a
logarithmic integration. While the function
has the same effect of a
logarithmic integration. While the function ![]() has a single borderline
hard singularity at
has a single borderline
hard singularity at ![]() , the function
, the function ![]() has a borderline soft
singularity at that point.
has a borderline soft
singularity at that point.
We may conclude here that this whole class of series satisfies our
hypotheses defining a series of type ![]() in a regular
integral-differential chain, as well as that all of them converge almost
everywhere. Besides, all the series in this whole class have a single
dominant borderline hard singularity located at
in a regular
integral-differential chain, as well as that all of them converge almost
everywhere. Besides, all the series in this whole class have a single
dominant borderline hard singularity located at ![]() . Note that even if a
monotonic series has coefficients that go to zero as a power in ways other
than
. Note that even if a
monotonic series has coefficients that go to zero as a power in ways other
than ![]() with
with ![]() , the construction of
, the construction of ![]() still
applies. In this case
still
applies. In this case ![]() will still have a dominant singularity at
will still have a dominant singularity at
![]() , although no longer a borderline hard one, but a soft one instead.
, although no longer a borderline hard one, but a soft one instead.