Next: Factorization of Singularities Up: Monotonic Series Previous: A Monotonicity Test
The argument given in the last subsection can be generalized in several
ways, and the generalizations constitute proof of the convergence of wider
classes of series of type ![]() . For example, it can be trivially
generalized to series with negative
. For example, it can be trivially
generalized to series with negative ![]() for all
for all ![]() , converging to
zero from below. It is also trivial that it can be generalized to series
which include a non-monotonic initial part, up to some minimum value
, converging to
zero from below. It is also trivial that it can be generalized to series
which include a non-monotonic initial part, up to some minimum value
![]() of
of ![]() . In a less trivial, but still simple way, the argument can
be generalized to series with only odd-
. In a less trivial, but still simple way, the argument can
be generalized to series with only odd-![]() terms, such as the square wave,
or with only even-
terms, such as the square wave,
or with only even-![]() terms, such as the two-cycle sawtooth wave. We can
prove this in a simple way by reducing these cases to the previous one. If
we have a complex power series given by
terms, such as the two-cycle sawtooth wave. We can
prove this in a simple way by reducing these cases to the previous one. If
we have a complex power series given by
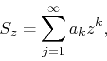
where ![]() , we may simply define new coefficients
, we may simply define new coefficients ![]() and a
new complex variable
and a
new complex variable ![]() , in terms of which the series can now be
written as
, in terms of which the series can now be
written as
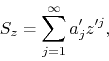
thus reducing it to the previous form, in terms of the variable ![]() . So
long as the non-zero coefficients
. So
long as the non-zero coefficients ![]() tend monotonically to zero as
tend monotonically to zero as
![]() , we have that the coefficients
, we have that the coefficients ![]() tend monotonically to
zero as
tend monotonically to
zero as ![]() , and the previous result applies. The same is true if
we have a complex power series given by
, and the previous result applies. The same is true if
we have a complex power series given by
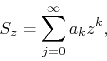
where ![]() , since we may still define new coefficients
, since we may still define new coefficients ![]() and the new complex variable
and the new complex variable ![]() , in terms of which the series can
now be written as
, in terms of which the series can
now be written as
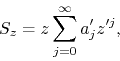
so that once more, so long as the non-zero coefficients tend monotonically
to zero, the previous result applies. We say that series such as these
have non-zero coefficients with a constant step ![]() . The only important
difference that comes up here is that the special points on the unit
circle are now defined by
. The only important
difference that comes up here is that the special points on the unit
circle are now defined by ![]() , which means that
, which means that ![]() and hence
that
and hence
that ![]() . Therefore, in these cases one gets two special points on
the unit circle, instead of one, namely
. Therefore, in these cases one gets two special points on
the unit circle, instead of one, namely ![]() and
and ![]() , at
which we have dominant singularities, which will be borderline hard
singularities so long as
, at
which we have dominant singularities, which will be borderline hard
singularities so long as
![]() with
with ![]() .
.
In addition to this, series with step ![]() and coefficients that have
alternating signs, such as
and coefficients that have
alternating signs, such as
![]() with monotonic
with monotonic ![]() ,
which are therefore not monotonic series, can be separated into two
sub-series with step
,
which are therefore not monotonic series, can be separated into two
sub-series with step ![]() , one with odd
, one with odd ![]() and the other with even
and the other with even ![]() ,
and since the coefficients of these two sub-series are monotonic, then the
result holds for each one of the two series, and hence for their sum. In
this case we will have two dominant singularities in each one of the
components series, located at
,
and since the coefficients of these two sub-series are monotonic, then the
result holds for each one of the two series, and hence for their sum. In
this case we will have two dominant singularities in each one of the
components series, located at ![]() . However, sometimes the two
singularities at
. However, sometimes the two
singularities at ![]() , one in each component series, may cancel off and
the original series may have a single dominant singularity located at
, one in each component series, may cancel off and
the original series may have a single dominant singularity located at
![]() . One can see this by means of a simple transformation of variables,
. One can see this by means of a simple transformation of variables,
where ![]() , so that
, so that ![]() implies
implies ![]() . Series with step
. Series with step ![]() and
coefficients that have alternating signs, such as
and
coefficients that have alternating signs, such as
![]() with
with ![]() or
or ![]() and monotonic
and monotonic ![]() , which are also not
monotonic themselves, can be separated into two sub-series with step
, which are also not
monotonic themselves, can be separated into two sub-series with step ![]() ,
and since the coefficients of these two sub-series are monotonic, then the
result holds for each one of the two series, and hence for their sum. In
this case we will have four dominant singularities in each one of the
components series, located at
,
and since the coefficients of these two sub-series are monotonic, then the
result holds for each one of the two series, and hence for their sum. In
this case we will have four dominant singularities in each one of the
components series, located at ![]() and
and
![]() . However, sometimes
the singularities at
. However, sometimes
the singularities at ![]() of the two component series may cancel off
and the original series may have only two dominant singularity located at
of the two component series may cancel off
and the original series may have only two dominant singularity located at
![]() . One can see this by means of another simple transformation of
variables,
. One can see this by means of another simple transformation of
variables,
where ![]() , so that
, so that ![]() implies
implies ![]() and hence
and hence
![]() .
In fact, the result can be generalized to series with non-zero terms only
at some arbitrary regular interval
.
In fact, the result can be generalized to series with non-zero terms only
at some arbitrary regular interval ![]() , that is, having non-zero
terms with some constant step other than
, that is, having non-zero
terms with some constant step other than ![]() . If we have a complex power
series given by
. If we have a complex power
series given by
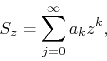
where ![]() , for some strictly positive integer
, for some strictly positive integer ![]() and where
the step
and where
the step ![]() is another strictly positive integer, we may simply define
new coefficients
is another strictly positive integer, we may simply define
new coefficients ![]() and a new complex variable
and a new complex variable ![]() , in
terms of which the series can now be written as
, in
terms of which the series can now be written as
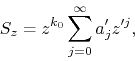
thus reducing it to the previous form, in terms of the variable ![]() . So
long as the non-zero coefficients
. So
long as the non-zero coefficients ![]() tend monotonically to zero as
tend monotonically to zero as
![]() , we have that the coefficients
, we have that the coefficients ![]() tend monotonically to
zero as
tend monotonically to
zero as ![]() , and the previous result applies. In this case the
special points over the unit circle are given by
, and the previous result applies. In this case the
special points over the unit circle are given by ![]() , and there are,
therefore,
, and there are,
therefore, ![]() such points, including
such points, including ![]() , uniformly distributed along
the circle. If combined with alternating signs, these series have special
points given by
, uniformly distributed along
the circle. If combined with alternating signs, these series have special
points given by ![]() , and once again there are
, and once again there are ![]() such points
uniformly distributed along the circle. Note that the number of dominant
singularities on the unit circle increases with the step
such points
uniformly distributed along the circle. Note that the number of dominant
singularities on the unit circle increases with the step ![]() , and that
they are homogeneously distributed along that circle.
, and that
they are homogeneously distributed along that circle.
Finally, one may consider building finite superpositions of the series in
all the previous cases discussed so far. Since each component series
converges almost everywhere and has a finite number of dominant
singularities, these superpositions of series will all converge, and will
all have a finite number of dominant singularities on the unit disk. Since
all the component series are of type ![]() , and hence have dominant
singularities which are borderline hard ones, the dominant singularities
of the superpositions will always be at most borderline hard ones. If the
dominant singularities are in fact borderline hard ones, then we will call
these series extended monotonic series. Each one of these series
generates a different regular integral-differential chain, and this
defines a rather large set of series that can be classified according to
our scheme, relating their mode of convergence and the dominant
singularities on the unit circle.
, and hence have dominant
singularities which are borderline hard ones, the dominant singularities
of the superpositions will always be at most borderline hard ones. If the
dominant singularities are in fact borderline hard ones, then we will call
these series extended monotonic series. Each one of these series
generates a different regular integral-differential chain, and this
defines a rather large set of series that can be classified according to
our scheme, relating their mode of convergence and the dominant
singularities on the unit circle.