Next: The Completeness Relation Up: Fourier Theory on the Previous: Fourier-Taylor Correspondence
The two most central elements of the structure of Fourier theory are the
set of orthogonality relations and the completeness relation. Let us then
show that these also follow from the structure of complex analysis. We
start with the orthogonality relations, which we already gave in
Equation (1) of the introduction. Of course the integrals
involved are simple ones, and can be calculated by elementary means. Our
objective here, however, is not to just calculate them but to show that
they are a consequence of the analytic structure of the complex plane. We
can do this by simply considering the Cauchy integral formulas for the
coefficients ![]() of the Taylor series of a simple power
of the Taylor series of a simple power ![]() , with
, with
![]() ,
,
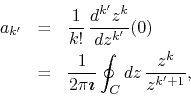
where ![]() is a circle or radius
is a circle or radius ![]() centered at the origin, with
centered at the origin, with
![]() . On the one hand, if
. On the one hand, if ![]() we get
we get ![]() due to the
multiple differentiation of the power function, which is differentiated
more times than the power itself. On the other hand, if
due to the
multiple differentiation of the power function, which is differentiated
more times than the power itself. On the other hand, if ![]() we get
we get
![]() when we calculate the derivatives and apply the result at zero,
since in this case there is always at least one factor of
when we calculate the derivatives and apply the result at zero,
since in this case there is always at least one factor of ![]() left, or
alternatively due to the Cauchy-Goursat theorem, because in this case the
integrand is analytic and thus the integral is zero. If
left, or
alternatively due to the Cauchy-Goursat theorem, because in this case the
integrand is analytic and thus the integral is zero. If ![]() , however,
we get
, however,
we get ![]() , which we can get either directly from the result of the
differentiation, or from the fact that in this case the integral is given
by
, which we can get either directly from the result of the
differentiation, or from the fact that in this case the integral is given
by
as one can easily verify, either directly or by the residues theorem. In any case we get the result
We now write the integral explicitly on the circle of radius ![]() , using
, using
![]() as the integration variable, with
as the integration variable, with
![]() and
thus with
and
thus with
![]() ,
,
![\begin{eqnarray*}
\delta_{kk'}
& = &
\frac{1}{2\pi\mbox{\boldmath$\imath$}}
...
...\pi}d\theta\,
\cos(k\theta)
\sin(k'\theta)
\right]
\right\}.
\end{eqnarray*}](img116.png)
One can see that the integrals in the imaginary part are zero due to parity arguments. In fact, these constitute some of the orthogonality relations, those including sines and cosines. We are left with
For ![]() the second term vanishes, and the equation becomes a simple
identity, which is in fact one of the other orthogonality relations. If,
on the other hand, we have
the second term vanishes, and the equation becomes a simple
identity, which is in fact one of the other orthogonality relations. If,
on the other hand, we have ![]() , we now consider the integral, on the
same circuit,
, we now consider the integral, on the
same circuit,
which is zero due to the Cauchy-Goursat theorem, since the integrand is
analytic within the circle ![]() for
for ![]() . Writing the integral
explicitly on the circle we get
. Writing the integral
explicitly on the circle we get
![\begin{eqnarray*}
0
& = &
\int_{-\pi}^{\pi}d\theta\,
\mbox{\boldmath$\imath$...
...\pi}d\theta\,
\cos(k\theta)
\sin(k'\theta)
\right]
\right\}.
\end{eqnarray*}](img122.png)
Once again the integrals in the imaginary part are zero by parity arguments, and thus we are left with
since ![]() . If we now go back to our previous expression in
Equation (4) we see that the two integrals that appear there
are equal to each other, so we may write that
. If we now go back to our previous expression in
Equation (4) we see that the two integrals that appear there
are equal to each other, so we may write that
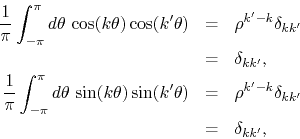
where the factor involving ![]() is irrelevant since the right-hand sides
are only different from zero if
is irrelevant since the right-hand sides
are only different from zero if ![]() . We get therefore the complete set
of orthogonality relations
. We get therefore the complete set
of orthogonality relations
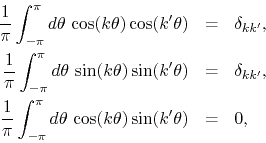
for ![]() and
and ![]() , which are the relevant values for DP Fourier
series. It is interesting to note that the orthogonality relations are
valid on the circle of radius
, which are the relevant values for DP Fourier
series. It is interesting to note that the orthogonality relations are
valid on the circle of radius ![]() with
with ![]() , without the need
to actually take the
, without the need
to actually take the ![]() limit. We thus get a bit more than we
bargained for in this case, for it would have been sufficient to establish
these relation only on the unit circle. Note that this is different from
what happened during the calculation of the coefficients of the Fourier
series. However, in both cases the results come from the Cauchy integral
formulas and the Cauchy-Goursat theorem, and in either case the same real
integral appears, defining the usual scalar product in the space of real
functions on the periodic interval.
limit. We thus get a bit more than we
bargained for in this case, for it would have been sufficient to establish
these relation only on the unit circle. Note that this is different from
what happened during the calculation of the coefficients of the Fourier
series. However, in both cases the results come from the Cauchy integral
formulas and the Cauchy-Goursat theorem, and in either case the same real
integral appears, defining the usual scalar product in the space of real
functions on the periodic interval.