Next: Limits from Within Up: Fourier Theory on the Previous: The Orthogonality Relations
Let us now show that the completeness relation of the Fourier basis also
follows from the structure of complex analysis. In order to do this, we
must first show that the Dirac delta ``function'' can be represented in
terms of the analytic structure within the open unit disk. We denote the
Dirac delta ``function'' centered at
![]() on the unit
circle by
on the unit
circle by
![]() . The definition of this mathematical
object is that it is a symbolic representation of a limiting process which
has the following four properties:
. The definition of this mathematical
object is that it is a symbolic representation of a limiting process which
has the following four properties:
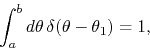
has the value shown, for any interval ![]() which contains the point
which contains the point
![]() ;
;
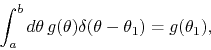
has the value shown, for any interval ![]() which contains the point
which contains the point
![]() .
.
Of course no real function exists that can have all these properties, which justifies the quotes in which we wrap the word ``function'' when referring to it. In order to construct the Dirac delta ``function'' we must first give an object or set of objects over which the limiting process can be defined, and then define that limiting process. In order to fulfill this program, we consider the complex function given within the open unit disk by
as well as its restrictions to circles of radius ![]() centered at the
origin, with
centered at the
origin, with ![]() , where
, where
![]() and where
and where
![]() is a point on the unit circle. This function
is analytic within the open unit disk, but it is not an inner analytic
function, because
is a point on the unit circle. This function
is analytic within the open unit disk, but it is not an inner analytic
function, because ![]() is not zero. However, we may write it in
terms of another function
is not zero. However, we may write it in
terms of another function ![]() as
as
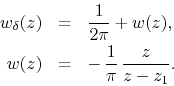
Strictly speaking, ![]() is not an inner analytic function either,
because it does not reduce to a real function over the real axis. However,
it does reduce to a real function over the straight line
is not an inner analytic function either,
because it does not reduce to a real function over the real axis. However,
it does reduce to a real function over the straight line ![]() ,
with real
,
with real ![]() , since in this case we have
, since in this case we have
We see therefore that ![]() is an inner analytic function rotated around
the origin by the angle
is an inner analytic function rotated around
the origin by the angle ![]() associated to
associated to ![]() . Therefore this
is just a simple extension of the structure we defined here. The limiting
process to be used for the definition is just the
. Therefore this
is just a simple extension of the structure we defined here. The limiting
process to be used for the definition is just the ![]() limit to the
unit circle. We will now show that the real part of
limit to the
unit circle. We will now show that the real part of ![]() , taken
on the
, taken
on the ![]() limit, satisfies all the required properties defining
the Dirac delta ``function''. In order to recover the real and imaginary
parts of this complex function, we must now rationalize it,
limit, satisfies all the required properties defining
the Dirac delta ``function''. In order to recover the real and imaginary
parts of this complex function, we must now rationalize it,
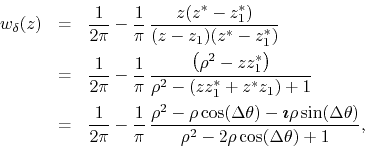
where
![]() . We now examine the real part of
this function,
. We now examine the real part of
this function,
If we now take the limit ![]() , under the assumption that
, under the assumption that
![]() , we get
, we get
![\begin{eqnarray*}
\lim_{\rho\to 1}\Re[w_{\delta}(z)]
& = &
\frac{1}{2\pi}
-
...
...}
\\
& = &
\frac{1}{2\pi}
-
\frac{1}{2\pi}
\\
& = &
0,
\end{eqnarray*}](img149.png)
which is the correct value for the case of the Dirac delta ``function''. Thus we see that the first property holds.
If, on the other hand, we calculate
![]() for
for
![]() and
and ![]() we obtain
we obtain
![\begin{eqnarray*}
\Re[w_{\delta}(z)]
& = &
\frac{1}{2\pi}
-
\frac{1}{\pi}\,...
... & = &
\frac{1}{2\pi}
-
\frac{1}{\pi}\,
\frac{\rho}{\rho-1},
\end{eqnarray*}](img153.png)
which diverges to positive infinity as ![]() from below, as it
should in order to represent the singular Dirac delta ``function''. This
establishes that the second property holds.
from below, as it
should in order to represent the singular Dirac delta ``function''. This
establishes that the second property holds.
We then calculate the integral of
![]() over the circle of
radius
over the circle of
radius ![]() , which is given by
, which is given by
![\begin{eqnarray*}
I_{1}
& = &
\frac{1}{2\pi}
\int_{-\pi}^{\pi}d\theta\,
\rh...
...left[\left(\rho^{2}+1\right)/(2\rho)\right]-\cos(\Delta\theta)},
\end{eqnarray*}](img154.png)
since
![]() . Note that this is not the integral
of an analytic function over a closed contour, but the integral of a real
function over the circle of radius
. Note that this is not the integral
of an analytic function over a closed contour, but the integral of a real
function over the circle of radius ![]() . This real integral over
. This real integral over
![]() can be calculated by residues. We introduce an auxiliary complex
variable
can be calculated by residues. We introduce an auxiliary complex
variable
![]() , which becomes simply
, which becomes simply
![]() on the unit circle
on the unit circle ![]() . We have
. We have
![]() , and so we may write the integral as
, and so we may write the integral as
![\begin{eqnarray*}
\int_{-\pi}^{\pi}d(\Delta\theta)\,
\frac{1}{\left[\left(1+\r...
...frac{1}{1-\left[\left(1+\rho^{2}\right)/\rho\right]\xi+\xi^{2}},
\end{eqnarray*}](img160.png)
where the integral is now over the unit circle ![]() in the complex
in the complex ![]() plane. The two roots of the quadratic polynomial on
plane. The two roots of the quadratic polynomial on ![]() in the
denominator are given by
in the
denominator are given by
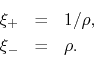
Since ![]() , only the pole corresponding to
, only the pole corresponding to ![]() lies inside the
integration contour, so we get for the integral
lies inside the
integration contour, so we get for the integral
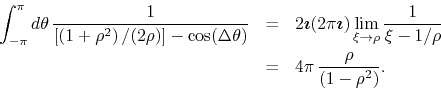
It follows that we have for the integral ![]()
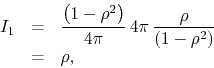
so that we have ![]() in the
in the ![]() limit. Once we have this
result, and since the integrand goes to zero everywhere on the unit circle
except at
limit. Once we have this
result, and since the integrand goes to zero everywhere on the unit circle
except at
![]() , which means that
, which means that
![]() , the
integral can be changed to one over any open interval on the unit circle
containing the point
, the
integral can be changed to one over any open interval on the unit circle
containing the point ![]() , without any change in its limiting
value. This establishes that the third property holds.
, without any change in its limiting
value. This establishes that the third property holds.
In order to establish the fourth and last property, we take an essentially
arbitrary inner analytic function ![]() , with the single additional
restriction that it be well-defined at the point
, with the single additional
restriction that it be well-defined at the point ![]() , in the sense
that its
, in the sense
that its ![]() limit exists at
limit exists at ![]() . This inner analytic function
corresponds to a pair of FC real functions on the unit circle, both of
which are well-defined at
. This inner analytic function
corresponds to a pair of FC real functions on the unit circle, both of
which are well-defined at ![]() . We now consider the following integral
over the circle of radius
. We now consider the following integral
over the circle of radius ![]() ,
,
![\begin{eqnarray*}
I_{2}
& = &
\frac{1}{2\pi}
\int_{-\pi}^{\pi}d\theta\,
\rh...
...left[\left(\rho^{2}+1\right)/(2\rho)\right]-\cos(\Delta\theta)},
\end{eqnarray*}](img169.png)
since
![]() . Note once more that this is not the
integral of an analytic function over a closed contour, but two integrals
of real functions, given by the real and imaginary parts of
. Note once more that this is not the
integral of an analytic function over a closed contour, but two integrals
of real functions, given by the real and imaginary parts of ![]() ,
over the circle of radius
,
over the circle of radius ![]() . These real integrals over
. These real integrals over ![]() can
be calculated by residues, exactly like the one which appeared before in
the case of
can
be calculated by residues, exactly like the one which appeared before in
the case of ![]() . The calculation is exactly the same except for the
extra factor of
. The calculation is exactly the same except for the
extra factor of ![]() to be taken into consideration when
calculating the residue, so that we may write directly that
to be taken into consideration when
calculating the residue, so that we may write directly that
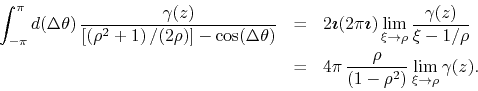
Note now that since
![]() and we must take
the limit
and we must take
the limit ![]() , we in fact have that in that limit
, we in fact have that in that limit
which implies that ![]() and that
and that
![]() . We must
therefore write
. We must
therefore write ![]() at the point given by
at the point given by ![]() and
and
![]() , that is, at the point given by
, that is, at the point given by ![]() and
and ![]() ,
,
It follows that we have for the integral ![]()
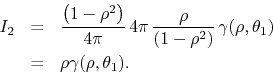
Finally, we may now take the ![]() limit, since
limit, since
![]() is well-defined in that limit, and thus obtain
is well-defined in that limit, and thus obtain
Once we have this result, and since the integrand goes to zero everywhere
on the unit circle except at
![]() , which means that
, which means that
![]() , the integral can be changed to one over any open
interval on the unit circle containing the point
, the integral can be changed to one over any open
interval on the unit circle containing the point ![]() , without any
change in its value. This establishes that the fourth and last property
holds. We may then write symbolically that
, without any
change in its value. This establishes that the fourth and last property
holds. We may then write symbolically that
Note that in order to obtain this result it was not necessary to assume
that ![]() is continuous at
is continuous at ![]() in the direction of
in the direction of ![]() along the unit circle. It was necessary to assume only that
along the unit circle. It was necessary to assume only that ![]() is
continuous as a function of
is
continuous as a function of ![]() , in the direction perpendicular to the
unit circle. One can see therefore that, once more, we get a bit more than
we bargained for, because we were able to establish the result with
slightly weaker hypotheses than at first expected.
, in the direction perpendicular to the
unit circle. One can see therefore that, once more, we get a bit more than
we bargained for, because we were able to establish the result with
slightly weaker hypotheses than at first expected.
We are now in a position to establish the completeness relation using this
representation of the Dirac delta ``function''. If we use once again the
Cauchy integral formulas for ![]() we get for the coefficients of the
Taylor expansion of
we get for the coefficients of the
Taylor expansion of ![]()
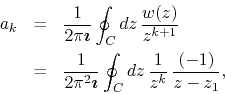
for ![]() , since
, since ![]() is a rotated inner analytic function. We now
observe that the second ratio in the integrand can be understood as the
sum of a geometric series, which is convergent so long as
is a rotated inner analytic function. We now
observe that the second ratio in the integrand can be understood as the
sum of a geometric series, which is convergent so long as ![]() ,
,
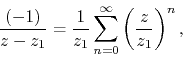
so that we may now write
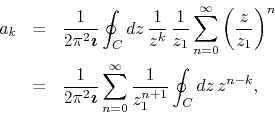
since a convergent power series can always be integrated term-by-term. As
we have already discussed before, in the previous section, the remaining
integral is zero except if ![]() , in which case it has the value
, in which case it has the value
![]() . Note that this condition relating
. Note that this condition relating ![]() and
and ![]() can always be
satisfied since
can always be
satisfied since ![]() . We therefore get for the coefficients
. We therefore get for the coefficients
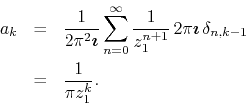
As a result, we get for the Taylor expansion of ![]()
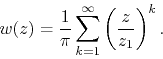
We now write both ![]() and
and ![]() in polar coordinates, to obtain
in polar coordinates, to obtain
![\begin{eqnarray*}
w(z)
& = &
\frac{1}{\pi}
\sum_{k=1}^{\infty}
\rho^{k}
\,...
...k\theta)
\sin(k\theta_{1})
\right]
\rule{0em}{3ex}
\right\}.
\end{eqnarray*}](img188.png)
If we now write the real part of ![]() we get
we get
![\begin{displaymath}
\Re[w_{\delta}(z)]
=
\frac{1}{2\pi}
+
\frac{1}{\pi}
\s...
...os(k\theta_{1})
+
\sin(k\theta)
\sin(k\theta_{1})
\right],
\end{displaymath}](img189.png)
and, if we then take the ![]() limit, we get the expression
limit, we get the expression
![\begin{displaymath}
\delta(\theta-\theta_{1})
=
\frac{1}{2\pi}
+
\frac{1}{\...
...os(k\theta_{1})
+
\sin(k\theta)
\sin(k\theta_{1})
\right],
\end{displaymath}](img190.png)
which is the completeness relation in its usual form, a bilinear form on
the Fourier basis functions, at two separate points along the unit circle.
Note that the constant function, which is an element of the complete
Fourier basis, is included in the first term. Note also that this time it
was necessary to take the ![]() limit, and that the completeness of
the Fourier basis is valid only on the unit circle. This is to be
expected, of course, since the unit circle is where the corresponding
space of real functions, which is generated by the basis, is defined.
limit, and that the completeness of
the Fourier basis is valid only on the unit circle. This is to be
expected, of course, since the unit circle is where the corresponding
space of real functions, which is generated by the basis, is defined.