Next: Trigonometric Series on the Up: Fourier Theory on the Previous: Fourier Theory on the
In this paper we will establish an interesting relation between Fourier series and analytic functions. This leads to an alternative way to deal with Fourier series and to characterize the corresponding real functions. This relation will allow us to discuss the convergence of Fourier series in terms of the convergence of the Taylor series of analytic functions. The convergence issues will be developed up to a certain point, and further developments will be discussed in a follow-up paper [1]. This relation will also give us an alternative way to recover, from the coefficients of the series, the functions that originated them, which works even if the Fourier series are divergent. Perhaps most importantly, it will provide a different and possibly richer point of view for Fourier series and the corresponding real functions.
We will use repeatedly the following very well-known and fundamental
theorem of complex analysis, about complex power series [2].
If we consider the general complex power series written around the origin
![]() ,
,
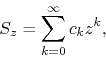
where
![]() is a complex variable and
is a complex variable and ![]() are arbitrary complex
constants, then the following holds. If
are arbitrary complex
constants, then the following holds. If ![]() converges at a point
converges at a point
![]() , then it is convergent and absolutely convergent on an open
disk centered at
, then it is convergent and absolutely convergent on an open
disk centered at ![]() with its boundary passing through
with its boundary passing through ![]() . In
addition to this, it converges uniformly on any closed set contained
within this open disk. We will refer to this state of affairs in what
regards convergence as strong convergence, and will refer to this
theorem as the basic convergence theorem. Furthermore, the power
series converges to an analytic function of which it is the Taylor series
around
. In
addition to this, it converges uniformly on any closed set contained
within this open disk. We will refer to this state of affairs in what
regards convergence as strong convergence, and will refer to this
theorem as the basic convergence theorem. Furthermore, the power
series converges to an analytic function of which it is the Taylor series
around ![]() .
.
We will make a conceptual distinction between trigonometric series and
Fourier series. An arbitrary real trigonometric series on the real
variable ![]() with domain in the periodic interval
with domain in the periodic interval ![]() is
given by
is
given by
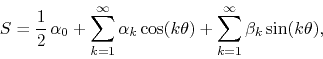
where ![]() and
and ![]() are any real numbers. If there is a
real function
are any real numbers. If there is a
real function ![]() such that the coefficients
such that the coefficients ![]() and
and
![]() are given in terms of that function by the integrals
are given in terms of that function by the integrals
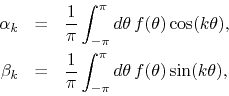
then we call this series the Fourier series of that
function [3]. Since the Fourier coefficients are defined by
means of integrals, it is clear that one can add to ![]() any
zero-measure function without modifying them. This means that a convergent
Fourier series can only be said to converge almost everywhere to the
function which originated it, that is, with the possible exclusion of a
zero-measure subset of the domain.
any
zero-measure function without modifying them. This means that a convergent
Fourier series can only be said to converge almost everywhere to the
function which originated it, that is, with the possible exclusion of a
zero-measure subset of the domain.
With this limitation, the Fourier basis in the space of real functions on
the periodic interval, formed by the constant function, the set of
functions ![]() , with
, with
![]() , and the set of
functions
, and the set of
functions ![]() , with
, with
![]() , is complete to
generate all sufficiently well-behaved functions in that interval. With
the exclusion of the constant function, the remaining basis generates the
set of all sufficiently well-behaved zero-average real functions. The
remaining basis functions satisfy the orthogonality relations
, is complete to
generate all sufficiently well-behaved functions in that interval. With
the exclusion of the constant function, the remaining basis generates the
set of all sufficiently well-behaved zero-average real functions. The
remaining basis functions satisfy the orthogonality relations
for ![]() and
and ![]() . In a stricter sense, the
good-behavior conditions on the real functions are that they be integrable
and that they be such that their Fourier series converge. However, one
might consider the set of coefficients themselves to be sufficient to
characterize the function that originated them, even if the series does
not converge. This makes full sense if there is an alternative way to
recover the functions from the coefficients of their series, such as the
one we will present in this paper, which is not dependent on the
convergence of the series. In this case the condition of integrability
suffices. The important point to be kept in mind here is that the set of
coefficients determines the function uniquely almost everywhere over the
periodic interval.
. In a stricter sense, the
good-behavior conditions on the real functions are that they be integrable
and that they be such that their Fourier series converge. However, one
might consider the set of coefficients themselves to be sufficient to
characterize the function that originated them, even if the series does
not converge. This makes full sense if there is an alternative way to
recover the functions from the coefficients of their series, such as the
one we will present in this paper, which is not dependent on the
convergence of the series. In this case the condition of integrability
suffices. The important point to be kept in mind here is that the set of
coefficients determines the function uniquely almost everywhere over the
periodic interval.
The parity of the real functions will play an important role in this
paper. Any real function defined in a symmetric domain around zero,
without any additional hypotheses, can be separated into its even and odd
parts. An even function is one that satisfies the condition
![]() , while an odd one satisfies the condition
, while an odd one satisfies the condition
![]() . For any real function we can write that
. For any real function we can write that
![]() , with
, with
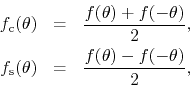
where
![]() is even and
is even and
![]() is odd. The
Fourier basis can also be separated into even and odd parts. Since the
constant function and the cosines are even, they generate the even parts
of the real functions, while the sines, being odd, generate the odd parts.
Since the set of cosines and the set of sines are two independent and
mutually orthogonal sets of functions, the convergence of the
trigonometric series can only be accomplished by the separate convergence
of the cosine sub-series and the sine sub-series, which we denote by
is odd. The
Fourier basis can also be separated into even and odd parts. Since the
constant function and the cosines are even, they generate the even parts
of the real functions, while the sines, being odd, generate the odd parts.
Since the set of cosines and the set of sines are two independent and
mutually orthogonal sets of functions, the convergence of the
trigonometric series can only be accomplished by the separate convergence
of the cosine sub-series and the sine sub-series, which we denote by
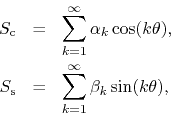
so that
![]() . For simplicity, in this
paper we will consider only series in which
. For simplicity, in this
paper we will consider only series in which ![]() , which
correspond to functions
, which
correspond to functions ![]() that have zero average over the
periodic interval. There is of course no loss of generality involved in
doing this, since the addition of a constant term is a trivial procedure
that does not bear on the convergence issues. The discussion of the
convergence of arbitrary trigonometric series
that have zero average over the
periodic interval. There is of course no loss of generality involved in
doing this, since the addition of a constant term is a trivial procedure
that does not bear on the convergence issues. The discussion of the
convergence of arbitrary trigonometric series ![]() is therefore equivalent
to the separate discussion of the convergence of arbitrary cosine series
is therefore equivalent
to the separate discussion of the convergence of arbitrary cosine series
![]() and arbitrary sine series
and arbitrary sine series ![]() . These last two classes
consist of trigonometric series with definite parities and we will name
them Definite-Parity trigonometric series, or DP trigonometric
series for short.
. These last two classes
consist of trigonometric series with definite parities and we will name
them Definite-Parity trigonometric series, or DP trigonometric
series for short.
A note about the fact that we limit ourselves to real Fourier series here.
We might as well consider the series ![]() with complex coefficients
with complex coefficients
![]() and
and ![]() , but due to the linearity of the series with
respect to these coefficients, any such complex Fourier series would at
once decouple into two real Fourier series, one in the real part and one
in the imaginary part, and would therefore reduce the discussion to the
one we choose to develop here. Therefore nothing fundamentally new is
introduced by the examination of complex Fourier series, and it is enough
to limit the discussion to the real case.
, but due to the linearity of the series with
respect to these coefficients, any such complex Fourier series would at
once decouple into two real Fourier series, one in the real part and one
in the imaginary part, and would therefore reduce the discussion to the
one we choose to develop here. Therefore nothing fundamentally new is
introduced by the examination of complex Fourier series, and it is enough
to limit the discussion to the real case.