Trigonometric Series on the Complex Plane

First of all, let us establish a very basic correspondence between real trigonometric series and power series in the complex plane. In this section we do not assume that the trigonometric series are Fourier series. In fact, for the time being we impose no additional restrictions on the numbers $\alpha_{k}$ and $\beta_{k}$, other than that they be real, and in particular we do not assume anything about the convergence of the series.

Consider then an arbitrary DP trigonometric series. We now introduce a useful definition. Given a cosine series $S_{\rm c}$ with coefficients $\alpha_{k}$, we will define from it a corresponding sine series by

$$\bar{S}_{\rm c} = \sum_{k=1}^{\infty} \alpha_{k}\sin(k\theta).$$

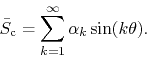
We will call this new trigonometric series the Fourier-Conjugate series to $S_{\rm c}$, or the FC series for short. Note that $\bar{S}_{\rm c}$ is odd instead of even. Similarly, given a sine series $S_{\rm s}$ with coefficients $\beta_{k}$, we will define from it a corresponding cosine series by

$$\bar{S}_{\rm s} = \sum_{k=1}^{\infty} \beta_{k}\cos(k\theta),$$

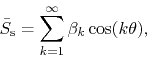
which we will also name the Fourier-Conjugate series to $S_{\rm s}$. Note that $\bar{S}_{\rm s}$ is even instead of odd. We see therefore that the set of all DP trigonometric series can be organized in pairs of mutually conjugate series. In any given pair, each series is the FC series of the other.

From now on we will denote all trigonometric series coefficients by $a_{k}$, regardless of whether the series originally under discussion is a cosine series or a sine series. Now, given any cosine series $S_{\rm c}$ or any sine series $S_{\rm s}$, we may define from it a complex series $S_{v}$ by the use of the original series and its FC series as the real and imaginary parts of the complex series. In the case of an original cosine series we thus define

$$S_{v} = S_{\rm c} + \mbox{\boldmath$\imath$} \bar{S}_{\rm c},$$

while in the case of an original sine series we define

$$S_{v} = \bar{S}_{\rm s} + \mbox{\boldmath$\imath$} S_{\rm s}.$$

In this way the discussion of the convergence of arbitrary DP trigonometric series can be reduced to the discussion of the convergence of the corresponding complex series $S_{v}$. In either one of the two cases above this series may be written as

$$\begin{eqnarray*} S_{v} & = & \sum_{k=1}^{\infty} a_{k}\cos(k\theta) + \mb... ...s(k\theta) + \mbox{\boldmath$\imath$} \sin(k\theta) \right], \end{eqnarray*}$$

where the coefficients $a_{k}$ are still completely arbitrary. If we now define the complex variable $v=\exp(\mbox{\boldmath$\imath$}\theta)$, then using Euler's formula we may write this complex series as

$$S_{v} = \sum_{k=1}^{\infty} a_{k}v^{k},$$

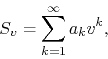
so that it becomes, therefore, a complex power series with real coefficients on the unit circle centered at the origin, in the complex plane. Finally, we may look at this series as a restriction to the unit circle of a full power series on the complex plane if we introduce an extra real variable $\rho\geq 0$, so that a complex variable

$$\begin{eqnarray*} z & = & \rho v \\ & = & \rho\,{\rm e}^{\mbox{\boldmath$\imath$}\theta} \end{eqnarray*}$$

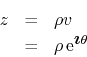
can be defined over the whole complex plane, and consider the complex power series, still with real coefficients,

$$S_{z} = \sum_{k=1}^{\infty} a_{k}z^{k}.$$

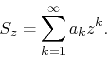
This is a complex power series centered at $z=0$, with no $k=0$ term, so that is assumes the value zero at $z=0$. Apart from the fact that $a_{0}=0$, it has real but otherwise arbitrary coefficients. The series $S_{v}$ that we constructed from a pair of FC trigonometric series is just $S_{z}$ restricted to $\rho=1$, for $\theta\in[-\pi,\pi]$. In other words, the series $S_{v}$ is a restriction to the unit circle of the complex power series we just defined. There is, therefore, a one-to-one correspondence between pairs of mutually FC trigonometric series and complex power series around $z=0$ with real coefficients and $a_{0}=0$.

We thus establish that the discussion of the convergence of arbitrary DP trigonometric series can be reduced to the discussion of the convergence of the corresponding complex power series $S_{z}$ on the unit circle. In fact, the whole question of the convergence of trigonometric series is revealed to be identical to the question of the convergence of complex power series on the boundary of the unit disk, including the cases in which that disk is the maximum disk of convergence of the power series.