Next: Fourier-Taylor Correspondence Up: Fourier Theory on the Previous: Trigonometric Series on the
Let us now show that the usual formulas giving the Fourier coefficients,
in terms of integrals involving the corresponding real functions, follow
as consequences of the analytic properties of certain complex functions
within the open unit disk. In order to do this, let us consider a pair of
FC trigonometric series that have the rather weak property that there is
at least one value of ![]() for which both elements of the pair are
convergent. Note that this constitutes an indirect restriction on the
coefficients of the series. It follows at once that the power series
for which both elements of the pair are
convergent. Note that this constitutes an indirect restriction on the
coefficients of the series. It follows at once that the power series
![]() converges at the point on the unit circle that corresponds to that
value of
converges at the point on the unit circle that corresponds to that
value of ![]() . Consequently, it follows from the basic convergence
theorem that the power series is strongly convergent at least on the open
unit disk. Furthermore, it converges to a complex function that is
analytic at least on the open unit disk, which we will denote by
. Consequently, it follows from the basic convergence
theorem that the power series is strongly convergent at least on the open
unit disk. Furthermore, it converges to a complex function that is
analytic at least on the open unit disk, which we will denote by ![]() ,
and therefore we may now write
,
and therefore we may now write
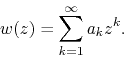
Note that, since the coefficients are real, the function ![]() reduces to
a purely real function on the open interval
reduces to
a purely real function on the open interval ![]() of the real axis. It
is therefore the analytic continuation of a real analytic function defined
on that interval. Apart from this fact, from the fact that
of the real axis. It
is therefore the analytic continuation of a real analytic function defined
on that interval. Apart from this fact, from the fact that ![]() , and
from the fact that it is analytic on the open unit disk, it is an
otherwise arbitrary analytic function. In addition to all this, we have
that
, and
from the fact that it is analytic on the open unit disk, it is an
otherwise arbitrary analytic function. In addition to all this, we have
that ![]() is the Taylor series of
is the Taylor series of ![]() around
around ![]() . We will call an
analytic function that has these properties an inner analytic
function. Let us list the defining properties. An inner analytic
function is one that:
. We will call an
analytic function that has these properties an inner analytic
function. Let us list the defining properties. An inner analytic
function is one that:
Let us now examine another property of ![]() implied by the fact that it
is the analytic continuation of a real function. If we use polar
coordinates and write
implied by the fact that it
is the analytic continuation of a real function. If we use polar
coordinates and write
![]() , with
, with
![]() ,
then we may write out the Taylor series of
,
then we may write out the Taylor series of ![]() as
as
![\begin{displaymath}
w(z)
=
\sum_{k=1}^{\infty}
a_{k}\rho^{k}
\left[
\cos(k\theta)
+
\mbox{\boldmath$\imath$}
\sin(k\theta)
\right].
\end{displaymath}](img63.png)
Since the coefficients are real, we have at once that
![\begin{displaymath}
w(z)
=
\left[
\,
\sum_{k=1}^{\infty}
a_{k}\rho^{k}
\c...
...,
\sum_{k=1}^{\infty}
a_{k}\rho^{k}
\sin(k\theta)
\right],
\end{displaymath}](img64.png)
where the expressions within square brackets are real. If we write ![]() in terms of its real and imaginary parts,
in terms of its real and imaginary parts,
then the real part
![]() must be even on
must be even on ![]() ,
because it is the function that the cosine series contained in
,
because it is the function that the cosine series contained in ![]() converges to,
converges to,
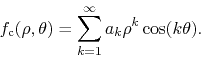
Similarly, the imaginary part
![]() must be odd on
must be odd on
![]() , because it is the function that the sine series contained in
, because it is the function that the sine series contained in
![]() converges to,
converges to,
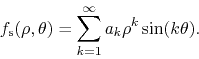
With these preliminaries established, we may now proceed towards our
objective here, which consists of the inversion of the relations above, so
that we may write ![]() in terms of
in terms of
![]() , or in
terms of
, or in
terms of
![]() , by means of the use of the analytic
structure within the open unit disk. Consider then the Cauchy integral
formulas for the function
, by means of the use of the analytic
structure within the open unit disk. Consider then the Cauchy integral
formulas for the function ![]() and its derivatives, written around
and its derivatives, written around ![]() for the
for the ![]() derivative,
derivative,
where ![]() is the circle centered at
is the circle centered at ![]() with radius
with radius ![]() . The
coefficients of the Taylor series of
. The
coefficients of the Taylor series of ![]() may be written in terms of
these integrals, so that we have for
may be written in terms of
these integrals, so that we have for ![]()
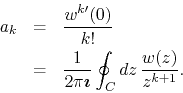
It is very important to note that since ![]() is analytic in the open
unit disk, by the Cauchy-Goursat theorem the integral is independent of
is analytic in the open
unit disk, by the Cauchy-Goursat theorem the integral is independent of
![]() within that disk, and therefore so are the coefficients
within that disk, and therefore so are the coefficients ![]() .
We now write the integral explicitly, using the integration variable
.
We now write the integral explicitly, using the integration variable
![]() on the circle of radius
on the circle of radius ![]() . We have
. We have
![]() , and therefore get
, and therefore get
![\begin{eqnarray*}
a_{k}
& = &
\frac{1}{2\pi\mbox{\boldmath$\imath$}}
\int_{-...
...ho,\theta)
\sin(k\theta)
\right]
\rule{0em}{2.5ex}
\right\}.
\end{eqnarray*}](img77.png)
Since we know that ![]() are real, we may at once conclude that the
imaginary part of this last integral is zero. But we can state more than
just that, because all the functions appearing in all these integrals have
definite parities on
are real, we may at once conclude that the
imaginary part of this last integral is zero. But we can state more than
just that, because all the functions appearing in all these integrals have
definite parities on ![]() , and hence we see that the integrands that
appear in the imaginary part are odd, while the integrals are over
symmetric intervals. We therefore conclude that the following two
integrals are separately zero,
, and hence we see that the integrands that
appear in the imaginary part are odd, while the integrals are over
symmetric intervals. We therefore conclude that the following two
integrals are separately zero,
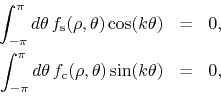
for all ![]() . We are therefore left with the following expression for
. We are therefore left with the following expression for
![]() ,
,
In order to continue the analysis of the coefficients ![]() we consider
now the following integral on the same circuit
we consider
now the following integral on the same circuit ![]() ,
,
with ![]() . The integral is zero by the Cauchy-Goursat theorem, since for
. The integral is zero by the Cauchy-Goursat theorem, since for
![]() the integrand is analytic on the open unit disk. As before we write
the integral on the circle of radius
the integrand is analytic on the open unit disk. As before we write
the integral on the circle of radius ![]() using the integration variable
using the integration variable
![]() , to get
, to get
![\begin{eqnarray*}
0
& = &
\int_{-\pi}^{\pi}d\theta\,
\mbox{\boldmath$\imath$...
...ho,\theta)
\sin(k\theta)
\right]
\rule{0em}{2.5ex}
\right\}.
\end{eqnarray*}](img82.png)
Once again the integrals that appear in the imaginary part of this last
expression are zero by parity arguments, and since ![]() we are
left with
we are
left with
which is valid for all ![]() . We conclude therefore that the two integrals
shown are equal,
. We conclude therefore that the two integrals
shown are equal,
for all ![]() . If we now go back to the expression in
Equation (2) for
. If we now go back to the expression in
Equation (2) for ![]() we see that the two integrals
appearing in that expression are equal to each other. We may therefore
write for the coefficients
we see that the two integrals
appearing in that expression are equal to each other. We may therefore
write for the coefficients
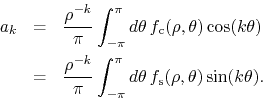
We observe now that these formulas for the coefficients ![]() are simple
extensions of the usual formulas for the Fourier coefficients of the even
function
are simple
extensions of the usual formulas for the Fourier coefficients of the even
function
![]() and the odd function
and the odd function
![]() , and therefore are related in a simple way to the
Fourier coefficients for the real function of
, and therefore are related in a simple way to the
Fourier coefficients for the real function of ![]()
with ![]() interpreted as an extra parameter. In fact, these formulas
become the usual ones in the
interpreted as an extra parameter. In fact, these formulas
become the usual ones in the ![]() limit, thus completing the
construction of a pair of FC Fourier series on the unit circle.
limit, thus completing the
construction of a pair of FC Fourier series on the unit circle.
Whether or not we may now take the limit ![]() in these formulas
depends on whether or not the coefficients, and hence the integrals that
define them, are continuous functions of
in these formulas
depends on whether or not the coefficients, and hence the integrals that
define them, are continuous functions of ![]() at the unit circle, for
limits coming from within the unit disk. We saw before that the
coefficients are constant with
at the unit circle, for
limits coming from within the unit disk. We saw before that the
coefficients are constant with ![]() , and therefore are continuous
functions of
, and therefore are continuous
functions of ![]() within the open unit disk. We therefore know that
their
within the open unit disk. We therefore know that
their ![]() limits exist. Furthermore, by construction these are the
coefficients of the FC pair of DP trigonometric series we started with, on
the unit circle. Therefore the coefficients assume at
limits exist. Furthermore, by construction these are the
coefficients of the FC pair of DP trigonometric series we started with, on
the unit circle. Therefore the coefficients assume at ![]() the values
given by their limits when
the values
given by their limits when ![]() .
.
Consequently, the coefficients ![]() and the expressions giving them
within the open unit disk are continuous from within at the unit circle,
as functions of
and the expressions giving them
within the open unit disk are continuous from within at the unit circle,
as functions of ![]() , and so are the integrals appearing in those
expressions. We may now take the
, and so are the integrals appearing in those
expressions. We may now take the ![]() limit and therefore get the
usual formulas for the Fourier coefficients,
limit and therefore get the
usual formulas for the Fourier coefficients,
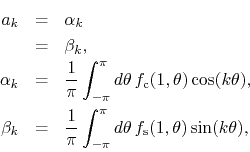
where
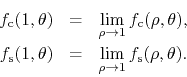
We see therefore that the two trigonometric series of the pair of FC
series we started with, under the very weak hypothesis that they both
converge at one common point, are in fact the DP Fourier series of the DP
functions
![]() and
and
![]() which are
obtained as the
which are
obtained as the ![]() limits of the real part
limits of the real part
![]() and of the imaginary part
and of the imaginary part
![]() of
the inner analytic function
of
the inner analytic function ![]() .
.
It is important to note that ![]() might not be analytic at some points
on the unit circle. Also, so far we cannot state that the Taylor series
might not be analytic at some points
on the unit circle. Also, so far we cannot state that the Taylor series
![]() converges anywhere on the unit circle, besides that single point
at which we assumed the convergence of the pair of FC trigonometric
series. For it to be possible to define the real integrals over the unit
circle, the
converges anywhere on the unit circle, besides that single point
at which we assumed the convergence of the pair of FC trigonometric
series. For it to be possible to define the real integrals over the unit
circle, the ![]() limits of the functions
limits of the functions
![]() and
and
![]() must exist at least almost everywhere on the
unit circle parametrized by
must exist at least almost everywhere on the
unit circle parametrized by ![]() . They may fail to exist at points
where
. They may fail to exist at points
where ![]() has isolated singularities on that circle. Therefore, for the
moment the definition of the trigonometric series as Fourier series on the
unit circle must remain conditioned to the existence of these limits
almost everywhere.
has isolated singularities on that circle. Therefore, for the
moment the definition of the trigonometric series as Fourier series on the
unit circle must remain conditioned to the existence of these limits
almost everywhere.
Note that, if the limits to the unit circle result in isolated
singularities in
![]() or
or
![]() , then
these must be integrable ones along the unit circle, since the
, then
these must be integrable ones along the unit circle, since the ![]() coefficients are all finite.
coefficients are all finite.