Next: The Orthogonality Relations Up: Fourier Theory on the Previous: Fourier Series on the
Let us now show that there is a complete one-to-one correspondence between
arbitrarily given pairs of real FC Fourier series and the inner analytic
functions within the open unit disk. To this end, let us imagine that one
begins the whole argument of the last section over again, but this time
starting with a pair of FC Fourier series. What this means is that there
is a zero-average real function ![]() defined in the periodic
interval such that the coefficients
defined in the periodic
interval such that the coefficients ![]() are given in terms of that
function by the integrals
are given in terms of that
function by the integrals
where we have
![]() , with
, with
![]() even on
even on ![]() and
and
![]() odd on
odd on
![]() . The two Fourier series generated by
. The two Fourier series generated by
![]() and
and
![]() have exactly the same coefficients, and are therefore
the FC series of one another. We may therefore consider the corresponding
functions to be FC functions of one another as well, even if the series do
not converge. We will denote these FC functions by
have exactly the same coefficients, and are therefore
the FC series of one another. We may therefore consider the corresponding
functions to be FC functions of one another as well, even if the series do
not converge. We will denote these FC functions by
![]() in the case of an original cosine series with coefficients
given by
in the case of an original cosine series with coefficients
given by
![]() , and by
, and by
![]() in the case
of an original sine series with coefficients given by
in the case
of an original sine series with coefficients given by
![]() . We have therefore that
. We have therefore that
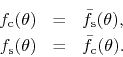
Note that
![]() is in fact odd instead of even, while
is in fact odd instead of even, while
![]() is in fact even instead of odd.
is in fact even instead of odd.
As before, we assume that there is at least one value of ![]() for
which both series in the FC pair converge. We may then use the
coefficients
for
which both series in the FC pair converge. We may then use the
coefficients ![]() to define the inner analytic function
to define the inner analytic function ![]() , as we
did in the previous section, we may identify these coefficients as those
of its Taylor series, and therefore these same coefficients turn out to be
given by
, as we
did in the previous section, we may identify these coefficients as those
of its Taylor series, and therefore these same coefficients turn out to be
given by
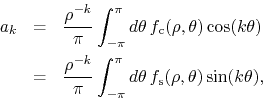
where
![]() and
and
![]() are
respectively the real and imaginary parts of
are
respectively the real and imaginary parts of ![]() . Since the
coefficients
. Since the
coefficients ![]() are in fact independent of
are in fact independent of ![]() in this last set of
expressions, for
in this last set of
expressions, for ![]() , and by construction have the same values as
those given by the previous set of expressions, in
Equation (3), which define them as Fourier coefficients of
, and by construction have the same values as
those given by the previous set of expressions, in
Equation (3), which define them as Fourier coefficients of
![]() , we see that they are continuous from within as functions of
, we see that they are continuous from within as functions of
![]() in the limit
in the limit ![]() , which we may then take.
, which we may then take.
According to the results of the previous section, we conclude therefore
that the two FC Fourier series we started with in this section are in fact
the DP Fourier series of the functions
![]() and
and
![]() in the
in the ![]() limit. Since the coefficients
uniquely identify the function almost everywhere, as discussed in the
introduction, we may now identify these two functions in the
limit. Since the coefficients
uniquely identify the function almost everywhere, as discussed in the
introduction, we may now identify these two functions in the ![]() limit with the two functions
limit with the two functions
![]() and
and
![]() from which the coefficients
from which the coefficients ![]() were obtained in the first place, on
the unit circle. We conclude that the limits
were obtained in the first place, on
the unit circle. We conclude that the limits
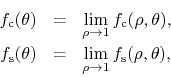
exist and hold almost everywhere over the unit circle. We may consider the
![]() limits of the functions
limits of the functions
![]() and
and
![]() to be the maximally smooth members of sets of functions
that are zero-measure equivalent and lead to the same set of Fourier
coefficients. The functions
to be the maximally smooth members of sets of functions
that are zero-measure equivalent and lead to the same set of Fourier
coefficients. The functions
![]() and
and
![]() , which according to our definitions are the Fourier
Conjugate functions of each other, are also known as Harmonic Conjugate
functions [4], since they are the real and imaginary parts of
an analytic function, and hence are both harmonic functions on the real
plane. They can be obtained from one another by the Hilbert
transform [5]. In the
, which according to our definitions are the Fourier
Conjugate functions of each other, are also known as Harmonic Conjugate
functions [4], since they are the real and imaginary parts of
an analytic function, and hence are both harmonic functions on the real
plane. They can be obtained from one another by the Hilbert
transform [5]. In the ![]() limit we may also get
functions
limit we may also get
functions
![]() and
and
![]() which are
restriction to the unit circle of Harmonic Conjugate functions, if the
function
which are
restriction to the unit circle of Harmonic Conjugate functions, if the
function ![]() is analytic at the limiting point. But in any case they
are Fourier Conjugate to each other.
is analytic at the limiting point. But in any case they
are Fourier Conjugate to each other.
Up to this point we have established that every given pair of FC Fourier
series, obtained from a given pair of FC real functions, such that both
converge together on at least one point on the unit circle, corresponds to
a specific inner analytic function, whose Taylor series converges on at
least that point in the unit circle, and which reproduces the original
pair of FC real function almost everywhere when one takes the ![]() limit from within the open unit disk to the unit circle.
limit from within the open unit disk to the unit circle.
Furthermore, we also see that we may work this argument in reverse. In
other words, given an arbitrary inner analytic function ![]() whose
Taylor series converges on at least one point in the unit circle and which
is well-defined almost everywhere over that circle, we may construct from
it the DP Fourier series of two related functions. These two DP Fourier
series are just the real and imaginary parts of the Taylor series of the
analytic function
whose
Taylor series converges on at least one point in the unit circle and which
is well-defined almost everywhere over that circle, we may construct from
it the DP Fourier series of two related functions. These two DP Fourier
series are just the real and imaginary parts of the Taylor series of the
analytic function ![]() , in the
, in the ![]() limit. Finally, since the
coefficients
limit. Finally, since the
coefficients ![]() are continuous functions of
are continuous functions of ![]() from within at the
unit disk, and since the
from within at the
unit disk, and since the ![]() series converges on at least one point on
the unit circle, we may also conclude that the two corresponding FC
Fourier series converge together on that point of the unit circle.
series converges on at least one point on
the unit circle, we may also conclude that the two corresponding FC
Fourier series converge together on that point of the unit circle.
This completes the establishment of a one-to-one correspondence between,
on the one hand, pairs of real FC Fourier series that converge together on
at least a single point of the periodic interval and, on the other hand,
inner analytic functions that converge on at least one point of the unit
circle and are well-defined almost everywhere over that circle. Note,
however, that the analytic side of this correspondence is the more
powerful one, because given the Fourier coefficients ![]() we may be
able to define a convergent power series
we may be
able to define a convergent power series ![]() and thus an inner
analytic function
and thus an inner
analytic function ![]() even if the corresponding Fourier series diverge
everywhere on the periodic interval.
even if the corresponding Fourier series diverge
everywhere on the periodic interval.
This correspondence can be a useful tool, as it may make it easier to
determine the convergence or lack thereof of given Fourier series. It may
also be used to recover from the coefficients ![]() the function which
generates a given Fourier series, even if that series is divergent. The
way to do this is simply to determine the corresponding inner analytic
function and then calculate the
the function which
generates a given Fourier series, even if that series is divergent. The
way to do this is simply to determine the corresponding inner analytic
function and then calculate the ![]() limit of the real and
imaginary parts of that function. In Appendix C we will
give a few simple examples of this type of procedure.
limit of the real and
imaginary parts of that function. In Appendix C we will
give a few simple examples of this type of procedure.