Next: A Singular Cosine Series Up: Appendix: Examples of Limits Previous: A Regular Sine Series
Consider the Fourier series of the unit-amplitude triangular wave. As is well known it is given by the cosine series
![\begin{displaymath}
S_{\rm c}
=
-\,
\frac{8}{\pi^{2}}
\sum_{j=0}^{\infty}
\frac{1}{(2j+1)^{2}}\,
\cos[(2j+1)\theta].
\end{displaymath}](img341.png)
The corresponding FC series is then
![\begin{displaymath}
\bar{S}_{\rm c}
=
-\,
\frac{8}{\pi^{2}}
\sum_{j=0}^{\infty}
\frac{1}{(2j+1)^{2}}\,
\sin[(2j+1)\theta],
\end{displaymath}](img342.png)
the complex ![]() series is given by
series is given by
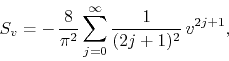
and the complex power series ![]() is given by
is given by
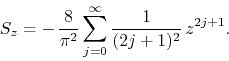
The ratio test tells us that the disk of convergence of ![]() is the
unit disk. If we consider the inner analytic function
is the
unit disk. If we consider the inner analytic function ![]() within this
disk we observe that
within this
disk we observe that ![]() , as expected. We have for the function and
its derivative
, as expected. We have for the function and
its derivative
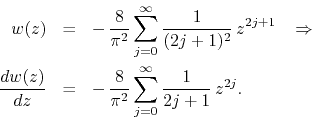
Observe that we have for the derivative the particular value
We may now multiply by ![]() and differentiate again, to obtain
and differentiate again, to obtain
![\begin{eqnarray*}
\frac{d}{dz}
\left[
z\,
\frac{dw(z)}{dz}
\right]
& = &
...
...\\
& = &
-\,
\frac{8}{\pi^{2}}
\sum_{j=0}^{\infty}
z^{2j}.
\end{eqnarray*}](img347.png)
This is a geometrical series and therefore we may write this expression in closed form,
![\begin{eqnarray*}
\frac{d}{dz}
\left[
z\,
\frac{dw(z)}{dz}
\right]
& = &
...
...8}{\pi^{2}}\,
\left(
\frac{1}{1+z}
+
\frac{1}{1-z}
\right).
\end{eqnarray*}](img348.png)
It is now very simple to integrate in order to obtain the derivative of
![]() in closed form, remembering that we should have for it the value
in closed form, remembering that we should have for it the value
![]() at
at ![]() ,
,
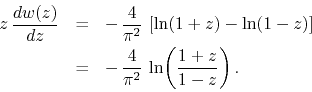
This is the logarithmic derivative of ![]() , which is another inner
analytic function, and it should be noted that it is proportional to the
analytic function
, which is another inner
analytic function, and it should be noted that it is proportional to the
analytic function ![]() for the case of the standard square
wave,
for the case of the standard square
wave,
We get for the derivative of ![]()
This function has two borderline hard singularities at the points where
the triangular wave is not differentiable. Presumably ![]() has two
borderline soft singularities at these points. It seems that the second
integration cannot be done explicitly because the indefinite integral of
the function above cannot be expressed as a finite combination of
elementary functions. We are thus unable to write
has two
borderline soft singularities at these points. It seems that the second
integration cannot be done explicitly because the indefinite integral of
the function above cannot be expressed as a finite combination of
elementary functions. We are thus unable to write ![]() in closed form.
However, we may still obtain partial confirmation of our results by using
the closed form for the derivative of
in closed form.
However, we may still obtain partial confirmation of our results by using
the closed form for the derivative of ![]() . If we differentiate the
Fourier series of the triangular wave with respect to
. If we differentiate the
Fourier series of the triangular wave with respect to ![]() we get
we get
![\begin{displaymath}
\frac{dS_{\rm c}}{d\theta}
=
\frac{8}{\pi^{2}}
\sum_{j=0}^{\infty}
\frac{1}{2j+1}\,
\sin[(2j+1)\theta].
\end{displaymath}](img354.png)
This is equal to ![]() times the Fourier series for the standard square
wave, given in Subsection C.2. On the other hand, if we
use
times the Fourier series for the standard square
wave, given in Subsection C.2. On the other hand, if we
use
![]() and consider the complex derivative of
and consider the complex derivative of ![]() taken in the direction of
taken in the direction of ![]() , we have
, we have
We have therefore
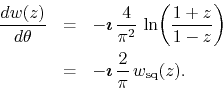
The factor of
![]() simply implements the necessary exchanges of real and
imaginary parts, to account for the exchange of sines and cosines in the
process of differentiation, and the factor of
simply implements the necessary exchanges of real and
imaginary parts, to account for the exchange of sines and cosines in the
process of differentiation, and the factor of ![]() corrects the
normalization. We see therefore that at least the derivative of the
Fourier series at the unit circle is represented correctly by the inner
analytic function
corrects the
normalization. We see therefore that at least the derivative of the
Fourier series at the unit circle is represented correctly by the inner
analytic function ![]() .
.