A Regular Sine Series with Odd $k$

Consider the Fourier series of the standard unit-amplitude square wave. As is well known it is given by the sine series

$$S_{\rm s} = \frac{4}{\pi} \sum_{j=0}^{\infty} \frac{1}{2j+1}\, \sin[(2j+1)\theta].$$

The corresponding FC series is then

$$\bar{S}_{\rm s} = \frac{4}{\pi} \sum_{j=0}^{\infty} \frac{1}{2j+1}\, \cos[(2j+1)\theta],$$

the complex $S_{v}$ series is given by

$$S_{v} = \frac{4}{\pi} \sum_{j=0}^{\infty} \frac{1}{2j+1}\, v^{2j+1},$$

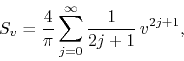
and the complex power series $S_{z}$ is given by

$$S_{z} = \frac{4}{\pi} \sum_{j=0}^{\infty} \frac{1}{2j+1}\, z^{2j+1}.$$

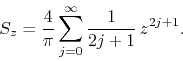
The ratio test tells us that the disk of convergence of $S_{z}$ is the unit disk. If we consider the inner analytic function $w(z)$ within this disk we observe that $w(0)=0$, as expected. We have for the function and its derivative

$$\begin{eqnarray*} w(z) & = & \frac{4}{\pi} \sum_{j=0}^{\infty} \frac{1}{2j+... ...c{dw(z)}{dz} & = & \frac{4}{\pi} \sum_{j=0}^{\infty} z^{2j}. \end{eqnarray*}$$

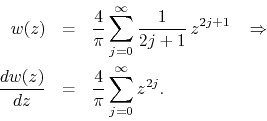
This is a geometrical series and therefore we may write the derivative in closed form,

$$\begin{eqnarray*} \frac{dw(z)}{dz} & = & \frac{4}{\pi}\, \frac{1}{1-z^{2}} ... ...rac{2}{\pi}\, \left( \frac{1}{1+z} + \frac{1}{1-z} \right). \end{eqnarray*}$$

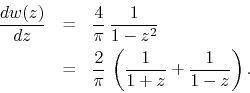
This function has two simple poles at the points where the square wave is discontinuous. These are hard singularities of degree $1$. It is now very simple to integrate in order to obtain the inner analytic function $w(z)$ in closed form, remembering that we should have $w(0)=0$,

$$\begin{eqnarray*} w(z) & = & \frac{2}{\pi}\, \left[ \ln(1+z) - \ln(1-z) ... ... \\ & = & \frac{2}{\pi}\, \ln\!\left(\frac{1+z}{1-z}\right). \end{eqnarray*}$$

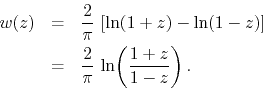
This function has logarithmic singularities at the points where the square wave is discontinuous. These are borderline hard singularities. If we now rationalize the argument of the logarithm in order to write it in the form

$$\frac{1+z}{1-z} = R\,{\rm e}^{\mbox{\boldmath$\imath$}\alpha},$$

then the logarithm is given by

$$\ln\!\left(\frac{1+z}{1-z}\right) = \ln(R)+\mbox{\boldmath$\imath$}\alpha,$$

which allows us to identify the real and imaginary parts of $w(z)$. We may write for the argument

$$\begin{eqnarray*} R\,{\rm e}^{\mbox{\boldmath$\imath$}\alpha} & = & \frac{(1+... ...2\rho\sin(\theta)} {\left(1+\rho^{2}\right)-2\rho\cos(\theta)}. \end{eqnarray*}$$

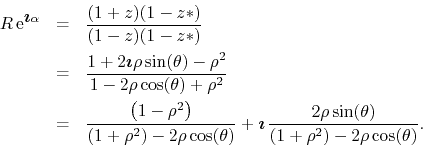
From this it follows, after some algebra, that we have

$$\begin{eqnarray*} R(\rho,\theta) & = & \sqrt { \frac {\left(1+\rho^{2}\rig... ...= & \arctan\!\left[\frac{2\rho\sin(\theta)}{1-\rho^{2}}\right]. \end{eqnarray*}$$

The part which is of interest now is the imaginary one, which is related to the series $S_{\rm s}$,

$$\Im[w(z)] = \frac{2}{\pi}\, \arctan\!\left[\frac{2\rho\sin(\theta)}{1-\rho^{2}}\right].$$

The $\rho\to 1$ limit of this quantity is the function $f_{\rm s}(\theta)$. If we consider the cases $\theta=0$ and $\theta=\pm\pi$, we immediately get zero, because the argument of the arc tangent is zero, and therefore we get $\alpha=0$. Therefore we have

$$\begin{eqnarray*} f_{\rm s}(0) & = & \lim_{\rho\to 1} \Im[w(\rho,0)] \\ &... ...i) & = & \lim_{\rho\to 1} \Im[w(\rho,\pm\pi)] \\ & = & 0. \end{eqnarray*}$$

These are the correct values for the Fourier-series representation of the square wave at these points. For $\theta\neq 0$ and $\theta\neq\pm\pi$ we get

$$\begin{eqnarray*} f_{\rm s}(\theta) & = & \lim_{\rho\to 1} \Im[w(z)] \\ &... ...o\to 1} \arctan\!\left[\frac{2\sin(\theta)}{1-\rho^{2}}\right]. \end{eqnarray*}$$

If $\theta>0$ the argument of the arc tangent goes to positive infinity in the limit, and therefore the arc tangent $\alpha$ approaches $\pi/2$. If $\theta>0$ the argument goes to negative infinity, and therefore $\alpha$ approaches $-\pi/2$. We get therefore the values

$$% \renewedcommand{arraystretch}{2.0} \begin{array}{rclcc... ...s}(\theta) & = & -1 & \mbox{for} & \theta<0, \end{array}$$

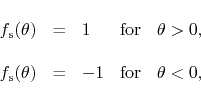
which completes the correct set of values for the standard square wave. The FC function is related to the real part

$$\Re[w(z)] = \frac{1}{\pi}\, \ln\! \left[ \frac {\left... ...theta)} {\left(1+\rho^{2}\right)-2\rho\cos(\theta)} \right].$$

In the $\rho\to 1$ limit this function is singular at $\theta=0$ and $\theta=\pm\pi$. Away from these logarithmic singularities we may write

$$\begin{eqnarray*} \bar{f}_{\rm s}(\theta) & = & \lim_{\rho\to 1} \Re[w(z)] ... ...\pi}\, \ln\!\left[\frac{1+\cos(\theta)}{1-\cos(\theta)}\right]. \end{eqnarray*}$$

We see therefore that the FC function to the square wave is a function with logarithmic singularities at the two points where the original function is discontinuous. The derivative of this conjugate function is easily calculated, and turns out to be

$$\frac{d\bar{f}_{\rm s}(\theta)}{d\theta} = -\, \frac{2}{\pi}\, \frac{1}{\sin(\theta)}.$$

This is a quite a simple function, with two simple poles at $\theta=0$ and $\theta=\pm\pi$. Note that the logarithmic singularities of the FC function $\bar{f}_{\rm s}(\theta)$ are integrable ones, as one would expect since the Fourier coefficients are finite.

Note that we get a free set of integration formulas out of this effort. Since the coefficients $a_{k}$ can be written as integrals involving $\bar{f}_{\rm s}(\theta)$, we have at once that for odd $k=2j+1$

$$\int_{-\pi}^{\pi}d\theta\, \ln\!\left[\frac{1+\cos(\theta)}{1-\cos(\theta)}\right] \cos(k\theta) = \frac{4\pi}{k},$$

while for even $k=2j$

$$\int_{-\pi}^{\pi}d\theta\, \ln\!\left[\frac{1+\cos(\theta)}{1-\cos(\theta)}\right] \cos(k\theta) = 0,$$

for $k>0$. Note that $\bar{f}_{\rm s}(\theta)$ is an even function of $\theta$, so that these integrals are not zero by parity arguments, and therefore we also have

$$\int_{0}^{\pi}d\theta\, \ln\!\left[\frac{1+\cos(\theta)}{1-\cos(\theta)}\right] \cos(k\theta) = 0,$$

for $k>0$.