Next: Bibliography Up: Appendix: Examples of Limits Previous: A Regular Cosine Series
Consider the Fourier series of the Dirac delta ``function'' centered at
![]() , which we denote by
, which we denote by
![]() . We
may easily calculate its Fourier coefficients using the rules of
manipulation of
. We
may easily calculate its Fourier coefficients using the rules of
manipulation of
![]() , thus obtaining
, thus obtaining
![]() and
and
![]() for all
for all ![]() . The series is therefore the complete Fourier series given by
. The series is therefore the complete Fourier series given by
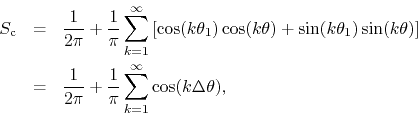
where
![]() . Apart from the constant term this
is in fact a cosine series on this new variable. Clearly, this series
diverges at all points in the interval
. Apart from the constant term this
is in fact a cosine series on this new variable. Clearly, this series
diverges at all points in the interval ![]() . Undaunted by this, we
construct the FC series, with respect to the new variable
. Undaunted by this, we
construct the FC series, with respect to the new variable ![]() ,
,
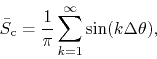
a series that is also divergent, this time almost everywhere. If we define
![]() and
and
![]() the corresponding
complex series
the corresponding
complex series ![]() is then given by
is then given by
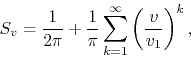
where we included the ![]() term, and the corresponding complex power
series
term, and the corresponding complex power
series ![]() is given by
is given by
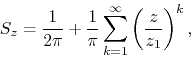
where ![]() and
and ![]() is a point on the unit circle. This is
a geometrical series that converges everywhere strictly inside the unit
disk, where it therefore converges to the analytic function
is a point on the unit circle. This is
a geometrical series that converges everywhere strictly inside the unit
disk, where it therefore converges to the analytic function
This function has a simple pole at the singular point of the Dirac delta
``function''. This is a hard singularity of degree ![]() . As was discussed
in Section 6, strictly speaking this is not an inner
analytic function by the definition which we adopted here, for two
reasons. First,
. As was discussed
in Section 6, strictly speaking this is not an inner
analytic function by the definition which we adopted here, for two
reasons. First, ![]() is not zero, which is easily fixed by just
taking off the constant term. Second, it does not reduce to a real
function over the real axis. However, as was shown in
Section 6, it does reduce to a real function over the
straight line
is not zero, which is easily fixed by just
taking off the constant term. Second, it does not reduce to a real
function over the real axis. However, as was shown in
Section 6, it does reduce to a real function over the
straight line ![]() , with real
, with real ![]() , since in this case we have
, since in this case we have
which is a real function of the real variable ![]() . Since we have
. Since we have
![]() , we see that this is an inner analytic
function rotated by an angle
, we see that this is an inner analytic
function rotated by an angle ![]() around the origin. We see
therefore that our definition of inner analytic function can be easily
generalized in this way, to make reference to any straight line going
through the origin. We also see that there is nothing to prevent us from
treating this function just like any other inner analytic function.
around the origin. We see
therefore that our definition of inner analytic function can be easily
generalized in this way, to make reference to any straight line going
through the origin. We also see that there is nothing to prevent us from
treating this function just like any other inner analytic function.
We now examine the real part of the function ![]() , which was
derived in Section 6, and which is related to the series
, which was
derived in Section 6, and which is related to the series
![]() ,
,
The ![]() limit of
limit of
![]() gives us back the constant
term and the original cosine series
gives us back the constant
term and the original cosine series ![]() , and in fact attributes
well-defined finite values to it almost everywhere, even though the
original series is divergent. As was shown directly in
Section 6, in the
, and in fact attributes
well-defined finite values to it almost everywhere, even though the
original series is divergent. As was shown directly in
Section 6, in the ![]() limit this real part has all
the required properties of the Dirac delta ``function'', including the
fact that it assumes the value zero almost everywhere. Note that although
the singularity of
limit this real part has all
the required properties of the Dirac delta ``function'', including the
fact that it assumes the value zero almost everywhere. Note that although
the singularity of ![]() at
at ![]() is a simple pole and thus
not an integrable one, the real part of
is a simple pole and thus
not an integrable one, the real part of ![]() is integrable if
one crosses the singularity in a specific direction, which in this case is
the direction of the integration along the unit circle.
is integrable if
one crosses the singularity in a specific direction, which in this case is
the direction of the integration along the unit circle.
It is interesting that we may also write a closed expression for the real
function which is the FC function of the Dirac delta ``function''. We just
consider the imaginary part of ![]() , which is related to the
series
, which is related to the
series
![]() ,
,
We now take the ![]() limit, assuming that
limit, assuming that
![]() , and
since this is an actual function we may write
, and
since this is an actual function we may write
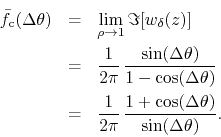
This is just a regular function except for a simple pole at
![]() , and in fact quite a simple rational function involving
trigonometric functions.
, and in fact quite a simple rational function involving
trigonometric functions.
Note that we get a free set of integration formulas out of this effort.
Since the coefficients ![]() can be written as integrals involving
can be written as integrals involving
![]() , we have at once that for all
, we have at once that for all ![]()
We may easily construct from this single Dirac delta ``function'' a pair
of such ``functions'' which relates to the derivative of the standard
square wave. All we have to do is to use the values ![]() and
and
![]() and add to the delta ``function'' at zero given by
and add to the delta ``function'' at zero given by
![]() the delta ``function'' at
the delta ``function'' at ![]() given by
given by
![]() . If we call the corresponding analytic functions
. If we call the corresponding analytic functions
![]() and
and ![]() , we have for the function
, we have for the function
![]() corresponding to the pair
corresponding to the pair
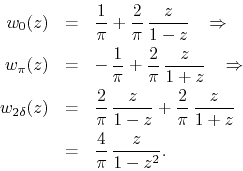
This is an inner analytic function with two simple poles, one at ![]() and
one at
and
one at ![]() . If, on the other hand, we consider the logarithmic
derivative of the analytic function
. If, on the other hand, we consider the logarithmic
derivative of the analytic function ![]() of the standard square
wave, we get
of the standard square
wave, we get
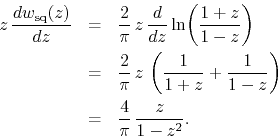
We see therefore that we do indeed have
In terms of derivatives with respect to ![]() this is written as
this is written as
where once again the factor of
![]() has the role of exchanging real and
imaginary parts, and thus sines and cosines.
has the role of exchanging real and
imaginary parts, and thus sines and cosines.
Observe that this is an example in which, although the function
![]() is analytic on the open unit disk, the series
is analytic on the open unit disk, the series ![]() is
not convergent on any points of the unit circle, and hence the two FC
Fourier series do not converge together on any points of the unit circle.
It is therefore outside the hypotheses we used in most of this paper, but
it is still full of meaning. This indicates that there is more in this
structure than has been analyzed so far. If fact, it is quite possible
that the whole structure of distributions such as the one related to the
Dirac delta ``function'' is lurking on the rim of the maximum disk of
convergence of the series
is
not convergent on any points of the unit circle, and hence the two FC
Fourier series do not converge together on any points of the unit circle.
It is therefore outside the hypotheses we used in most of this paper, but
it is still full of meaning. This indicates that there is more in this
structure than has been analyzed so far. If fact, it is quite possible
that the whole structure of distributions such as the one related to the
Dirac delta ``function'' is lurking on the rim of the maximum disk of
convergence of the series ![]() of the inner analytic functions
of the inner analytic functions
![]() corresponding to divergent trigonometric series, that is,
on the rim of the unit disk.
corresponding to divergent trigonometric series, that is,
on the rim of the unit disk.