Next: Remainders of Fourier Series Up: Complex Analysis of Real Previous: Action on the Fourier
In order to obtain a certain infinite collection of identities satisfied by all zero-average integrable real functions and their Fourier-conjugate real functions, which will be very important later, we start by examining the action of the compact Hilbert transform on the products of arbitrarily given integrable real functions and the elements of the Fourier basis. We will prove the following theorem.
where
![]() and
and
![]() .
.
In order to prove this theorem we start from the expression in
Equation (17), exchanging ![]() for the product
for the product
![]() , which is also an inner analytic function so long as
, which is also an inner analytic function so long as ![]() is an arbitrary positive integer power, which it is since we assume that
is an arbitrary positive integer power, which it is since we assume that
![]() . We therefore have
. We therefore have
| (44) |
where both ![]() and
and ![]() are on the circle
are on the circle ![]() of radius
of radius ![]() within the open unit disk. We may now write all quantities in this
equation in terms of
within the open unit disk. We may now write all quantities in this
equation in terms of ![]() ,
, ![]() and
and ![]() ,
,
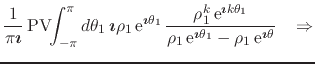 |
|||
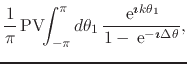 |
(45) |
where
![]() and
and
![]() .
Note that, since by construction the real and imaginary parts
.
Note that, since by construction the real and imaginary parts
![]() and
and
![]() of
of
![]() for
for
![]() are integrable real functions on the unit circle, and since
there are no other dependencies on
are integrable real functions on the unit circle, and since
there are no other dependencies on ![]() in this equation, we may now
take the
in this equation, we may now
take the
![]() limit of this expression, in which the
principal value acquires its usual real meaning on the unit circle, thus
obtaining
limit of this expression, in which the
principal value acquires its usual real meaning on the unit circle, thus
obtaining
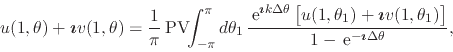 |
(46) |
where
![]() and
and
![]() .
Once more, in order to identify separately the real and imaginary parts of
this equation, we must now rationalize the integrand. Using this time the
form shown in Equation (22) for the factor to be
rationalized, we get
.
Once more, in order to identify separately the real and imaginary parts of
this equation, we must now rationalize the integrand. Using this time the
form shown in Equation (22) for the factor to be
rationalized, we get
where
![]() and
and ![]() , with
, with
![]() . Expanding the numerator in the integrand of
this integral we have
. Expanding the numerator in the integrand of
this integral we have
| (48) | |||
and therefore we are left with
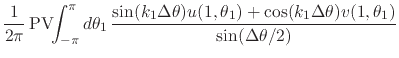 |
|||
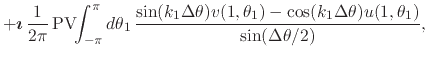 |
(49) | ||
where
![]() and
and ![]() , with
, with
![]() . Separating the real and imaginary parts we
therefore obtain an infinite collection of identities in the form
. Separating the real and imaginary parts we
therefore obtain an infinite collection of identities in the form
where
![]() and
and
![]() .
Recalling now that
.
Recalling now that
![]() , and also that
, and also that
![]() , almost everywhere over the unit circle, one
obtains the results in Equation (43), and therefore this
completes the proof of Theorem 4.
, almost everywhere over the unit circle, one
obtains the results in Equation (43), and therefore this
completes the proof of Theorem 4.
Note that since this is an infinite collection of integral identities,
satisfied by ![]() and
and ![]() for all strictly positive
for all strictly positive ![]() , it
follows that the right-hand sides of the equations above do not, in fact,
depend on
, it
follows that the right-hand sides of the equations above do not, in fact,
depend on ![]() . If one recognizes in the first term of each one of these
two equations the well-known result for the
. If one recognizes in the first term of each one of these
two equations the well-known result for the ![]() partial sums of
the corresponding Fourier series in terms of Dirichlet
integrals [#!FSchurchill!#], then it follows that the other terms must be
the corresponding remainders. This provides us with some level of
understanding of the nature of this infinite set of identities. In the
next section we will prove that one does obtain in fact the partial sums
and remainders of the corresponding Fourier series directly from our
complex-analytic structure.
partial sums of
the corresponding Fourier series in terms of Dirichlet
integrals [#!FSchurchill!#], then it follows that the other terms must be
the corresponding remainders. This provides us with some level of
understanding of the nature of this infinite set of identities. In the
next section we will prove that one does obtain in fact the partial sums
and remainders of the corresponding Fourier series directly from our
complex-analytic structure.