Next: Notes on the Convergence Up: Complex Analysis of Real Previous: Orthogonality Relations
Let us now prove the completeness of the Fourier basis. In this context the concept of completeness is that of a basis within a vector space. We will first give a simple and direct proof of completeness, which is however subject to a slight limitation regarding the vector space for which the basis is shown to be complete, using the analytic structure within the open unit disk, and later establish the relation of the concept of completeness with the so-called completeness relation. The proof of completeness using the completeness relation is not subject to any such limitation.
In this section we will prove the following completeness theorem.
The proof consists of establishing that, given an arbitrary integrable
real function ![]() on the unit circle, which is orthogonal to
all the elements of the Fourier basis, according to the scalar product
defined in Equation (25), it then follows that
on the unit circle, which is orthogonal to
all the elements of the Fourier basis, according to the scalar product
defined in Equation (25), it then follows that
![]() must be zero almost everywhere. Note that the orthogonality
to the elements of the basis means that
must be zero almost everywhere. Note that the orthogonality
to the elements of the basis means that ![]() is such that all
its Fourier coefficients, as defined in Equation (4), are
zero.
is such that all
its Fourier coefficients, as defined in Equation (4), are
zero.
Let ![]() be a real function on the unit circle which can be
obtained as the
be a real function on the unit circle which can be
obtained as the
![]() limit of an inner analytic function. We
assume that it is orthogonal to all the elements of the basis, so that all
its Fourier coefficients are zero, that is, we assume that for this
function we have
limit of an inner analytic function. We
assume that it is orthogonal to all the elements of the basis, so that all
its Fourier coefficients are zero, that is, we assume that for this
function we have ![]() ,
, ![]() and
and ![]() , for all
, for all
![]() . Since we thus have all the Fourier
coefficients of
. Since we thus have all the Fourier
coefficients of ![]() , we may use the construction presented
in [#!CAoRFI!#] in order to determine the corresponding inner analytic
function. However, since all the Fourier coefficients are zero, it follows
at once from the step of that construction given in
Equation (5) that for
, we may use the construction presented
in [#!CAoRFI!#] in order to determine the corresponding inner analytic
function. However, since all the Fourier coefficients are zero, it follows
at once from the step of that construction given in
Equation (5) that for ![]() the complex coefficients
the complex coefficients
![]() are zero for all
are zero for all ![]() . Therefore, the power series
. Therefore, the power series ![]() constructed in the next step of the process, given in
Equation (6), is identically zero and thus converges
trivially to the identically zero complex function
constructed in the next step of the process, given in
Equation (6), is identically zero and thus converges
trivially to the identically zero complex function
![]() on the whole complex plane.
on the whole complex plane.
The analyticity region of ![]() includes the unit circle, and
therefore the series converges to zero there. Since on the one hand the
series converges to zero, and on the other hand we know that for
includes the unit circle, and
therefore the series converges to zero there. Since on the one hand the
series converges to zero, and on the other hand we know that for ![]() it necessarily converges to the restriction of
it necessarily converges to the restriction of ![]() to the unit
circle, it follows that the restriction, including both real and imaginary
parts, must be zero everywhere on the unit circle. Therefore it follows
that
to the unit
circle, it follows that the restriction, including both real and imaginary
parts, must be zero everywhere on the unit circle. Therefore it follows
that ![]() and the identically zero real function coincide
everywhere on the unit circle, and therefore we conclude that
and the identically zero real function coincide
everywhere on the unit circle, and therefore we conclude that
![]() everywhere on that circle. This establishes that the
Fourier basis is complete for the space of all integrable real functions
defined on the periodic interval, which can be obtained as the
everywhere on that circle. This establishes that the
Fourier basis is complete for the space of all integrable real functions
defined on the periodic interval, which can be obtained as the
![]() limits of inner analytic functions. This completes the first
version of the proof of Theorem 1, which is valid for the
vector space of real functions just described.
limits of inner analytic functions. This completes the first
version of the proof of Theorem 1, which is valid for the
vector space of real functions just described.
Note that, since all possible inner analytic functions are given by
convergent power series within the open unit disk, and since these power
series can be understood as expansions of those inner analytic functions
in the Taylor basis of functions given by the non-negative powers
![]() , we
may say that this Taylor basis is complete for the space of all inner
analytic functions. Since the proof of the completeness of the Fourier
basis given above was obtained from the complex-analytic structure within
the open unit disk, it becomes clear that the completeness of the Fourier
basis on the unit circle is a consequence of the completeness of the
Taylor basis within the open unit disk. This adds to the relationship
between the Fourier basis on the unit circle and the Taylor basis on the
unit disk, which was first established during the discussion involving the
orthogonality of the Fourier basis, in Section 3. In addition to
all this, within the spaces generated by either basis one may define
scalar products that induce positive-definite norms, thus making them both
Hilbert spaces, as is discussed in Appendix A.
, we
may say that this Taylor basis is complete for the space of all inner
analytic functions. Since the proof of the completeness of the Fourier
basis given above was obtained from the complex-analytic structure within
the open unit disk, it becomes clear that the completeness of the Fourier
basis on the unit circle is a consequence of the completeness of the
Taylor basis within the open unit disk. This adds to the relationship
between the Fourier basis on the unit circle and the Taylor basis on the
unit disk, which was first established during the discussion involving the
orthogonality of the Fourier basis, in Section 3. In addition to
all this, within the spaces generated by either basis one may define
scalar products that induce positive-definite norms, thus making them both
Hilbert spaces, as is discussed in Appendix A.
Let us now turn to the usual completeness relation. Let us first write it
down and then exhibit its usefulness. The relation can be understood as
the expression, as a Fourier series, of the Dirac delta ``function''
defined with respect to a point given by the angle ![]() on the
unit circle, which we examined in great detail in [#!CAoRFII!#], and
which we denote by
on the
unit circle, which we examined in great detail in [#!CAoRFII!#], and
which we denote by
![]() . As we have shown
in [#!CAoRFII!#], using the usual rules for the manipulation of the delta
``function'', one finds that the corresponding Fourier coefficients are
given by
. As we have shown
in [#!CAoRFII!#], using the usual rules for the manipulation of the delta
``function'', one finds that the corresponding Fourier coefficients are
given by
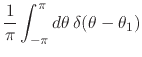 |
|||
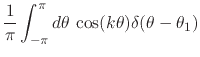 |
|||
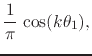 |
|||
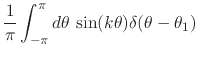 |
|||
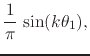 |
(26) |
for
![]() , so that the completeness relation is
given by the Fourier expansion, that turns out to be a bi-linear form on
the elements of the Fourier basis,
, so that the completeness relation is
given by the Fourier expansion, that turns out to be a bi-linear form on
the elements of the Fourier basis,
which is manifestly divergent, but which can be made to converge for all
values of ![]() , so that we may recover the delta ``function'' almost
everywhere, in fact everywhere but at
, so that we may recover the delta ``function'' almost
everywhere, in fact everywhere but at ![]() , through the use of the
summation rule given in Equation (12),
, through the use of the
summation rule given in Equation (12),
This is equivalent to the definition of the delta ``function'' as the
![]() limit of the real part of the inner analytic function
given by
limit of the real part of the inner analytic function
given by
| (29) |
as was discussed in detail in [#!CAoRFII!#]. One can use the expansion in Equation (27), possibly regulated as in Equation (28), to prove the completeness of the basis, while operating strictly in terms of real objects on or near the unit circle. Here is how this can be done.
If we assume that an arbitrary integrable real function ![]() on
the unit circle is given, which is such that its scalar products with all
the elements of the basis are zero, then we have the infinite set of
equations
on
the unit circle is given, which is such that its scalar products with all
the elements of the basis are zero, then we have the infinite set of
equations
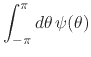 |
|||
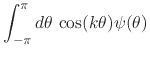 |
|||
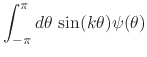 |
(30) |
for all
![]() . We may therefore construct an
infinite linear combination of all these equations, with the coefficients
carefully chosen as shown below, involving an arbitrary parameter
. We may therefore construct an
infinite linear combination of all these equations, with the coefficients
carefully chosen as shown below, involving an arbitrary parameter
![]() in the interval
in the interval ![]() and an auxiliary strictly
positive real variable
and an auxiliary strictly
positive real variable ![]() , where the right-hand side is still zero,
, where the right-hand side is still zero,
![\begin{eqnarray*}
\left[
\frac{1}{2\pi}
\right]
\int_{-\pi}^{\pi}d\theta\,
...
...(k\theta)\psi(\theta)
\hspace{1em}
& = &
0
\;\;\;\Rightarrow
\end{eqnarray*}](img126.png)
![\begin{displaymath}
\int_{-\pi}^{\pi}d\theta\,
\left\{
\frac{1}{2\pi}
+
\fr...
... \sin(k\theta)
\right]
\right\}
\psi(\theta)
\;\;=\;\;
0.
\end{displaymath}](img127.png) |
(31) |
Since the expression within curly brackets in this last integral is now
seen to be the regulated expansion of
![]() in the
Fourier basis, shown in Equation (28), we may therefore
take the
in the
Fourier basis, shown in Equation (28), we may therefore
take the
![]() limit and write that
limit and write that
| (32) |
Finally, using the rules of manipulation of the delta ``function'', when
and where ![]() is continuous, which it therefore must be almost
everywhere, we have
is continuous, which it therefore must be almost
everywhere, we have
| (33) |
Since ![]() is an arbitrary value of
is an arbitrary value of ![]() , we conclude that
, we conclude that
![]() is zero everywhere. This completes the second version of
the proof of Theorem 1, which is valid for the vector space of
all integrable real functions defined on the unit circle, regardless of
whether or not they can be obtained from an inner analytic function.
is zero everywhere. This completes the second version of
the proof of Theorem 1, which is valid for the vector space of
all integrable real functions defined on the unit circle, regardless of
whether or not they can be obtained from an inner analytic function.
Note that, in a sense, this method of proof of the completeness of the
Fourier basis is a little more limited than the direct proof using the
analytic structure within the open unit disk, because we must assume
during the argument that ![]() is continuous almost everywhere.
However, since this hypothesis does get confirmed a posteriori by the
result obtained, this is not a true limitation.
is continuous almost everywhere.
However, since this hypothesis does get confirmed a posteriori by the
result obtained, this is not a true limitation.
On the other hand, this second proof is less limited than the first
one because in this case the vector space of functions for which one shows
that the basis is complete is the space of integrable real functions
without removable singularities defined on the interval ![]() , with
no reference to whether or not these functions can be obtained as
the
, with
no reference to whether or not these functions can be obtained as
the
![]() limits of inner analytic functions.
limits of inner analytic functions.
In fact, by establishing the completeness of the Fourier basis without any
recourse to the
![]() limit for the real functions, as a
corollary of this second proof we have shown that there is no integrable
real function on the unit circle, other that the identically zero real
function, which corresponds to the identically zero inner analytic
function. As a consequence of this, there is no integrable real function
defined on the unit circle that cannot be represented by an unique inner
analytic function.
limit for the real functions, as a
corollary of this second proof we have shown that there is no integrable
real function on the unit circle, other that the identically zero real
function, which corresponds to the identically zero inner analytic
function. As a consequence of this, there is no integrable real function
defined on the unit circle that cannot be represented by an unique inner
analytic function.