Next: Bibliography Up: Complex Analysis of Real Previous: Acknowledgments
Given two inner analytic functions ![]() and
and ![]() , we consider
the complex contour integral over the circle
, we consider
the complex contour integral over the circle ![]() of radius
of radius ![]() ,
with
,
with ![]() , given by
, given by
| (61) |
Since the integrand in this expression is not analytic, the integral
depends on the circuit, and therefore on ![]() . Therefore, what we
have here is in fact a one-parameter family of integrals. We will show
that for each value of
. Therefore, what we
have here is in fact a one-parameter family of integrals. We will show
that for each value of ![]() this integral defines a scalar product
within the space of inner analytic functions, which induces in that space
a positive-definite norm. If we write the integral in terms of the
integration variable
this integral defines a scalar product
within the space of inner analytic functions, which induces in that space
a positive-definite norm. If we write the integral in terms of the
integration variable ![]() , with constant
, with constant ![]() , we get for this
scalar product
, we get for this
scalar product
| (62) |
If we now make both ![]() and
and ![]() equal to
equal to
![]() , we get
, we get
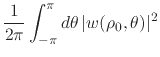 |
|||
![$\displaystyle \frac{1}{2\pi}
\int_{-\pi}^{\pi}d\theta\,
\left[
u^{2}(\rho_{0},\theta)
+
v^{2}(\rho_{0},\theta)
\right]$](img239.png) |
|||
| (63) |
which is a manifestly real and positive quantity, that is zero if and only
if
![]() for all
for all ![]() , which in turn is equivalent to
, which in turn is equivalent to
![]() for all
for all ![]() and all
and all ![]() within the open unit
disk, because all zeros of an analytic function must be isolated, unless
it is the identically zero function. Therefore, for each value of the
parameter
within the open unit
disk, because all zeros of an analytic function must be isolated, unless
it is the identically zero function. Therefore, for each value of the
parameter ![]() the real quantity
the real quantity ![]() is a positive-definite norm
on the space of all inner analytic functions which, as was observed
in [#!CAoRFI!#], forms a vector space over the field of complex numbers.
That vector space is thus seen to constitute a complex Hilbert space, with
this scalar product and the associated positive-definite norm.
is a positive-definite norm
on the space of all inner analytic functions which, as was observed
in [#!CAoRFI!#], forms a vector space over the field of complex numbers.
That vector space is thus seen to constitute a complex Hilbert space, with
this scalar product and the associated positive-definite norm.
We can also see from the equation above that the scalar product and the
norm reduce naturally to the corresponding definitions for the real
functions ![]() and
and ![]() on the unit circle, when we take
the
on the unit circle, when we take
the
![]() limit, thus establishing a close correspondence
between these two identical real Hilbert spaces on the unit circle and the
complex Hilbert space on the unit disk. In addition to this, for any value
of
limit, thus establishing a close correspondence
between these two identical real Hilbert spaces on the unit circle and the
complex Hilbert space on the unit disk. In addition to this, for any value
of ![]() within the open interval
within the open interval ![]() we also have a pair of
identical real Hilbert spaces with the real functions
we also have a pair of
identical real Hilbert spaces with the real functions
![]() and
and
![]() on the circle of radius
on the circle of radius ![]() .
.
We may now show that the Taylor basis of functions around the origin, which is complete to generate the whole space of inner analytic functions, and which consists of the set of non-negative powers
| (64) |
is in fact an orthogonal basis according to this definition of the scalar
product. If we make
![]() and
and
![]() , we get
, we get
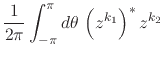 |
|||
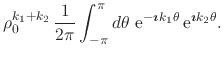 |
(65) |
Using now the first result shown in Equation (18) we obtain the orthogonality relation for the Taylor basis,
| (66) |
Since the integer powers are analytic on the whole complex plane, there is
no obstruction to taking the
![]() limit, and thus we see
that in this case the Taylor basis is not only orthogonal, but also
normalized,
limit, and thus we see
that in this case the Taylor basis is not only orthogonal, but also
normalized,
| (67) |
with ![]() for all
for all ![]() , where the scalar product is now defined on
the unit circle. If we write the inner analytic functions in terms of
their Taylor series around the origin,
, where the scalar product is now defined on
the unit circle. If we write the inner analytic functions in terms of
their Taylor series around the origin,
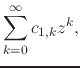 |
|||
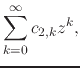 |
(68) |
we obtain for the scalar product, since we may always integrate convergent power series term-by-term,
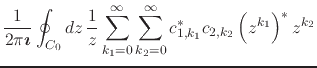 |
|||
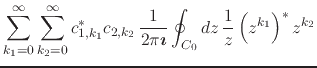 |
|||
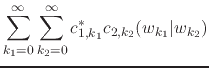 |
|||
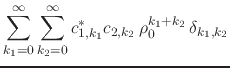 |
|||
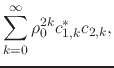 |
(69) |
where we identified the scalar product
![]() and then
used the orthogonality relations of the Taylor basis. So long as
and then
used the orthogonality relations of the Taylor basis. So long as
![]() , and so long as
, and so long as ![]() and
and ![]() are exponentially
bounded, this series converges exponentially fast. We may also write the
corresponding expression for the norm, if we make
are exponentially
bounded, this series converges exponentially fast. We may also write the
corresponding expression for the norm, if we make
![]() and
and
![]() ,
,
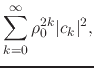 |
(70) |
with the same conditions for the convergence of the series. In all this
structure, if we take the
![]() limit, the scalar product
and the norm may in general diverge, unlike what happens in the case of
the elements of the Taylor basis. However, so long as
limit, the scalar product
and the norm may in general diverge, unlike what happens in the case of
the elements of the Taylor basis. However, so long as ![]() all the
inner analytic functions have finite norms and finite scalar products with
one another. In some cases, it may be possible to determine the values of
these quantities on the unit circle using the
all the
inner analytic functions have finite norms and finite scalar products with
one another. In some cases, it may be possible to determine the values of
these quantities on the unit circle using the
![]() limit,
even if the corresponding series expressions written directly on the unit
circle diverge.
limit,
even if the corresponding series expressions written directly on the unit
circle diverge.
Perhaps the best way to characterize this structure is as a one-parameter
family of pairs of identical real Hilbert spaces, one associated to the
real parts and another associated to the imaginary parts of the inner
analytic functions, where the parameter is the radius ![]() of each
circle within the unit disk, which are connected to each other by a
process of analytic continuation. For each value of
of each
circle within the unit disk, which are connected to each other by a
process of analytic continuation. For each value of ![]() within the
open interval
within the
open interval ![]() there is a one-to-one mapping between the inner
analytic functions on the open unit disk and the real functions obtained
as the real parts of these inner analytic function restricted to the
circle of radius
there is a one-to-one mapping between the inner
analytic functions on the open unit disk and the real functions obtained
as the real parts of these inner analytic function restricted to the
circle of radius ![]() . This one-to-one mapping preserves the scalar
product and the norm, as they are defined within each space. This fact is
still true even in the
. This one-to-one mapping preserves the scalar
product and the norm, as they are defined within each space. This fact is
still true even in the
![]() limit, although in that case
not every real object at the unit circle, resulting from the limit, is a
normal real function, and although in many cases the norms and scalar
products may diverge in the limit.
limit, although in that case
not every real object at the unit circle, resulting from the limit, is a
normal real function, and although in many cases the norms and scalar
products may diverge in the limit.
Note that the integral defining the scalar product of the inner analytic
functions is a one-dimensional integral over the circle of radius
![]() , despite the fact that each complex inner analytic function
consist of a pair of real functions of two variables. However, this is a
natural characteristic of the scalar product in this context, since it is
a well-known fact that an analytic function is completely determined on a
two-dimensional region of the complex plane by its values only at a
one-dimensional boundary of that region. In this way, although only a
one-dimensional restriction of the inner analytic function is explicitly
taken into account in the integral over the circle of radius
, despite the fact that each complex inner analytic function
consist of a pair of real functions of two variables. However, this is a
natural characteristic of the scalar product in this context, since it is
a well-known fact that an analytic function is completely determined on a
two-dimensional region of the complex plane by its values only at a
one-dimensional boundary of that region. In this way, although only a
one-dimensional restriction of the inner analytic function is explicitly
taken into account in the integral over the circle of radius ![]() that defines the scalar product, that restriction still includes
implicitly the whole structure of the inner analytic function within the
corresponding disk of radius
that defines the scalar product, that restriction still includes
implicitly the whole structure of the inner analytic function within the
corresponding disk of radius ![]() . Therefore, it is perhaps arguable
that the most natural definition of the scalar product is that associated
to the choice
. Therefore, it is perhaps arguable
that the most natural definition of the scalar product is that associated
to the choice ![]() , despite the convergence issues that this
choice may involve.
, despite the convergence issues that this
choice may involve.