Next: Completeness Relation Up: Complex Analysis of Real Previous: Fourier Series
The Fourier series of an integrable real function can be understood as the expansion of that real function in the Fourier basis of functions, which consists of the set of functions
Let us now show that this is an orthogonal basis. Of course this can be
done using the standard form of the scalar product between two real
functions on the unit circle, by simply calculating a set of easy
integrals by elementary means. However, what we want to do here is to show
that both the form of the scalar product and the relations of
orthogonality and norm are contained within the structure of the inner
analytic functions, and can be derived from that structure. In fact, we
will show that these elements can be obtained from a particular set of
functions, the powers ![]() , with
, with ![]() , and their multiplicative
inverses
, and their multiplicative
inverses ![]() . We start by noting that, if
. We start by noting that, if ![]() is any circle centered
at the origin, including the unit circle, then from the residues theorem
we have that
is any circle centered
at the origin, including the unit circle, then from the residues theorem
we have that
| (14) |
where ![]() is an arbitrary integer, and where
is an arbitrary integer, and where ![]() is the
Kronecker delta. This is so because the integral can be calculated by
residues, and a function which is a simple power, either positive or
negative, is its own Laurent series, which has only one term. Therefore,
its residue at
is the
Kronecker delta. This is so because the integral can be calculated by
residues, and a function which is a simple power, either positive or
negative, is its own Laurent series, which has only one term. Therefore,
its residue at ![]() is zero unless
is zero unless ![]() , in which case it is equal to
one. Using this result for the case
, in which case it is equal to
one. Using this result for the case ![]() , where the integers
, where the integers ![]() and
and
![]() are in the set
are in the set
![]() , we have
, we have
| (15) |
while using the same expression for ![]() , with the limitation that
, with the limitation that
![]() , which means that
, which means that ![]() and
and ![]() cannot both be zero, we have
cannot both be zero, we have
| (16) |
This is also a consequence of the Cauchy-Goursat theorem, since in this
case the integrand is analytic within the unit disk. Note that the power
![]() with
with ![]() is itself an inner analytic function. Writing these
two relations in terms of the integration variable
is itself an inner analytic function. Writing these
two relations in terms of the integration variable ![]() we have
we have
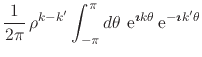 |
|||
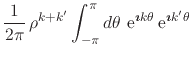 |
(17) |
since
![]() , where in the second equation we must have
, where in the second equation we must have
![]() . So long as
. So long as ![]() the powers of
the powers of ![]() can be eliminated
from the second equation, and since the right-hand term of the first
equation is zero unless
can be eliminated
from the second equation, and since the right-hand term of the first
equation is zero unless ![]() , they can also be eliminated from the first
equation, so that we have
, they can also be eliminated from the first
equation, so that we have
where in the second equation we must have ![]() . Note that this is
valid not only on the unit circle, but for all values of
. Note that this is
valid not only on the unit circle, but for all values of ![]() so long as
so long as
![]() . Expanding the complex exponentials, with the use of the
Euler formula, and collecting real and imaginary parts, we have
. Expanding the complex exponentials, with the use of the
Euler formula, and collecting real and imaginary parts, we have
![$\displaystyle \frac{1}{\pi}
\int_{-\pi}^{\pi}d\theta\,
\left[
\cos(k\theta)\cos(k'\theta)
+
\sin(k\theta)\sin(k'\theta)
\right]
\hspace{2em}$](img83.png) |
|||
![$\displaystyle +
\mbox{\boldmath$\imath$}\,
\frac{1}{\pi}
\int_{-\pi}^{\pi}d\theta\,
\left[
\sin(k\theta)\cos(k'\theta)
-
\cos(k\theta)\sin(k'\theta)
\right]$](img84.png) |
|||
![$\displaystyle \frac{1}{\pi}
\int_{-\pi}^{\pi}d\theta\,
\left[
\cos(k\theta)\cos(k'\theta)
-
\sin(k\theta)\sin(k'\theta)
\right]
\hspace{2em}$](img86.png) |
|||
![$\displaystyle +
\mbox{\boldmath$\imath$}\,
\frac{1}{\pi}
\int_{-\pi}^{\pi}d\theta\,
\left[
\sin(k\theta)\cos(k'\theta)
+
\cos(k\theta)\sin(k'\theta)
\right]$](img87.png) |
(19) |
where in the second equation we must have ![]() . Since the right-hand
sides are real, we have the four real equations
. Since the right-hand
sides are real, we have the four real equations
![$\displaystyle \frac{1}{\pi}
\int_{-\pi}^{\pi}d\theta\,
\left[
\cos(k\theta)\cos(k'\theta)
+
\sin(k\theta)\sin(k'\theta)
\right]$](img88.png) |
|||
![$\displaystyle \frac{1}{\pi}
\int_{-\pi}^{\pi}d\theta\,
\left[
\sin(k\theta)\cos(k'\theta)
-
\cos(k\theta)\sin(k'\theta)
\right]$](img89.png) |
|||
![$\displaystyle \frac{1}{\pi}
\int_{-\pi}^{\pi}d\theta\,
\left[
\cos(k\theta)\cos(k'\theta)
-
\sin(k\theta)\sin(k'\theta)
\right]$](img90.png) |
|||
![$\displaystyle \frac{1}{\pi}
\int_{-\pi}^{\pi}d\theta\,
\left[
\sin(k\theta)\cos(k'\theta)
+
\cos(k\theta)\sin(k'\theta)
\right]$](img91.png) |
(20) |
where we must have ![]() in the last two equations. In the case
in the last two equations. In the case
![]() , which implies that
, which implies that ![]() and
and ![]() , we obtain from the first
equation the identity
, we obtain from the first
equation the identity
which is a part of the relations of orthogonality and norm of the Fourier
basis, namely the one giving the squared norm of the constant function
which is equal to one for all ![]() . The second equation is just a
trivial identity when we have
. The second equation is just a
trivial identity when we have ![]() and
and ![]() , which we may therefore
ignore. We may now assume that we have
, which we may therefore
ignore. We may now assume that we have ![]() for all the four
equations. Adding and subtracting the first and third equations we get
for all the four
equations. Adding and subtracting the first and third equations we get
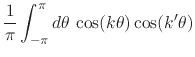 |
|||
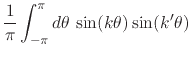 |
(22) |
for ![]() , while adding and subtracting the other two equations we get
, while adding and subtracting the other two equations we get
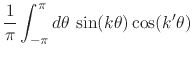 |
|||
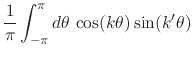 |
(23) |
for ![]() , which are just two copies of the same relation. We have
therefore the complete set of orthogonality relations, which also includes
those relations giving the norms of the basis functions,
, which are just two copies of the same relation. We have
therefore the complete set of orthogonality relations, which also includes
those relations giving the norms of the basis functions,
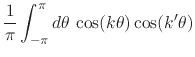 |
|||
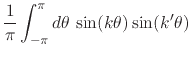 |
|||
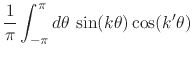 |
(24) |
where ![]() , which includes all the relevant cases, that is, all the
relevant pairs of elements of the basis in Equation (13),
except for the single case for
, which includes all the relevant cases, that is, all the
relevant pairs of elements of the basis in Equation (13),
except for the single case for ![]() and
and ![]() , which we examined
separately before, leading to Equation (21). Note that this
derivation included the determination of the form of the scalar product
for the basis elements. Given two integrable real functions
, which we examined
separately before, leading to Equation (21). Note that this
derivation included the determination of the form of the scalar product
for the basis elements. Given two integrable real functions ![]() and
and ![]() , their scalar product is given by
, their scalar product is given by
which induces a positive-definite norm in the space of all integrable real functions defined on the periodic interval, which is thus seen to constitute a Hilbert space. We may therefore conclude that the whole structure of orthogonality and norm of the Fourier basis is contained in the structure of the inner analytic function within the unit disk of the complex plane.
Note that, since all possible inner analytic functions are given by
convergent power series within the open unit disk, and since these power
series can be understood as infinite linear combinations of the particular
set of inner analytic functions given by the non-negative powers
![]() , we
may think that this set of functions forms a basis of the space of
inner analytic functions, which we may call the Taylor basis. Since
the orthogonality of the Fourier basis was obtained above from the
properties of this set of non-negative powers, it becomes clear that the
orthogonality of the Fourier basis is a consequence of similar properties
that must hold for the Taylor basis. In fact, it is possible to define a
complex scalar product within the space of inner analytic functions,
according to which this Taylor basis is orthogonal. Since this constitutes
a considerable detour from our main line of reasoning here, it will be
presented as an appendix. As one can see in Appendix A, this
complex scalar product induces in the space of inner analytic functions a
positive-definite norm. As was observed in [#!CAoRFI!#], this space forms
a vector space over the field of complex numbers, and we thus see that it
constitutes in fact a complex Hilbert space.
, we
may think that this set of functions forms a basis of the space of
inner analytic functions, which we may call the Taylor basis. Since
the orthogonality of the Fourier basis was obtained above from the
properties of this set of non-negative powers, it becomes clear that the
orthogonality of the Fourier basis is a consequence of similar properties
that must hold for the Taylor basis. In fact, it is possible to define a
complex scalar product within the space of inner analytic functions,
according to which this Taylor basis is orthogonal. Since this constitutes
a considerable detour from our main line of reasoning here, it will be
presented as an appendix. As one can see in Appendix A, this
complex scalar product induces in the space of inner analytic functions a
positive-definite norm. As was observed in [#!CAoRFI!#], this space forms
a vector space over the field of complex numbers, and we thus see that it
constitutes in fact a complex Hilbert space.