Next: Extension of the Theory Up: Complex Analysis of Real Previous: Completeness Relation
In this paper we have made the deliberate choice of not discussing the question of the convergence of Fourier series in any amount of detail, that is, we have not discussed any of the many existing so-called Fourier theorems. The reason for this is that we believe that this would constitute a rather long and complex discussion, best left for a separate paper. Instead, we have focused our attention on the summation rule given in Equation (12), according to which all Fourier series of integrable real functions, without any further restrictions, can be added up in such a way that one is able to recover the functions from their Fourier coefficients, even if the Fourier series themselves diverge. However, we may make a few comments about the issue of convergence, without going too far afield in that subject, in order to exhibit the relation between our complex analytic structure and the convergence problem.
First of all, let us recall that, as was shown in [#!CAoRFI!#], the real
function ![]() is equal almost everywhere to the real part of the
corresponding inner analytic function
is equal almost everywhere to the real part of the
corresponding inner analytic function ![]() , taken in the
, taken in the
![]() limit, and also that, as we have shown in Section 2 of
this paper, the Fourier series of
limit, and also that, as we have shown in Section 2 of
this paper, the Fourier series of ![]() is given by the real part of
the Taylor series
is given by the real part of
the Taylor series ![]() of
of ![]() in that same limit. Therefore, it is
clearly apparent that, as was already noted in Section 2, the
problem of the convergence of real Fourier series is completely identified
with the problem of the convergence of the corresponding complex power
series on the unit circle, including the cases in which it is the rim of
their maximum disks of convergence. Whatever is established for one type
of series is also valid for the other. As was also noted in
Section 2, the convergence properties on the unit circle will
depend on the existence and nature of the singularities of
in that same limit. Therefore, it is
clearly apparent that, as was already noted in Section 2, the
problem of the convergence of real Fourier series is completely identified
with the problem of the convergence of the corresponding complex power
series on the unit circle, including the cases in which it is the rim of
their maximum disks of convergence. Whatever is established for one type
of series is also valid for the other. As was also noted in
Section 2, the convergence properties on the unit circle will
depend on the existence and nature of the singularities of ![]() on that
circle.
on that
circle.
One way to discuss the issue of convergence is to observe that the
summation rule given in Equation (12) involves two limits,
one being the series summation limit and the other being the
![]() limit from the interior of the unit disk to the unit circle. What
has been shown so far in this series of papers is that if one takes the
series summation limit first, and only after that the
limit from the interior of the unit disk to the unit circle. What
has been shown so far in this series of papers is that if one takes the
series summation limit first, and only after that the
![]() limit, then it is always possible to recover the real function from its
Fourier coefficients. It is therefore immediately apparent that the
statement that the Fourier series converges over the unit circle is
equivalent to the statement that the order of these two limits can be
inverted. In fact, by first taking the
limit, then it is always possible to recover the real function from its
Fourier coefficients. It is therefore immediately apparent that the
statement that the Fourier series converges over the unit circle is
equivalent to the statement that the order of these two limits can be
inverted. In fact, by first taking the
![]() limit one obtains
the usual Fourier series over the unit circle, and if one is then able to
take the series summation limit, then that series converges to the
corresponding real function.
limit one obtains
the usual Fourier series over the unit circle, and if one is then able to
take the series summation limit, then that series converges to the
corresponding real function.
The general problem of deciding under what conditions the order of the two
limits can be inverted is not a simple one. However, it is not too
difficult to use our analytic structure to write the partial sums of the
Fourier series in terms of real integrals which are similar to the
Dirichlet integrals usually involved in some of the Fourier theorems.
This can then be used as the starting point for further discussions of the
convergence problem, including in particular discussions establishing the
connection of the analytic structure with specific Fourier theorems. In
order to do this, let ![]() be an integrable real function on
be an integrable real function on
![]() and let the real numbers
and let the real numbers ![]() ,
, ![]() and
and
![]() , for
, for
![]() , be its Fourier
coefficients. We may define the complex coefficients
, be its Fourier
coefficients. We may define the complex coefficients ![]() and
and ![]() shown in Equation (5), and thus construct the corresponding
inner analytic function
shown in Equation (5), and thus construct the corresponding
inner analytic function ![]() within the open unit disk, using the power
series
within the open unit disk, using the power
series ![]() given in Equation (6), which, as was shown
in [#!CAoRFI!#], always converges for
given in Equation (6), which, as was shown
in [#!CAoRFI!#], always converges for ![]() . The partial sums of the
first
. The partial sums of the
first ![]() terms of this series are given by
terms of this series are given by
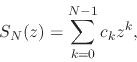 |
(34) |
a complex sequence which, for ![]() , we already know to converge to
, we already know to converge to
![]() in the
in the ![]() limit. Note however that, since
limit. Note however that, since ![]() is
in fact an analytic function over the whole complex plane, this expression
itself can be consistently considered for all
is
in fact an analytic function over the whole complex plane, this expression
itself can be consistently considered for all ![]() , and in particular for
, and in particular for
![]() on the unit circle, where
on the unit circle, where ![]() . Note also that the function
. Note also that the function ![]() may have singularities on the unit circle, but that these must be
integrable ones, at least along that circle. In addition to this, the
complex coefficients
may have singularities on the unit circle, but that these must be
integrable ones, at least along that circle. In addition to this, the
complex coefficients ![]() may be written as integrals involving
may be written as integrals involving ![]() ,
with the use of the Cauchy integral formulas,
,
with the use of the Cauchy integral formulas,
| (35) |
where ![]() can be taken as a circle centered at the origin, with radius
can be taken as a circle centered at the origin, with radius
![]() . The reason why we may include the case
. The reason why we may include the case ![]() here is
that, as was shown in [#!CAoRFI!#], as a function of
here is
that, as was shown in [#!CAoRFI!#], as a function of ![]() the
expression above for
the
expression above for ![]() is not only constant within the open unit
disk, but also continuous from within at the unit circle. In this way the
coefficients
is not only constant within the open unit
disk, but also continuous from within at the unit circle. In this way the
coefficients ![]() may be written back in terms of the inner analytic
function
may be written back in terms of the inner analytic
function ![]() . If we substitute this expression for
. If we substitute this expression for ![]() back in the
partial sums of the series we get
back in the
partial sums of the series we get
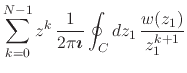 |
|||
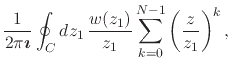 |
(36) |
where we must have ![]() . The sum is now a finite geometric
progression, so that we have
. The sum is now a finite geometric
progression, so that we have
A careful discussion of this formula is now in order. There are two
relevant cases to consider. In the first case we see that, if we have that
![]() , then in the first term above we obtain the expression of
the Cauchy integral formula for
, then in the first term above we obtain the expression of
the Cauchy integral formula for ![]() , which then allows us to write an
explicit expression for the remainder of the complex power series after
one adds up its first
, which then allows us to write an
explicit expression for the remainder of the complex power series after
one adds up its first ![]() terms,
terms,
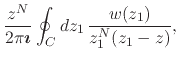 |
(38) |
where
![]() . This expression of the remainder in closed
form, an expression which, as one can easily show, goes to zero in the
. This expression of the remainder in closed
form, an expression which, as one can easily show, goes to zero in the
![]() limit, is what makes it easy to discuss the convergence of
complex power series. However, this expression does not give us an
equivalent expression for the remainder of the Fourier series, because
this would require us to make
limit, is what makes it easy to discuss the convergence of
complex power series. However, this expression does not give us an
equivalent expression for the remainder of the Fourier series, because
this would require us to make ![]() , which is not allowed by the
strict inequality
, which is not allowed by the
strict inequality ![]() , a restriction which is due to the use of
the Cauchy integral formulas. In the second case we observe that, if we
have that
, a restriction which is due to the use of
the Cauchy integral formulas. In the second case we observe that, if we
have that ![]() , then the first term in Equation (37)
is simply zero, and therefore we get a modified expression for the partial
sums of the series,
, then the first term in Equation (37)
is simply zero, and therefore we get a modified expression for the partial
sums of the series,
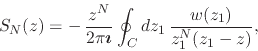 |
(39) |
where ![]() . Note that in this case we are unable to write an
explicit expression in closed form for the remainder of the series, a fact
which seems to be related to the remarkable difficulty in finding a
necessary and sufficient condition for the convergence of Fourier series.
Since
. Note that in this case we are unable to write an
explicit expression in closed form for the remainder of the series, a fact
which seems to be related to the remarkable difficulty in finding a
necessary and sufficient condition for the convergence of Fourier series.
Since ![]() may have any complex value in this expression, we may now make
may have any complex value in this expression, we may now make
![]() with
with ![]() , as well as
, as well as
![]() , and thus write the integral
explicitly in terms of the variable
, and thus write the integral
explicitly in terms of the variable ![]() on the circle of radius
on the circle of radius
![]() ,
,
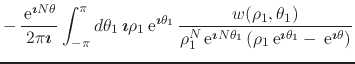 |
|||
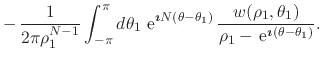 |
(40) |
Making
![]() we have
we have
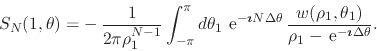 |
(41) |
In order to be able to write explicitly the real and imaginary parts of the partial sums, we must now rationalize this expression,
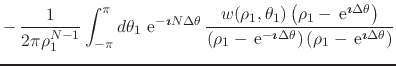 |
|||
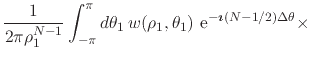 |
|||
 |
(42) |
The expression can be somewhat simplified if we write most things in terms
of
![]() , as well as in terms of
, as well as in terms of ![]() ,
,
![$\displaystyle \frac{1}{2\pi\rho_{1}^{N-1}}
\int_{-\pi}^{\pi}d\theta_{1}\,
\left...
...1},\theta_{1})
+
\mbox{\boldmath$\imath$}
v(\rho_{1},\theta_{1})
\right]
\times$](img168.png) |
|||
![$\displaystyle \hspace{7em}
\times
\left[
\rule{0em}{2.5ex}
\cos(N_{1}\Delta\theta)
-
\mbox{\boldmath$\imath$}
\sin(N_{1}\Delta\theta)
\right]
\times$](img169.png) |
(43) | ||
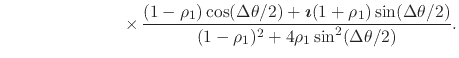 |
In this context, a Fourier theorem is one which states sufficient
conditions on ![]() under which it follows that the real part of the
corresponding sequence of partial sums
under which it follows that the real part of the
corresponding sequence of partial sums
![]() converges in the
converges in the
![]() limit, after one takes the
limit, after one takes the ![]() limit, so that the
integral is written over the unit circle. In any circumstances in which
one managed to calculate these integrals explicitly in terms of
limit, so that the
integral is written over the unit circle. In any circumstances in which
one managed to calculate these integrals explicitly in terms of
![]() , for
, for ![]() , one would then be able to consider taking
the
, one would then be able to consider taking
the ![]() limit of the resulting expression. However, despite
the facts that
limit of the resulting expression. However, despite
the facts that
![]() and that
and that
![]() , almost everywhere over the unit circle, as
well as the fact that these are integrable real functions, we cannot
simply take the
, almost everywhere over the unit circle, as
well as the fact that these are integrable real functions, we cannot
simply take the ![]() limit of this expression as it stands,
because it was derived under the hypothesis that
limit of this expression as it stands,
because it was derived under the hypothesis that ![]() , and
therefore that
, and
therefore that ![]() , which at this point implies the strict
inequality
, which at this point implies the strict
inequality ![]() . We may however put
. We may however put ![]() in the integrand
simply in order to simplify the integrals, so as to exhibit their
structure more clearly. If one does that one obtains
in the integrand
simply in order to simplify the integrals, so as to exhibit their
structure more clearly. If one does that one obtains
![\begin{displaymath}
\int_{-\pi}^{\pi}d\theta_{1}\,
\left[
\rule{0em}{2.5ex}
...
...2ex}(N-1/2)\Delta\theta\right]
}
{
\sin(\Delta\theta/2)
},
\end{displaymath}](img179.png) |
(44) |
which clearly reduces to Dirichlet integrals and other similar integrals. A more complete discussion of the issue of convergence would require considerable development of the ideas and structures involved in these arguments. It is currently not entirely clear how useful the analytic structure within the open unit disk can be in regards to proving known Fourier theorems or discovering new ones.