Next: Conclusions and Outlook Up: Complex Analysis of Real Previous: Notes on the Convergence
Up to this point we have been examining only the Fourier theory of
integrable real functions. In addition to this, a small extension of the
theory has already been considered when we wrote the Fourier expansion of
the Dirac delta ``function'' in Equations (27)
and (28) of Section 4, with the help of the
summation rule given in Equation (12). This ``function'' has
in common with the integrable real functions the fact that its Fourier
coefficients ![]() and
and ![]() are limited when we take the
limit
are limited when we take the
limit ![]() . The same is true for the corresponding complex Taylor
coefficients
. The same is true for the corresponding complex Taylor
coefficients ![]() in either case. However, the correspondence between
real Fourier coefficients and complex Taylor coefficients given by the
relations in Equation (5) can be generalized, independently
of any concerns about the behavior of these coefficients when
in either case. However, the correspondence between
real Fourier coefficients and complex Taylor coefficients given by the
relations in Equation (5) can be generalized, independently
of any concerns about the behavior of these coefficients when
![]() , and independently of any concerns about the convergence of
the corresponding series.
, and independently of any concerns about the convergence of
the corresponding series.
We will now discuss the extension of the Fourier theory beyond the realm
of integrable real functions. One way to look at this, which is probably
the most general possible way, is to simply consider the set of all
inner analytic functions. Given any inner analytic function ![]() and its complex Taylor series around the origin, which is therefore
convergent within the open unit disk, and irrespective of whether or not
and its complex Taylor series around the origin, which is therefore
convergent within the open unit disk, and irrespective of whether or not
![]() corresponds to an integrable real function, one can define a
corresponding real Fourier series on the unit circle. In all such cases
the issues of convergence of the resulting Fourier series are then
completely identified with the corresponding issues for the Taylor series
restricted to the unit circle, which is often the border of its maximum
disk of convergence. Important examples which are not related to
integrable real functions are the cases of the Dirac delta ``function''
and of its derivatives of all orders, which were discussed in detail
in [#!CAoRFII!#].
corresponds to an integrable real function, one can define a
corresponding real Fourier series on the unit circle. In all such cases
the issues of convergence of the resulting Fourier series are then
completely identified with the corresponding issues for the Taylor series
restricted to the unit circle, which is often the border of its maximum
disk of convergence. Important examples which are not related to
integrable real functions are the cases of the Dirac delta ``function''
and of its derivatives of all orders, which were discussed in detail
in [#!CAoRFII!#].
Another way to look at this issue is through the properties of the sets of
complex coefficients ![]() of the Taylor series. Given any set of
complex coefficients
of the Taylor series. Given any set of
complex coefficients ![]() , regardless of whether or not they follow
from a known inner analytic function, one can construct both a complex
power series
, regardless of whether or not they follow
from a known inner analytic function, one can construct both a complex
power series ![]() and the corresponding real coefficients
and the corresponding real coefficients ![]() and
and ![]() , using the relations in Equations (5)
and (6). In many cases the Fourier series generated by these
real coefficients will not converge, even if the complex power series
converges to an inner analytic function within the open unit disk.
However, if the complex power series is indeed convergent on that disk,
then one can discuss whether or not a real object can be defined on the
unit circle, through the
, using the relations in Equations (5)
and (6). In many cases the Fourier series generated by these
real coefficients will not converge, even if the complex power series
converges to an inner analytic function within the open unit disk.
However, if the complex power series is indeed convergent on that disk,
then one can discuss whether or not a real object can be defined on the
unit circle, through the
![]() limit from the open unit disk,
for example using the summation rule for Fourier series given in
Equation (12).
limit from the open unit disk,
for example using the summation rule for Fourier series given in
Equation (12).
If we examine that summation rule, it is apparent that it will work for
much more than just integrable real functions, which always have bounded
Fourier coefficients. For example, one may have unbounded Fourier
coefficients ![]() and
and ![]() , such as those of the
, such as those of the ![]() derivative of the delta ``function'', which diverge to infinity as
the power
derivative of the delta ``function'', which diverge to infinity as
the power ![]() when
when ![]() , and still have a well-defined inner
analytic function, as was shown in detail in [#!CAoRFII!#]. In fact, one
can show that the summation rule can be used for all sets of Fourier
coefficients that do not diverge exponentially fast with
, and still have a well-defined inner
analytic function, as was shown in detail in [#!CAoRFII!#]. In fact, one
can show that the summation rule can be used for all sets of Fourier
coefficients that do not diverge exponentially fast with ![]() . In
order to develop this idea, let us first define a very general condition
on the sequences of complex coefficients that guarantees that the
corresponding power series are convergent within the open unit disk, and
thus converge to inner analytic functions.
. In
order to develop this idea, let us first define a very general condition
on the sequences of complex coefficients that guarantees that the
corresponding power series are convergent within the open unit disk, and
thus converge to inner analytic functions.
Given an arbitrary ordered set of complex coefficients ![]() , for
, for
![]() , if they satisfy the condition that
, if they satisfy the condition that
for all real ![]() , then we say that the sequence of coefficients
, then we say that the sequence of coefficients ![]() is exponentially bounded.
is exponentially bounded.
What this means is that ![]() may or may not go to zero as
may or may not go to zero as ![]() ,
may approach a non-zero complex number, and may even diverge to infinity
as
,
may approach a non-zero complex number, and may even diverge to infinity
as ![]() , so long as it does not do so exponentially fast. This
includes therefore not only the sequences of complex Taylor coefficients
corresponding to all possible convergent Fourier series, but many
sequences that correspond to Fourier series that diverge almost
everywhere. Also, it not only includes the sequences of complex Taylor
coefficients corresponding to all possible integrable real functions, but
many sequences of coefficients that cannot be obtained at all from a real
function, such as those associated to the Dirac delta ``function'' and its
derivatives of arbitrarily high orders, as was shown in [#!CAoRFII!#]. We
see therefore that this is a very weak condition on the complex sequence
of coefficients
, so long as it does not do so exponentially fast. This
includes therefore not only the sequences of complex Taylor coefficients
corresponding to all possible convergent Fourier series, but many
sequences that correspond to Fourier series that diverge almost
everywhere. Also, it not only includes the sequences of complex Taylor
coefficients corresponding to all possible integrable real functions, but
many sequences of coefficients that cannot be obtained at all from a real
function, such as those associated to the Dirac delta ``function'' and its
derivatives of arbitrarily high orders, as was shown in [#!CAoRFII!#]. We
see therefore that this is a very weak condition on the complex sequence
of coefficients ![]() .
.
Before we proceed to the extension of the Fourier theory, let us establish
a preliminary result, which can be understood as a property of the
sequences of complex coefficients ![]() which satisfy the condition
stated in Definition 1. We will show that the condition
expressed in Equation (45) implies an infinite collection of
other similar conditions involving the
which satisfy the condition
stated in Definition 1. We will show that the condition
expressed in Equation (45) implies an infinite collection of
other similar conditions involving the ![]() limit, that express
modified bounds on these sequences of coefficients.
limit, that express
modified bounds on these sequences of coefficients.
for all real ![]() and for all real powers
and for all real powers ![]() .
.
This is just a formalization of the well-known fact that the
negative-exponent real exponential function of ![]() goes to zero faster
than any positive real power of
goes to zero faster
than any positive real power of ![]() goes to infinity, as
goes to infinity, as ![]() . In
order to prove this, we observe that for
. In
order to prove this, we observe that for ![]() we may write the function
of
we may write the function
of ![]() on the left-hand side of Equation (46) as
on the left-hand side of Equation (46) as
| (47) |
Note that this is a positive real quantity. Recalling the properties of
the real logarithm function, we now observe that, given an arbitrary real
number ![]() , there is always a sufficiently large finite value
, there is always a sufficiently large finite value ![]() of
of
![]() above which
above which ![]() . Due to this we may write, for all
. Due to this we may write, for all ![]() ,
,
| (48) |
since the exponential with a strictly positive real exponent is a
monotonically increasing function. If we now choose ![]() , which we
may do because this value is positive and not zero, we get that, for all
, which we
may do because this value is positive and not zero, we get that, for all
![]() ,
,
| (49) |
According to our hypothesis about the coefficients ![]() , the
, the
![]() limit of the expression in the right-hand side is zero for
any strictly positive value of
limit of the expression in the right-hand side is zero for
any strictly positive value of ![]() , so that taking the
, so that taking the ![]() limit we establish our preliminary result,
limit we establish our preliminary result,
| (50) |
for all real ![]() and all real
and all real ![]() . Therefore, we have established this
property.
. Therefore, we have established this
property.
Let us now show that the condition that the sequence of complex
coefficients ![]() in Equation (5) is exponentially bounded
is equivalent to the condition that the sequences of real coefficients
in Equation (5) is exponentially bounded
is equivalent to the condition that the sequences of real coefficients
![]() and
and ![]() are both exponentially bounded. First, if we
assume that the sequences
are both exponentially bounded. First, if we
assume that the sequences ![]() and
and ![]() are both
exponentially bounded, and since from Equation (5) we have
that
are both
exponentially bounded, and since from Equation (5) we have
that
| (51) |
it follows at once that
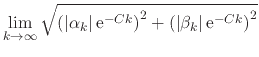 |
|||
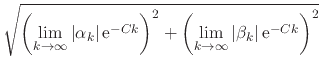 |
|||
| (52) |
since both limits in the right-hand side are zero, thus establishing that
the sequence ![]() is exponentially bounded. Second, if we assume that
the sequence
is exponentially bounded. Second, if we assume that
the sequence ![]() is exponentially bounded, and since from
Equation (5) we have that
is exponentially bounded, and since from
Equation (5) we have that
| (53) |
taking the ![]() limit and using the assumed property of the
sequence of coefficients
limit and using the assumed property of the
sequence of coefficients ![]() it follows that
it follows that
| (54) |
thus establishing that the sequence ![]() is exponentially bounded.
Clearly, an identical argument can be made for the sequence
is exponentially bounded.
Clearly, an identical argument can be made for the sequence ![]() .
This establishes that the statement that the sequence of complex
coefficients
.
This establishes that the statement that the sequence of complex
coefficients ![]() is exponentially bounded is equivalent to the
statement that the sequences of real coefficients
is exponentially bounded is equivalent to the
statement that the sequences of real coefficients ![]() and
and
![]() are both exponentially bounded.
are both exponentially bounded.
Let us now prove the following theorem about the convergence of the power
series constructed out of a given arbitrary sequence of complex
coefficients ![]() .
.
Given the arbitrary sequence of complex coefficients ![]() , we may
construct the complex power series in the complex
, we may
construct the complex power series in the complex ![]() plane, just as we
did in [#!CAoRFI!#],
plane, just as we
did in [#!CAoRFI!#],
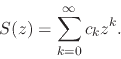 |
(55) |
We will first show that, if the sequence of coefficients ![]() is
exponentially bounded, then this series is absolutely convergent inside
the open unit disk, which then implies that it is simply convergent there.
is
exponentially bounded, then this series is absolutely convergent inside
the open unit disk, which then implies that it is simply convergent there.
In order to prove that ![]() is absolutely convergent, we consider the
real power series
is absolutely convergent, we consider the
real power series
![]() of the absolute values of the terms of
that series, which we write as
of the absolute values of the terms of
that series, which we write as
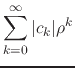 |
|||
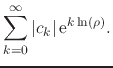 |
(56) |
Since ![]() inside the open unit disk, the logarithm shown is strictly
negative, and we may put
inside the open unit disk, the logarithm shown is strictly
negative, and we may put ![]() with real
with real ![]() . We can now see
that, according to our hypothesis about the coefficients
. We can now see
that, according to our hypothesis about the coefficients ![]() , the
terms of this series go to zero as
, the
terms of this series go to zero as ![]() ,
,
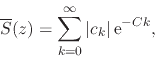 |
(57) |
since ![]() is real and strictly positive. In order to establish the
convergence of this real series, we write
is real and strictly positive. In order to establish the
convergence of this real series, we write
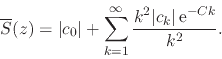 |
(58) |
According to the property expressed in Equation (46), with
![]() , the numerator shown above goes to zero as
, the numerator shown above goes to zero as ![]() , and
therefore above a sufficiently large value
, and
therefore above a sufficiently large value ![]() of
of ![]() it is less that
one, so that we may write that
it is less that
one, so that we may write that
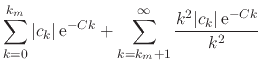 |
|||
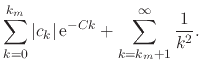 |
(59) |
The first term on the right-hand side is a finite sum and therefore is
finite, and the second term can be bounded from above by a convergent
asymptotic integral on ![]() , so that we have
, so that we have
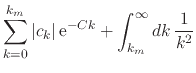 |
|||
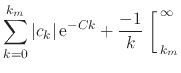 |
|||
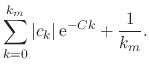 |
(60) |
This last expression is therefore a finite upper bound for all the partial
sums of the series
![]() . It follows that
. It follows that
![]() ,
which is a real sum of positive terms, so that its partial sums form a
monotonically increasing real sequence which is now found to be bounded
from above, is therefore convergent. It then follows that
,
which is a real sum of positive terms, so that its partial sums form a
monotonically increasing real sequence which is now found to be bounded
from above, is therefore convergent. It then follows that ![]() is
absolutely convergent and therefore convergent. Since this is valid for
all
is
absolutely convergent and therefore convergent. Since this is valid for
all ![]() , we may conclude that
, we may conclude that ![]() converges on the open unit
disk. This completes the proof of Theorem 2.
converges on the open unit
disk. This completes the proof of Theorem 2.
Since the series ![]() considered above is a convergent power series
within the open unit disk, it converges to an analytic function
considered above is a convergent power series
within the open unit disk, it converges to an analytic function ![]() in
that domain, which is therefore an inner analytic function. We therefore
conclude that, if the sequence of complex coefficients
in
that domain, which is therefore an inner analytic function. We therefore
conclude that, if the sequence of complex coefficients ![]() in
Equation (5) is exponentially bounded, then it is the set of
Taylor coefficients of an inner analytic function. It now follows that, if
the corresponding Fourier coefficients
in
Equation (5) is exponentially bounded, then it is the set of
Taylor coefficients of an inner analytic function. It now follows that, if
the corresponding Fourier coefficients ![]() and
and ![]() are
both exponentially bounded, then the corresponding complex coefficients
are
both exponentially bounded, then the corresponding complex coefficients
![]() are also exponentially bounded, and therefore the corresponding
Fourier series can be regulated by the use of the summation rule in
Equation (12). Unless the Fourier coefficients go to zero as
are also exponentially bounded, and therefore the corresponding
Fourier series can be regulated by the use of the summation rule in
Equation (12). Unless the Fourier coefficients go to zero as
![]() , the Fourier series on the unit circle is sure to diverge
almost everywhere. One can then consider defining the corresponding real
object on the unit circle using the
, the Fourier series on the unit circle is sure to diverge
almost everywhere. One can then consider defining the corresponding real
object on the unit circle using the
![]() limit from the open
unit disk, for example through the use of the summation rule for the
Fourier series, given in Equation (12).
limit from the open
unit disk, for example through the use of the summation rule for the
Fourier series, given in Equation (12).
In this way the Fourier theory of integrable real functions on the unit
circle can be extended to a much larger set of real objects, including for
example all the singular distributions discussed in [#!CAoRFII!#], as
well as the examples of non-integrable real functions mentioned in that
paper. In fact, this extension of the Fourier theory includes a large
class of non-integrable real functions, as will be shown in the fourth
paper of this series. In this extended Fourier theory the real objects can
be considered as representable directly by their sequences of Fourier
coefficients, even when the corresponding Fourier series diverge. All
operations involving these divergent Fourier series can be mapped to
absolutely and uniformly convergent series and analytic operations within
the open unit disk, whose results are then taken to the unit circle
through the use of the
![]() limit. In many simple cases the
mere values of the real objects on the unit circle will be recovered in
this way, and in other more abstract cases global properties of the real
objects may be obtained in this way, such as in the case of the Dirac
delta ``function'' and its derivatives of all orders, as was discussed in
detail in [#!CAoRFII!#].
limit. In many simple cases the
mere values of the real objects on the unit circle will be recovered in
this way, and in other more abstract cases global properties of the real
objects may be obtained in this way, such as in the case of the Dirac
delta ``function'' and its derivatives of all orders, as was discussed in
detail in [#!CAoRFII!#].