Programas mcrelaxer e mcsampler

Os programas mcrelaxer e mcsampler geram as configurações do campo para acúmulo dos observáveis. A estrutura geral dos dois programas é a mesma, mas eles apresentam algumas diferenças relacionadas com as suas necessidades específicas. Existem dois loops centrais. O externo está relacionado com a quantidade de submédias desejadas para o cálculo estatístico (naver). O mais interno está relacionado com o número de iterações efetuadas em cada uma das submédias (niter). Os valores destas duas variáveis encontram-se no arquivo inp.dat.

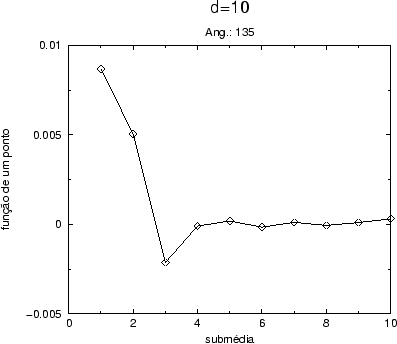
O programa mcrelaxer tem como objetivo gerar, a partir de uma configuração inicial dos campos, escolhida arbitrariamente na rede, uma configuração dos campos relaxada, necessária para a tomada dos dados. Um forma de medir a relaxação do campo é olhando para a função de um ponto $\langle\varphi\rangle$ , que deve ser constante para um campo relaxado. A figura (B.1) ilustra este comportamento.

**Figure:** Valor esperado do campo medido por simulação como função da submédia executada, para a teoria interagente com raio unitário e ângulo $\theta =135^0$ .
$\begin{figure}\centering\epsfig{file=ps/relax.epsf,scale=0.5,angle=0} \end{figure}$

Como este programa é relativamente rápido não é preciso nenhuma forma de paralelização.

O programa mcsampler gera, a partir de uma configuração relaxada do campo, as configurações necessárias para a medida dos observáveis. Assim sendo, ele é bem mais demorado que o mcrelaxer e torna-se, portanto, importante o uso de paralelização. Esta é uma diferença básica entre os dois programas.

**Figure B.2:** Estrutura geral dos programa `mcsampler` e `mcrelaxer.`
$\begin{figure}\centering\epsfig{file=ps/estrutura.fps,scale=0.9,angle=0} \end{figure}$

A subrotina initialize, como o próprio nome já diz, inicializa alguns parâmetros, como o valor de $\pi$ , o seu dobro, o valor do momento na rede (mplatt), entre outros. A rotina também inicializa alguns flags relacionados com a dimensionalidade da rede e principalmente, guarda em matrizes as fases da transformada de Fourier do campo para o espaço de momentos.

Para calcular as transformadas de Fourier do campo $\varphi(\vec{n})$ , precisamos calcular expressões do tipo

$\begin{displaymath} \varphi(\vec{n}) e^{\frac{2 \pi}{N} \vec{k}.\vec{n}} = \varp... ...ec{n}} + \imath \sin{\frac{2 \pi}{N} \vec{k}.\vec{n}} \right]. \end{displaymath}$

Os cossenos são armazenados na matriz phase() e os senos na matriz phaux(). Note que $\vec{k}.\vec{n}$ assume valores entre -dN²/2 e +dN²/2, porém sem percorrer todos os seus inteiros. Por simplicidade de código armazenamos somente as componentes positivas destas fases.

A subrotina indexer lineariza a rede d-dimensional preservando porém a estrutura de vizinhos, utilizada nos algoritmos de geração do campo. Os sítios são classificados em black e white como em um tabuleiro de xadrez.

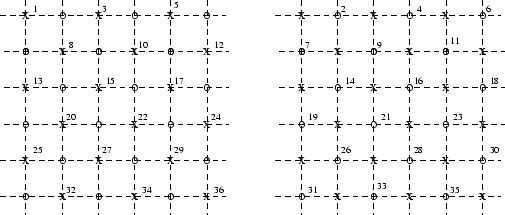
Como exemplo vamos considerar uma rede com d=2 e N=6. A rede é indexada através do índice ind, indo de 1 a 36, conforme a figura (B.3).

**Figure:** Estrutura de indexação da rede para o caso de N=6 e d=2.
$\begin{figure}\centering\epsfig{file=ps/rede1.ps,scale=0.8,angle=0} \end{figure}$

Os sítios com círculo são ditos white e os com cruzes, black. São criadas duas estruturas de indexação auxiliares (fig. (B.4)) expressas através de dois vetores: indwhite() e indblack(). Neste caso, portanto, temos indwhite(1)=2, indwhite(2)=4, indwhite(3)=6 etc. e indblack(1)=1, indblack(2)=3, indblack(3)=5 etc.

**Figure:** Estruturas auxiliares de indexação da rede utilizadas nos algoritmos de geração das configurações dos campos.
$\begin{figure}\centering\epsfig{file=ps/rede2.ps,scale=0.8,angle=0} \end{figure}$

Precisamos ainda de vetores que carreguem informação a respeito da estrutura de primeiros vizinhos. Assim temos o vetor neighbor(i,j) de maneira que neighbor(1,1)=6, neighbor(1,2)=2, neighbor(1,3)=31, neighbor (1,4)=7 expressam os vizinhos nas 4 direções bi-dimensionais no sítio 1 da rede completa. Estruturas análogas são desenvolvidas para as redes black e white.

A subrotina também define um array associado com as transformadas de Fourier do campo, o indphase(msite,imode). A idéia é armazenar variáveis inteiras que funcionam como ponteiros para locais de memória onde estão calculadas as fases de Fourier. Para entender melhor este procedimento, vamos considerar uma rede bidimensional com 4 sítios em cada direção. O índice imode representa os modos de Fourier que são calculados. Neste código calculamos somente os modos com todas as componentes de Fourier positivas. Assim, o array indphase contém

e assim sucessivamente até imode=8, representando o oitavo modo de Fourier calculado. Conforme veremos na subrotina transform, este array é utilizado para calcular as transformadas de Fourier do campo nos modos selecionados.

A subrotina transform calcula as transformadas de Fourier do campo, definidas a partir de (3.6). Como exemplo, vamos considerar novamente d=2 e N=4. Neste caso o modo zero é definido como

$\begin{displaymath} \tilde{\varphi}(\vec{0}) = \frac{1}{N^d} \sum_{\rm {isite}} \varphi({\rm {isite}}), \end{displaymath}$

onde o índice isite percorre todos os sítios da rede. No código este modo é expresso como $\tilde{\varphi}(1,0) = {\rm ftrnr}(1,0) + \imath {\rm ftrni}(1,0)$ onde

$\begin{displaymath} {\rm ftrnr}(1,0)=\frac{1}{N^d} \sum_{\rm {isite}} {\rm phase}({\rm indphase}({\rm {isite}},0)) \varphi({\rm {isite}}) \end{displaymath}$

$\begin{displaymath} {\rm ftrni}(1,0)=\frac{1}{N^d} \sum_{\rm {isite}} {\rm phaux}({\rm indphase}({\rm {isite}},0)) \varphi({\rm {isite}}), \end{displaymath}$

A subrotina accumulate acumula os observáveis preliminares. Para entender o seu funcionamento lembremo-nos que os observáveis do modelo são expressos por uma integração funcional que pode ser entendida como uma soma dos observáveis em cada uma das infinitas possibilidades de configuração dos campos, ponderada pelo ``peso estatístico'' $e^{-S[\varphi]}$ . Os algoritmos de geração dos campos são efetuados nas rotinas cluster e sweeper e garantem uma coleção de configurações com distribuição dada pelo peso certo.

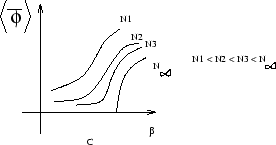
Em redes finitas o valor esperado do campo é nulo para qualquer valor de beta mesmo em modelos onde há quebra espontânea de simetria (QES). O mecanismo de transição de fases aparece somente no limite do contínuo conforme a figura (B.5).

**Figure:** Valor esperado da média do campo nos sítios como função de $\beta$ com (a) N finito e (b) $N\rightarrow \infty$ .
$\begin{figure}\centering\epsfig{file=ps/qes1.ps,scale=0.8,angle=0} \end{figure}$

Gostaríamos de obter um comportamento similar a (B.5.b) já em redes finitas. Porém sabemos que nestes modelos quando se introduz uma fonte externa temos apresentado na figura (B.6) no limite da fonte externa tendendo a zero.

**Figure:** Comportamento do parâmetro de ordem com a introdução de fontes externas, no limite de fontes indo a zero.
$\begin{figure}\centering\epsfig{file=ps/qes2.ps,scale=0.8,angle=0} \end{figure}$

A idéia então é forçar um comportamento tipo (B.6) mesmo sem fontes externas. Lembrando que as fontes externas introduzem no sistema uma direção preferencial, podemos fixar uma direção de quebra de simetria (por convenção a última) através do mecanismo que denominamos back rotation. Através dele rodamos $\langle\varphi\rangle$ na direção do último eixo de simetria interna. Desta maneira um modelo com simetria SO(3) por exemplo passa a ter simetria SO(2).

Além disso, fazemos um random twist, para ocupar melhor o espaço de configurações e desta maneira melhorar a função de autocorrelação. Por exemplo, para modelos com simetria SO(2), fazemos uma rotação $\gamma$ de todos os campos juntos em cada configuração.