Next: The Transform and its Up: Fourier Modes of a Previous: Organizing the Degrees of
For the position-space representation
![]() of the field,
with
of the field,
with
![]() and
and
![]() , one can index the field
into a single
, one can index the field
into a single ![]() -dimensional vector, using the single index
-dimensional vector, using the single index ![]() instead of all the position coordinates, where
instead of all the position coordinates, where
Defined in this way the index ![]() runs from
runs from ![]() to
to ![]() , thus
enumerating all the sites of the lattice. There is also an algorithm to
obtain the components of
, thus
enumerating all the sites of the lattice. There is also an algorithm to
obtain the components of ![]() back from the value of
back from the value of ![]() , as we
will discuss later. We would like to do the same for the momentum-space
representation
, as we
will discuss later. We would like to do the same for the momentum-space
representation
![]() , with
, with
![]() ,
,
![]() , where the extremes of the range are defined as
, where the extremes of the range are defined as
for odd ![]() , and as
, and as
for even ![]() . In order for the index value of
. In order for the index value of ![]() to correspond to the
zero mode
to correspond to the
zero mode
![]() , we would like to use the index
, we would like to use the index ![]() given by
given by
In order to show that one can in fact do this, and to discover how to
invert the relation, getting the components of ![]() out of
out of ![]() ,
we start with a version of the momentum-space index just like the
position-space one,
,
we start with a version of the momentum-space index just like the
position-space one,
which ranges from ![]() to
to ![]() and where
and where
![]() ,
,
![]() , just like the position-space index. Now, starting
from this index we have
, just like the position-space index. Now, starting
from this index we have
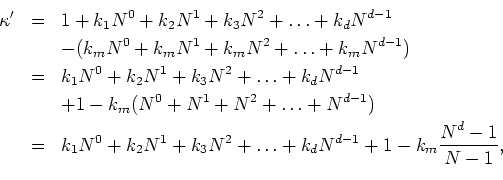
where ![]() is always divisible by
is always divisible by ![]() , of course. Therefore,
considering the definition of
, of course. Therefore,
considering the definition of ![]() , we have
, we have
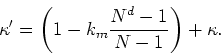
Since the two indices are related by an additive constant, either one can
be used to index the modes. Since ![]() ranges from
ranges from ![]() to
to ![]() ,
we have for the extreme values of
,
we have for the extreme values of ![]()
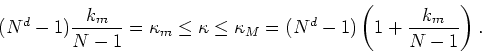
Note that ![]() is negative, so that the lower extreme is negative. For
odd
is negative, so that the lower extreme is negative. For
odd ![]() the extremes can be written explicitly as
the extremes can be written explicitly as
and the range is therefore symmetrical around ![]() . Note that since
. Note that since ![]() is
odd so is
is
odd so is ![]() , and therefore
, and therefore ![]() is even and thus divisible by
is even and thus divisible by
![]() . For even
. For even ![]() we get
we get
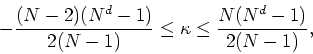
so that in this case the range is not symmetrical, and there are
![]() more positive-index elements than negative-index
elements. A little analysis will show that the integer divisions are
exact in this case also, without any truncation: since
more positive-index elements than negative-index
elements. A little analysis will show that the integer divisions are
exact in this case also, without any truncation: since ![]() is
always divisible by
is
always divisible by ![]() , we are left with
, we are left with ![]() and
and ![]() to be
considered, and since
to be
considered, and since ![]() is even both
is even both ![]() and
and ![]() are divisible by
are divisible by
![]() .
.
If we recall our organization of real and imaginary parts as independent
coordinates, as described in the previous section, it is interesting to
observe that one can verify that for odd ![]() the negative values of
the negative values of
![]() correspond to imaginary parts, the value
correspond to imaginary parts, the value ![]() to the real mode,
and the positive values to real parts. However, the same is not
true for even
to the real mode,
and the positive values to real parts. However, the same is not
true for even ![]() , due to the modes with one or more components equal to
, due to the modes with one or more components equal to
![]() , some of which have their imaginary parts at positive values of the
index. Due to this, in general it will be necessary to implement an
additional pair of indexing arrays in order to map real parts to the
corresponding imaginary parts and vice-versa, whenever it becomes
necessary to recover the two parts of one and the same mode.
, some of which have their imaginary parts at positive values of the
index. Due to this, in general it will be necessary to implement an
additional pair of indexing arrays in order to map real parts to the
corresponding imaginary parts and vice-versa, whenever it becomes
necessary to recover the two parts of one and the same mode.
It remains for us to discuss the inversion algorithm. The algorithm for
extracting the position coordinates ![]() from the position-space
index
from the position-space
index ![]() works by integer division, with truncation, and in
works by integer division, with truncation, and in ![]() dimensions is given by
dimensions is given by
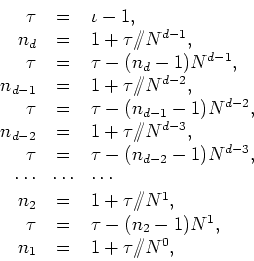
where ![]() is a temporary variable. It is therefore clear that we can
use exactly the same algorithm for extracting the
is a temporary variable. It is therefore clear that we can
use exactly the same algorithm for extracting the ![]() shifted momentum
coordinates
shifted momentum
coordinates
![]() from the index
from the index ![]() . Since
. Since ![]() and
and ![]() are related by an additive constant, we can also use the
algorithm for
are related by an additive constant, we can also use the
algorithm for ![]() , so long as we start by adding to it the constant
, so long as we start by adding to it the constant
![]() , and substitute
, and substitute ![]() by
by ![]() in the
formulas, in order to get the components
in the
formulas, in order to get the components ![]() of
of ![]() , and
therefore we have the algorithm
, and
therefore we have the algorithm
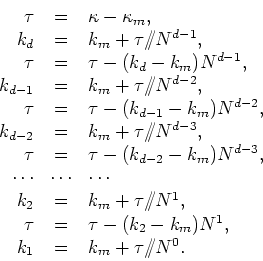
This completes the discussion of the indexing scheme in momentum space.