Next: Fortran Routines Up: Fourier Modes of a Previous: Indexing in Momentum Space
Let us discuss now, in detail, how to implement numerically the finite Fourier transform and its inverse transform. The complete Fourier transform of a real scalar field is given by
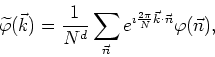
but we will only calculate and store the independent real and imaginary
parts,
![]() , which are given
by
, which are given
by
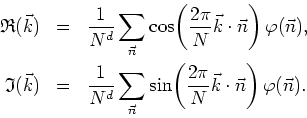
For use in the numerical programs we will implement these in matrix form,
using a single (usually very large)
![]() transformation
matrix,
transformation
matrix,
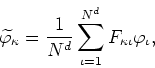
where
![]() stands for either a real part or an imaginary
part, depending on the value of the index
stands for either a real part or an imaginary
part, depending on the value of the index ![]() , according to our
classification of the independent variables in momentum space, and where,
accordingly,
, according to our
classification of the independent variables in momentum space, and where,
accordingly,
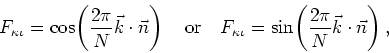
where ![]() corresponds to
corresponds to ![]() and
and ![]() to
to ![]() via the
respective indexation schemes. Since
via the
respective indexation schemes. Since
![]() has a limited
set of possible values, much smaller than the number of elements
has a limited
set of possible values, much smaller than the number of elements ![]() of
of
![]() , and which will be used repeatedly for many
different modes, in order to save both computation time and memory, we
will calculate all necessary sine and cosine functions just once,
beforehand, for future repeated use. We will store these values in a
relatively small array
, and which will be used repeatedly for many
different modes, in order to save both computation time and memory, we
will calculate all necessary sine and cosine functions just once,
beforehand, for future repeated use. We will store these values in a
relatively small array ![]() indexed by the integer
indexed by the integer
![]() , and construct a very large indexing matrix
, and construct a very large indexing matrix
![]() , of size
, of size
![]() , to pick up the
necessary values of
, to pick up the
necessary values of ![]() for each combination of a mode in momentum
space and a site in position space. Since this indexing matrix can be of
for each combination of a mode in momentum
space and a site in position space. Since this indexing matrix can be of
![]() -byte integers rather than of the
-byte integers rather than of the ![]() -byte double-precision real
numbers needed for the values of
-byte double-precision real
numbers needed for the values of ![]() , in this way we save memory at
the ratio of almost four to one. The range of the integer
, in this way we save memory at
the ratio of almost four to one. The range of the integer
![]() is given by
is given by
so that the size of the small double-precision array is given by
![]() , where
, where
![]() for either odd or even
for either odd or even
![]() , so that the size of this array is
, so that the size of this array is ![]() , of the order of
, of the order of
![]() , much smaller than
, much smaller than ![]() for the values of
for the values of ![]() of most
interest, from
of most
interest, from ![]() to
to ![]() . When we deal with the values of
. When we deal with the values of ![]() using this array, not all values along the array are actually going to be
used, because not all integers in the range can in fact be written as
using this array, not all values along the array are actually going to be
used, because not all integers in the range can in fact be written as
![]() . However, it can be verified that the rate of
useful occupation of the array is large for the dimensions of interest,
in fact, it is over
. However, it can be verified that the rate of
useful occupation of the array is large for the dimensions of interest,
in fact, it is over ![]() for dimensions from
for dimensions from ![]() to
to ![]() .
Therefore, we have here only a very small waste of memory space, and in
the interest of simplicity it is not worth while to try to improve this
occupation rate.
.
Therefore, we have here only a very small waste of memory space, and in
the interest of simplicity it is not worth while to try to improve this
occupation rate.
Since we must store the values of both the sines and the cosines, we actually have to double the size of the array as it was described above. In order to put the cosines at positive values of the index and the sines at negative values, we add and subtract constants in order to use the ranges that follow,
to be used for the sines, and
to be used for the cosines, so that the total range is given by
The total size of the array is now given by ![]() , which is
still much smaller than the indexing matrix. The indexing matrix
, which is
still much smaller than the indexing matrix. The indexing matrix
![]() will return the values of
will return the values of ![]() in this range, and
is to be used as the argument of
in this range, and
is to be used as the argument of ![]() , given values of
, given values of ![]() and
and
![]() , so that we have
, so that we have
and the transformation can now be written as
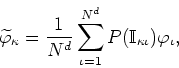
which includes all the independent real and imaginary parts, depending on
the values of ![]() , in a single matrix operation, which is easy to
implement efficiently.
, in a single matrix operation, which is easy to
implement efficiently.
Let us now examine the situation concerning the inverse transform. It is
clear that a similar scheme should be used for it. Since the indexing
matrix
![]() is so large, and considering the possibility
that a single program might need to use both the transform and its
inverse, it is important to build the scheme for the inverse transform in
such a way that it is able to use the same indexing matrix. As we will
see, it is possible to do this, but unfortunately not in a very efficient
way. For speed of execution the order of the indices matters, and should
in fact be
is so large, and considering the possibility
that a single program might need to use both the transform and its
inverse, it is important to build the scheme for the inverse transform in
such a way that it is able to use the same indexing matrix. As we will
see, it is possible to do this, but unfortunately not in a very efficient
way. For speed of execution the order of the indices matters, and should
in fact be
![]() for the direct transform and
for the direct transform and
![]() for the inverse transform. Hence, one can save memory
only so long as one needs only one of the two matrices or so long as the
program is not dependent on the performance of one of the two
transforms. The inverse Fourier transform is defined by
for the inverse transform. Hence, one can save memory
only so long as one needs only one of the two matrices or so long as the
program is not dependent on the performance of one of the two
transforms. The inverse Fourier transform is defined by
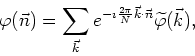
or, in ![]() -dimensional matrix form,
-dimensional matrix form,
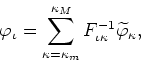
where the limits of the sum over the momentum index are
![]() and
and
![]() . We must now deal explicitly with
the fact that both the Fourier component of the field and the mode
function are complex. Since we have the decomposition of the field
. We must now deal explicitly with
the fact that both the Fourier component of the field and the mode
function are complex. Since we have the decomposition of the field
![]() , as well as
, as well as
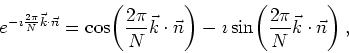
it follows that we have
![\begin{eqnarray*}
\varphi(\vec{n}) & = & \sum_{\vec{k}}\left[
\cos\!\left(\frac{...
...2\pi}{N}\vec{k}\cdot\vec{n}\right)\mathfrak{I}(\vec{k}) \right].
\end{eqnarray*}](img128.gif)
Since the field
![]() is real, the sum giving its imaginary
part must vanish, and we are left with
is real, the sum giving its imaginary
part must vanish, and we are left with
![\begin{displaymath}
\varphi(\vec{n})=\sum_{\vec{k}}\left[
\cos\!\left(\frac{2\pi...
...pi}{N}\vec{k}\cdot\vec{n}\right)\mathfrak{I}(\vec{k}) \right].
\end{displaymath}](img129.gif)
We must now consider separately the contributions to the sum from the real and complex modes. From the purely real modes we get the contributions
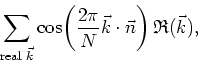
while from the complex modes we get the contributions
![\begin{displaymath}
\sum_{\mbox{\scriptsize complex }\vec{k}}\left[
\cos\!\left(...
...pi}{N}\vec{k}\cdot\vec{n}\right)\mathfrak{I}(\vec{k}) \right].
\end{displaymath}](img131.gif)
Since we keep only one copy of each independent
![]() and one
copy of each independent
and one
copy of each independent
![]() , while the sum above runs over
both parts on all the complex modes, in the case of these modes we must
multiply the contribution by a factor of two. In this way we get the
correct result when we run over the modes and use only the part which is
stored in each one. So in reality we will calculate this contribution as
, while the sum above runs over
both parts on all the complex modes, in the case of these modes we must
multiply the contribution by a factor of two. In this way we get the
correct result when we run over the modes and use only the part which is
stored in each one. So in reality we will calculate this contribution as
![\begin{displaymath}
\sum_{\mbox{\scriptsize complex }\vec{k}}\left[
2\cos\!\left...
...pi}{N}\vec{k}\cdot\vec{n}\right)\mathfrak{I}(\vec{k})
\right].
\end{displaymath}](img134.gif)
These factors of two, which do not appear in the real modes, prevent us from implementing the inverse transform as a single matrix operation. The best way to implement it will be to first perform a complete matrix operation with the factors of two for all modes, and then subtract back once the contributions of the real modes,
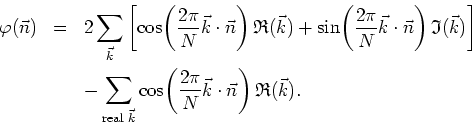
This second sum runs over only either ![]() or
or
![]() elements, depending on the parity of
elements, depending on the parity of ![]() , and is
therefore much smaller than the first one, which runs over
, and is
therefore much smaller than the first one, which runs over ![]() elements, specially for large lattices, representing therefore only a
small additional computational effort. In order to do this it will be
necessary to construct a small indexing array to pick the purely real
modes out of the indexed vector of modes. Note that the first term of the
inverse transformation matrix
elements, specially for large lattices, representing therefore only a
small additional computational effort. In order to do this it will be
necessary to construct a small indexing array to pick the purely real
modes out of the indexed vector of modes. Note that the first term of the
inverse transformation matrix
![]() , as decomposed
above, is equal to
, as decomposed
above, is equal to
![]() . In order to deal with the second
term, consider an indexing array
. In order to deal with the second
term, consider an indexing array
![]() of dimension
of dimension
![]() , which for each
, which for each
![]() , with
, with
![]() for odd
for odd ![]() and
and
![]() for even
for even ![]() , returns
the value of the index
, returns
the value of the index ![]() of a purely real mode. Using it we can
write the inverse transform as
of a purely real mode. Using it we can
write the inverse transform as
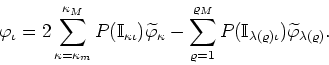
We have therefore the inverse transformation implemented by a large
matrix operation followed by a small correction, which is still easy to
implement efficiently. In the computer code we will actually have two
indexation matrices
![]() and
and
![]() , differing only by the
ordering of the indices, one for the direct transformation and one for
the inverse transformation, so that both can be executed efficiently.
, differing only by the
ordering of the indices, one for the direct transformation and one for
the inverse transformation, so that both can be executed efficiently.